Асимптоты графика функции

Мы продолжаем изучать инструменты построения графика функции как наиболее удобного представления характера зависимости одной переменной от другой. При исследовании поведения функции на бесконечности (т.е. при и ) или вблизи точек разрыва второго рода часто оказывается, что график функции сколь угодно близко приближается к некоторым характерным прямым. Такие прямые называются асимптотами графика функции. Понятно, что если бы мы научились находить такие прямые, то это нам очень бы помогло для более точного построения графика. Прямые на координатной плоскости могут быть вертикальными (параллельными оси у) и наклонными (в частности, горизонтальными). В зависимости от того, к какой из них приближается график функции, будем различать вертикальные и наклонные асимптоты.

И зучим сначала наклонные асимптоты. Как видно из рисунка, график функции может приближаться к различным прямым при и . Поэтому различают наклонные асимптоты при и наклонные асимптоты при . Исходя из геометрических представлений, дадим определение наклонной асимптоты при . Любая наклонная прямая имеет, как известно, уравнение вида . Меняя числа и , получим уравнения всех наклонных прямых. При некоторой паре чисел и может получиться интересующая нас асимптота при . Если мы найдем формулы для нахождения этих чисел, то научимся находить уравнение асимптоты, по которому сможем построить и саму асимптоту. Прежде всего нужно дать строгое определение асимптоты. Пока мы просто высказали желание уметь находить прямые, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Но фраза, заключенная в кавычках, ни коим образом не может являться строгим математическим определением, с которым можно «работать» математическими средствами. Поэтому попробуем дать строгое определение асимптоты, исходя из того, какое свойство графика мы хотим описать этим понятием. Итак, пусть прямая с уравнением является наклонной асимптотой графика функции при , т.е. к ней «бесконечно близко примыкает график функции при удалении точки графика в бесконечность» (см. рисунок ). Пусть − текущая точка на оси (мы потом устремим ). Длина отрезка есть не что иное, как значение функции в точке , т.е. . Поскольку точка лежит на асимптоте с уравнением , то длина отрезка есть значение функции в текущей точке , т.е. . Поэтому длина отрезка . По рисунку расстояние от точки графика до асимптоты (которое и должно по нашему мнению стремиться к 0 при ): при . Из прямоугольного треугольника находим . Поэтому при только в том случае, когда стремится к 0 при . Исходя из этого, можно принять следующее определение. Наклонная прямая с уравнением называется наклонной асимптотой графика функции при , если

(1) .

Вот это уже вполне математически корректное определение. Аналогично определяется наклонная асимптота при : прямая с уравнением называется наклонной асимптотой графика функции при , если

(2) .

Т еперь, после введения строгого определения, вернемся к вопросу о нахождении формул для чисел и в уравнении асимптоты . Справедлива следующая

Теорема. Для того, чтобы график функции имел наклонную асимптоту при с уравнением необходимо и достаточно, чтобы существовали два предела: , .

Докажем, например, необходимость. Пусть прямая является асимптотой графика функции при . Требуется доказать, что , . Поскольку прямая является асимптотой графика функции при , то по определению (1) выполняется: . Преобразуем: (приводя правую часть к общему знаменателю мы как раз получим левую часть). Переходя к пределу в левой и правой части этого равенства, получим 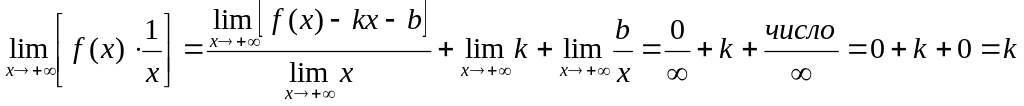. Первое из требуемых равенств получили. Получим второе. Представим . Переходим к пределу в левой и правой части: . Что и требовалось доказать.

Итак, коэффициенты уравнения наклонной асимптоты графика функции при находятся по формулам:

(3) , .

Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при у графика нет.

Что касается наклонной асимптоты при , то для нее можно повторить все, что сказано для наклонной асимптоты при , но во всех пределах надо заменить на . В частности, коэффициенты уравнения наклонной асимптоты графика функции при находятся по формулам , . Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при у графика нет. При поиске наклонных асимптот графика необходимо искать уравнение обеих асимптот (при и ). Но для одного класса функций в этом необходимости нет. Доказано, что если функция представляет собой отношение двух многочленов, то ее асимптоты (если они есть) при и совпадают. В этом случае асимптота, найденная при будет являться и асимптотой при .

П ерейдем теперь к изучению вертикальных асимптот, т.е. вертикальных прямых, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Попробуем снова дать математическое определение вертикальной асимптоте. Любая вертикальная прямая имеет уравнение вида , где − то число, в котором вертикальная прямая пересекает ось х. Допустим, что такая прямая является вертикальной асимптотой. Для бесконечно близкого приближения графика к такой прямой необходимо, чтобы график хотя бы с одной стороны от этой прямой при подходе к ней резко шел вверх или вниз. Других вариантов нет. Один из возможных вариантов приведен на рисунке. Что же означает такое поведение графика? Если мы начнем приближаться значениями к числу с правой стороны (как при вычислении правого предела) и каждый раз по графику будем следить за соответствующими значениями функции (см. рисунок), то видно, что значения функции стремятся к +∞. Это означает, что правый предел . Аналогично, можно показать, что для функции, график которой изображен на рисунке, левый предел . Бесконечность (+ или −) хотя бы одного такого одностороннего предела и означает безграничное приближение графика к вертикальной прямой с уравнением хотя бы с одной стороны. То есть то, что мы и хотели от вертикальной асимптоты. Поэтому естественно принять следующее определение вертикальной асимптоты. Прямая с уравнением называется вертикальной асимптотой графика функции , если выполняется хотя бы одно из условий: или . Поэтому для доказательства того, что некоторая прямая с уравнением является вертикальной асимптотой, необходимо считать такие пределы. Если хотя бы один из них равен или , то прямая есть вертикальная асимптота. Иначе − нет. Как же все-таки находить вертикальные асимптоты графика заданной функции ? Невозможно же для каждого числа на числовой оси х считать оба односторонних предела, чтобы понять, будет ли проходящая через это число вертикальная прямая являться вертикальной асимптотой. Необходимо как-то ограничить количество точек на оси х, подозрительных на прохождение через них вертикальных асимптот. Из приведенного определения вертикальных асимптот следует, что если прямая с уравнением есть вертикальная асимптота, то точка обязательно есть точка разрыва функции , причем второго рода (односторонние пределы бесконечны). Поэтому проверять нужно только точки разрыва функции. У нас было (при изучении непрерывности функции), что если функция задана одной формулой (т.е. является элементарной функцией), то она непрерывна в точках области определения, а потому точки ее разрыва лежат на границе области определения. Поэтому получаем следующее правило: проверять на вертикальные асимптоты графика функции можно только такие прямые с уравнением , у которых число лежит на границе области определения функции. Напомним, что граничными точками некоторого множества называются такие точки, в любой окрестности которых есть точки как принадлежащие этому множеству, так и ему не принадлежащие. Поэтому упомянутые выше граничные точки области определения функции это точки, в любой окрестности которых есть как точки области определения функция, так и точки, в нее не входящие.

Пример 1. Найти асимптоты графика функции .

Решение.

1) Находим наклонные асимптоты. Вычисляем и для наклонной асимптоты при по формулам (1):

. Итак, . Далее,

. Итак, . Поэтому уравнение наклонной асимптоты при : . Поскольку исследуемая функция представляет собой отношение двух многочленов (второй и первой степени), то, как сказано выше, эта же прямая будет наклонной асимптотой и при .

2) Найдем вертикальные асимптоты. Их уравнение имеет вид , причем (по приведенному выше правилу) число может лежать только на границе области определения функции. Поскольку область определения функции есть , то граничной точкой такой области является только число 0, поскольку в любой окрестности этой точки есть точки как из области определения, так и не из нее (это сама точка 0). Поэтому проверяем только . Это значит, что проверяется на вертикальную асимптоту прямая с уравнением (эта прямая, как известно, совпадает с осью у). Считаем односторонние пределы при : . Дробь означает, что при подстановке вместо числа 0 в числителе получается число , а в знаменателе 0, к которому пришли со стороны положительных чисел. При изучении псевдонеопределенностей мы получали, что . Осталось понять, почему мы поставили знак минус у этой бесконечности. При , близких к 0 со стороны положительных чисел, выяснилось, что числитель приближается к числу (т.е. становится отрицательным), а знаменатель положителен. Поэтому вся дробь под знаком предела отрицательна. Поэтому получилась именно (−∞). Аналогично получаем для левого предела . Итак, получили , . Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением (т.е. ось у) является вертикальной асимптотой. На рисунке схематично изображен график исследуемой функции, видно поведение графика вблизи асимптот.

Пример 2. Найти асимптоты графика функции .

Решение. Прежде всего, найдем область определения, которая в данном примере играет существенную роль. Поскольку в правой части формулы переменная встречается под знаком логарифма, то она должна быть строго положительной: . С другой стороны, при вычислении значения функции присутствует операция деления на . Поскольку на 0 делить нельзя, то исключаем из возможных значение . Таким образом, область определения данной функции − все положительные числа, за

исключением числа 3, т.е. объединение двух интервалов: . Поскольку (как мы только что выяснили) не может принимать отрицательные значения, то это означает, что над отрицательной частью оси график этой функции вообще отсутствует, а потому у него (графика то есть) не может быть никакой асимптоты при . Далее двигаемся по схеме решения предыдущего примера.

1) Вычисляем и для наклонной асимптоты при по формулам (1): . Осталось вычислить: {применяем правило Лопиталя} . Поэтому из предыдущей формулы . Далее, (то, что , как и выше легко доказывается по правилу Лопиталя). Итак, , , а потому уравнение наклонной асимптоты при : . Как было показано выше, наклонной асимптоты при у графика данной функции нет.

2) Найдем вертикальные асимптоты. Их уравнения имеют вид , причем (по приведенному выше правилу) число может лежать только на границе области определения функции, т.е. на границе числового множества . Граница этого множества состоит только из двух чисел: 0 и 3. Поэтому возможны только случаи и , а потому вертикальными асимптотами могут быть только прямые с уравнениями и . Рассмотрим сначала случай . Это значит, что проверяется на вертикальную асимптоту прямая с уравнением (это снова ось у). Считаем односторонние пределы при . Поскольку найденная выше область определения функции не содержит отрицательных чисел, то мы не сможем вычислить левый предел данной функции при , поскольку при этом пришлось бы приближаться к 0 со стороны отрицательных чисел, в которых значения функции не определены, а потому и не могут приближаться ни к какому числу. Считаем правый предел функции при : . Вычислим получившийся предел: . Если вспомнить поведение графика функции , то будет ясно, что при приближении к нулю (со стороны положительных чисел) становится отрицательным и стремиться к . Выражение же будет при этом, очевидно, тоже отрицательным, приближаясь к числу . Таким образом, вся дробь будет положительной, а потому . Окончательно получаем: . Таким образом, оказалось, что один из односторонних пределов (в данном случае правый) оказался бесконечным. Поэтому по определению прямая с уравнением (т.е. ось у) действительно является вертикальной асимптотой графика исследуемой функции.

Рассмотрим оставшийся случай . Это значит, что проверяется на вертикальную асимптоту прямая с уравнением (вертикальная прямая, проходящая через число 3 на оси ). Считаем односторонние пределы при . Считаем правый предел: . Вычислим получившийся предел: (вспомните псевдонеопределенности при вычислении пределов). Определим знак получившейся бесконечности. При приближении к числу 3 справа (т.е. при этом остается больше, чем 3) числитель приближается к положительному (подумайте, почему?) числу , а потому сам становится положительным. Знаменатель дроби тоже положителен, так как выше уже отмечено, что остается больше, чем 3. Таким образом, вся дробь под знаком предела положительна, а потому . Итак, .

Аналогично считаем левый предел: . Вычислим получившийся предел: . Определим знак получившейся бесконечности. При приближении к числу 3 слева (т.е. при этом остается меньше, чем 3) числитель снова приближается к тому же положительному числу , а потому сам становится положительным. Знаменатель дроби теперь уже отрицателен, так как выше уже отмечено, что остается меньше, чем 3. Таким образом, вся дробь под знаком предела отрицательна, а потому . Итак, . Поскольку оба односторонних предела оказались бесконечными, то прямая с уравнением тоже является вертикальной асимптотой графика исследуемой функции.

Ответ: График функции имеет одну наклонную асимптоту при с уравнением и две вертикальных асимптоты с уравнениями (ось у) и .