Направление выпуклости графика функции и точки перегиба

График функции лучше всего характеризует характер зависимости некоторого фактора от другого фактора , задаваемой этой функцией. На графике сразу видно, где функция возрастает, а где убывает и насколько быстро, сразу видны ее экстремумы, интервалы положительности и отрицательности ее значений и т.д. . Чего не скажешь, глядя на саму формулу , которой задается функция. Поэтому конечной целью исследования функции обычно является построение ее графика. Исследование функции на монотонность и экстремум (пройденное выше) значительно облегчает построение графика функции и в дальнейшем войдет в общую схему исследования функции и построения ее графика. Однако есть еще некоторые инструменты исследования ф ункции, помогающие достаточно точно строить ее график. Рассмотрим некоторую функцию . Допустим, что мы при исследовании ее на монотонность установили, что на некотором интервале функция возрастает . Это означает, что при рисовании графика должны вести его строго вверх между точками А и В ( с координатами и ). Но сделать это можно по-разному (см. рисунок): либо провести график выпуклостью вверх или вниз. Как же определить направление выпуклости. Первая производная (которая указала нам просто на возрастание функции) ответа уже не даст. В данном случае ответ даст уже вторая производная. Сначала заметим (по рисунку), что если кривая имеет выпуклость вверх, то она расположена под касательной, проведенной к любой из ее точек. А если выпуклость направлена вниз, то над касательной. Поэтому примем такие определения. Будем говорить, что график функции имеет на интервале выпуклость, направленную вверх (вниз), если он расположен н иже (выше) любой касательной к графику функции на . Обозначается выпуклость вверх (вниз) на интервале так: Каким же образом вторая производная покажет направление выпуклости графика? Обратимся к рисунку, на котором график функции имеет на интервале выпуклость вверх. Возьмем произвольные точки и из такие, что . Построим касательные в соответствующих точках графика (на рисунке). Пусть касательная в точке графика с координатой образует с осью угол , а касательная с координатой угол . Из геометрического смысла производной ясно, что , а . Из рисунка видно, что при выпуклости графика вверх угол меньше угла , а потому и , т.е. . Таким образом, выяснено, что большему значению х соответствует меньшее значение функции . Это (по определению) означает, что функция убывает на интервале . Тогда по пройденному признаку убывания функции ее производная (т.е. ) должна быть отрицательной на этом интервале. Но по определению производная от производной и есть вторая производная : . Итак, мы доказали (точнее, показали), что если график функции имеет на некотором интервале выпуклость вверх, то вторая производная этой функции (если она, конечно, существует) является отрицательной (точнее, неположительной). Аналогично можно доказать-показать, что если график функции имеет на некотором интервале выпуклость вниз, то его вторая производная положительна (точнее, неотрицательна). Итак, справедлива

Теорема. Пусть у функции существует на вторая производная . Тогда если ( ) на , то график функции имеет на этом интервале выпуклость вниз (вверх).

Таким образом, мы выяснили, что направление выпуклости графика функции определяется знаком ее второй производной.

Прейдем теперь к так называемым точкам перегиба графика. Ранее точки экстремума (максимумы и минимумы) обычно разделяли участки монотонности функции разного вида (возрастание − убывание, убывание − возрастание). Аналогично, участки графика, имеющие разное направление выпуклости, тоже обычно разделяются некоторой характерной точкой графика, которая называется точкой перегиба (см. рисунок). Дадим определение такой точки. Точка графика функции называется точкой перегиба , если выполнены условия:

а) существует касательная к графику в этой точке;

б) по разные стороны от этой точки график имеет разные направления выпуклости.

Т ребование существования касательной в точке перегиба продиктовано тем, что в точке перегиба переход от одного направления выпуклости к другому должен проходить «гладко» (перегиб, а не перелом). Отсутствие касательной, как было сказано раньше, ведет к появлению точки излома графика. Такая точка не считается точкой перегиба, даже если она действительно разделяет разные направления выпуклости графика (такова точка на рисунке слева). Если в точках экстремума (первая) производная функции (если она существует) обращается в 0, то в точках перегиба должна обращаться в 0 вторая производная функции (если она тоже существует). Это выражает следующая

Теорема (необходимое условие точки перегиба) . Пусть в точке существует и непрерывна вторая производная функции и − точка перегиба ее графика. Тогда .

Таким образом, абсциссы (т.е. -координаты) точек перегиба надо искать среди точек, в которых вторая производная обращается в 0 или не существует. Фактически это критические точки для первой производной. Дадим название таким точкам. Точки, в которых вторая производная функции обращается в ноль или не существует, называются критическими точками функции второго рода. Вывод: -координаты точек перегиба находятся только среди критических точек 2 рода. Однако не все такие точки (т.е критические точки 2 рода) обязательно соответствуют точкам перегиба. В качестве примера рассмотрим функцию . Ее график имеет ту же форму, что и парабола , но ветви у него круче идут вверх (см. рисунок). Точек перегиба у него нет, так как ее график имеет выпуклость вниз на всей числовой прямой (ее вторая производная равна , а потому везде положительна). Однако ясно, что вторая производная обращается в 0 при , а потому есть критическая точка 2 рода. Но соответствующая ей точка графика − начало координат − не точка перегиба. Поэтому для исследования произвольных функций опять нужен алгоритм, позволяющий отсеивать критические точки функции 2 рода, не дающие перегиб. Такой алгоритм прост и нагляден.

Т еорема (достаточное условие точки перегиба). Пусть функция имеет вторую производную в некоторой окрестности точки . Тогда если в пределах указанной окрестности эта производная имеет разные знаки слева и справа от точки , то график функции имеет перегиб в точке .

Доказательство очевидно, так как разные знаки второй производной означают разное направление выпуклости справа и слева от .

Замечание. Теорема остается верной и при более слабых условиях. Условие существования второй производной в окрестности точки (включая ее саму) можно заменить наличием второй производной в выколотой окрестности этой точки (т.е. без самой точки ) и наличием касательной к графику в точке (т.е. существованием производной в самой точке ).

Итак, вопрос о направлении выпуклости и точках перегиба решается с помощью второй производной.

Пример 1. Исследовать график функции на выпуклость и точки перегиба.

Решение. Мы уже ранее исследовали эту функцию на монотонность и экстремумы. Ищем критические точки 2 рода. Находим первую и вторую производную: , . Вторая производная существует на всей числовой прямой и обращается в 0 только при (критическая точка функции 2 рода), причем . Поэтому − единственная точка графика функции, подозрительная на точку перегиба этого графика. По аналогии с исследованием ф ункции на монотонность и экстремумы наносим точку на числовую прямую и исследуем знаки второй производной на получившихся интервалах. Очевидно, что при и при . Поэтому и . Точка разделяет интервалы разных знаков для второй производной, а сама она в этой точке обращается в 0. Поэтому по теореме о достаточном условии точки перегиба критическая точка графика является точкой перегиба.

П ример 2. Исследовать график функции на выпуклость и точки перегиба.

Решение. Ищем критические точки 2 рода. Находим производную (чтобы найти потом вторую производную): . Тогда вторая производная: . Она существует на всей числовой прямой и обращается в 0 только при (так как функция не обращается в 0 ни при каких значениях , оставаясь все время положительной). Итак, − единственная критическая точка функции 2 рода, причем . Поэтому − единственная точка графика функции, подозрительная на точку перегиба. Наносим точку на числовую прямую и исследуем знаки второй производной на получившихся интервалах. Поскольку экспонента положительна при любых , то очевидно, что при и при . Поэтому и . Точка разделяет интервалы разных знаков для второй производной. Поэтому по теореме о достаточном условии точки перегиба точка графика действительно является точкой перегиба.

П ример 3. Провести аналогичное исследование для функции . Решение. Ищем критические точки 2 рода. Первая производная: . Тогда вторая производная: 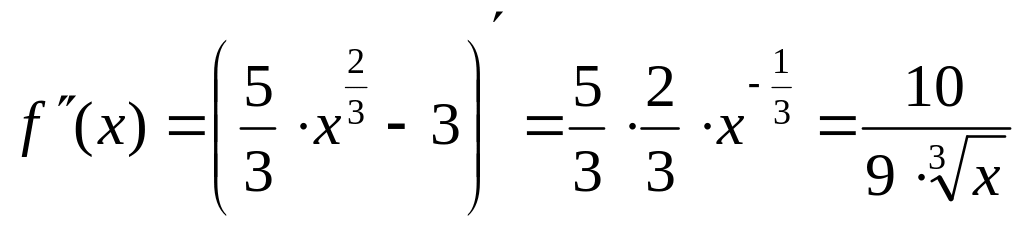. Она не существует только при (на ноль делить нельзя), а потому является критической точкой 2 рода. Других критических точек нет, поскольку ни при каких значениях не обращается в 0 ( дробь может обратиться в 0 только если ее числитель равен 0, а у нас в числителе стоит число 10, которое ни при каких другим не станет). Итак, − единственная критическая точка функции 2 рода, причем . Поэтому − единственная точка графика функции, подозрительная на точку перегиба. Наносим точку на числовую прямую и исследуем знаки второй производной на получившихся интервалах. Из приведенного выражения для второй производной очевидно, что при и при . Поэтому и . Точка разделяет интервалы разных знаков для второй производной, но вторая производная не существует при . Однако она существует в любой выколотой окрестности этой точки, а в самой точке существует первая производная . Поэтому по замечанию к теореме о достаточном условии точки перегиба точка графика является точкой перегиба.