Правило Лопиталя вычисления пределов

Мы начинаем изучать приложения понятия производной. Основные приложения (о них мы будем говорить позже) производной функции состоят в том, что эта производная помогает изучить характер зависимости переменной от переменной , выраженный видом самой функции . Однако производная дает еще и мощный универсальный метод раскрытия неопределенностей в пределах. Когда мы проходили эту тему, то давали лишь немногие приемы, помогающие избавиться от неопределенности в некоторых частных случаях. Каждый из этих приемов «работал» лишь для одного из типов неопределенности, причем для достаточно узкого набора функций под знаком предела.

Пусть необходимо вычислить предел отношения двух функций , который при подстановке в эту дробь значения вместо в дробь дает неопределенность. Обычно в этом случае возникает неопределенность типа или . В этом случае правило Лопиталя говорит о том, что вместо предела отношения исходных функций и можно считать предел отношения их производных и . Это уже будут другие функции, поэтому предел их отношения возможно неопределенности и не даст, мы сможем его вычислить обычной подстановкой вместо в выражение под знаком предела. Тогда полученное при этом значение и будет значением исходного предела:

(1) .

Если же предел справа в (1) опять дает неопределенность, то правило Лопиталя применяется уже к этому пределу . И так до тех пор, пока неопределенность не исчезнет.

Для полноты изложения приведем строгую формулировку теоремы, выражающей правило Лопиталя, хотя для практического его применения в большинстве случаев достаточно запомнить только формулу (1).

Теорема. Пусть

1) функции и определены и дифференцируемы в некоторой окрестности точки (за исключением, быть может, самой точки );

2) в указанной окрестности;

3) и либо и ( а потому при вычислении реально возникает неопределенность ) ;

4) существует (конечный или бесконечный) предел отношения производных . Тогда существует и исходный предел , причем справедлива формула (это и есть формула (1) ).

Замечание. Правило Лопиталя остается справедливым, если в (1) или . Справедливо оно и для случая односторонних пределов , если или .

Интересно, что правило Лопиталя гарантированно работает только в случае возникновения неопределенности. Иначе оно может дать неверный результат. Например, очевидно, что , однако . Поэтому правило Лопиталя (1) для данного примера не работает, поскольку изначально в пределе неопределенности нет, а потому он может быть вычислен простой подстановкой (что и было сделано).

Итак, перед применением правила Лопиталя (1) необходимо проверить наличие неопределенности. Если ее нет, то предел вычисляется обычной подстановкой вместо в выражение под знаком предела. Если же есть, то применяется правило Лопиталя. Рассмотрим примеры.

Пример 1. = = = .

Пример 2. .

Пример 3. ={снова применяем правило Лопиталя} .

Пример 4. = = = .

Пример 5. = = .

Пример 6. = = = ={вспоминаем первый замечательный предел: } . Пример 7. .

Однако неопределенности в пределах возникают не только если под знаком предела стоит отношение двух функций, да и список возможных неопределенностей не сводится только к или (неопределенности могут быть вида , , , , ) . Как же раскрывать неопределенность в этих случаях? Поскольку правило Лопиталя (1) применимо только к отношению двух функций с определенным видом неопределенности, то выход один. В этих случаях необходимо так тождественно преобразовать выражение под знаком предела, чтобы оно приняло вид отношения двух функций с неопределенностью или . Как проводятся такие преобразования, будет ясно из следующих примеров.

Пример 8. {предел односторонний, так как х, будучи под знаком логарифма, не может принимать отрицательные значения} {для приведения пределу к виду, удобному для применения правила Лопиталя, перенесем х в знаменатель, но, естественно, как } {применяем правило Лопиталя} .

Пример 9.

.

Неопределенности вида , , возникают в пределах вида , когда основание и показатель степени стремятся к соответствующим значениям. Свести такой предел к виду, для которого можно применить правило Лопиталя (1) , помогает следующий прием. Несложно понять (или вспомнить), что для любых чисел и справедливо (из основного логарифмического тождества) представление степени в виде : . Поэтому . Допустим, что мы выяснили, к чему стремится полученный показатель степени : . Тогда (из непрерывности функции ) получим: .

Пример 10. . Это следует из того, что выше с помощью правила Лопиталя было вычислено .

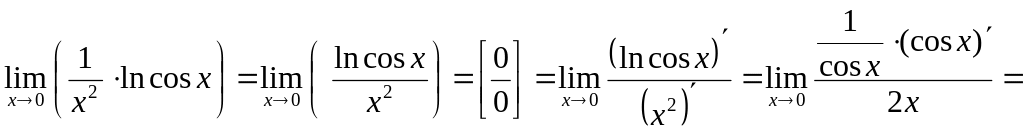
Пример 11. . Остается вычислить предел показателя степени: (последний из пределов – первый замечательный предел). Поэтому исходный .