Правила нахождения производных. Таблицы производных
Выше, используя определение, была вычислена производная только функции . Точно таким же образом, исходя из определения производной, можно вычислить производные и от других известных функций. Результаты сведены в следующую простую таблицу производных :
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
Первая формула в таблице говорит о том, что если функция равна постоянному числу (или, как говорят, функция является константой), то ее производная в любой точке равна 0. В формуле (под номером 3 в таблице производных) показатель степени может быть любым: целым положительным, целым отрицательным, дробным положительным, дробным отрицательным. Рассмотрим примеры применения этой формулы при различных типах показателя степени . Первый пример – показатель степени является целым и положительным.
Пример 1.
{
− целое положительное}
.
В следующем примере
показатель степени − целое отрицательное
число. Сначала напомним определение
отрицательного показателя степени:
.
Нам понадобится это равенство справа
налево:
.
Пример 2.
{
− целое отрицательное}
.
Дальше показатель
степени − дробное положительное число.
Напомним определение степени с дробным
показателем:
. Нам снова понадобится это равенство
в обратном порядке:
.
Пример 3.
{
− дробное положительное} =
.
Последний случай : показатель степени − дробное и отрицательное число.
Пример 4.
{
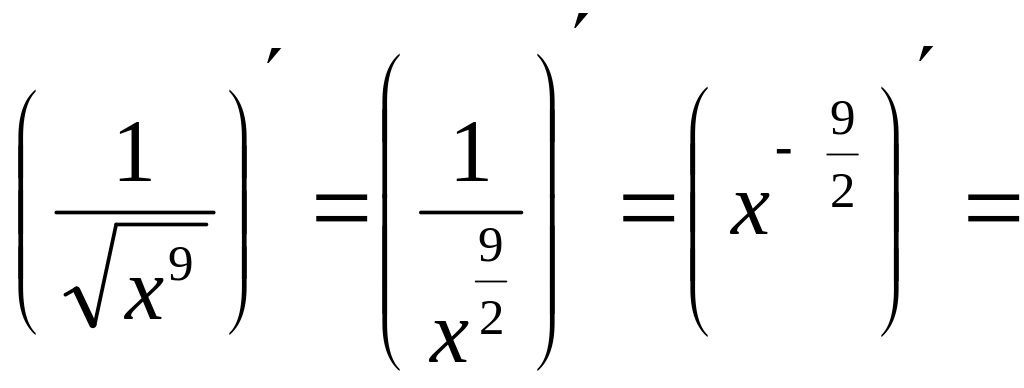− дробное отрицательное} =
.
Итак, пока мы умеем
вычислять производные только от функций,
перечисленных в таблице. А если формула,
задающая функцию, содержит суммы,
разности, произведения и частные от
функций, содержащихся в этой таблице?
Или содержит суперпозиции перечисленных
функций (т.е. функции от функций, например,
) ? Для вычисления
производных в этом случае используются
правила, которые дает следующая
Теорема.
1.
Пусть функции
и
дифференцируемы в точке
(т.е. имеют производную в этой точке)
, а а
− некоторое число. Тогда в этой точке
дифференцируемы и функции
(если
),
а их производные вычисляются по правилам:
а) постоянный множитель можно выносить за знак производной :
(1)
б) производная суммы-разности равна сумме-разности производных:
(2)
в) для производной от произведения аналогия не проходит :
(3)
г) наиболее громоздкая формула − для производной от частного (т.е. дроби):
(4)
2.
Пусть функция
дифференцируема на некотором интервале
,
а функция
дифференцируема
на области значений функции
.
Тогда сложная функция (или суперпозиция
функций)
дифференцируема на интервале
, а ее
производная вычисляется по формуле:
.
Кратко эта формула записывается в виде:
(5)
Для того чтобы
было удобнее пользоваться формулой
для дифференцирования (т.е. взятия
производной) сложной функции, эта
формула сразу применена ко всем функциям,
составляющим выписанную выше таблицу
производных. В применении к таблице
производных эта формула говорит о том,
что если в таблице производных в левой
части вместо
стоит любое более сложное выражение
(функция
),
то в правой части равенств нужно тоже
поставить выражение
вместо
,
а потом еще домножить эту правую часть
на производную от
, т.е.
.
Результаты
такого применения выписаны следующей
таблице, которая называется обобщенной
таблицей производных
(сравните с простой таблицей производных)
:
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
Теперь при вычислении
производных от различных функций можно
практически забыть о формуле для
производной сложной функции, а пользоваться
только простой или обобщенной таблицей
производных, руководствуясь следующим
правилом: если под знаком функции
(синуса, косинуса, логарифма и т.д.) стоит
сам аргумент
,
то для вычисления производной надо
использовать простую таблицу производных,
а если же под знаком функции стоит более
сложное выражение (представляющее собой
некоторую формулу от
),
то это выражение надо принимать за
функцию
и пользоваться обобщенной таблицей
производных до тех пор, пока аргументы
не упростятся, после чего опять будет
окончательно использоваться простая
таблица. Если в обобщенной таблице
производных положить
,
то она перейдет в простую таблицу
производных. Простая и обобщенная
таблицы производных, а также правила
вычисления производных от суммы,
разности, произведения и частного
(сформулированные в теореме) позволяют
вычислять производную от функции,
заданной сколь угодно сложной формулой.
Надо только набраться опыта в их
практическом применении. А опыт
появляется только после решения примеров
и задач.
Пример 5
.
{формула 7 обобщенной таблицы производных}
{формула 9 простой таблицы производных}=
.
Пример 6
.
{формула
8 обобщенной таблицы производных}
{формула
5 обобщенной таблицы производных}
{формула
9 простой таблицы производных}
.
Пример 7
.
.
Найти производную
.
Решение.
{правило
(2) для производной от суммы-разности}
{правило (1) − вынесение числового
множителя за знак производной}
{формулы
2 и 3 простой таблицы производных}
=
.
Пример 8
.
.
Найти производную
.
Решение.
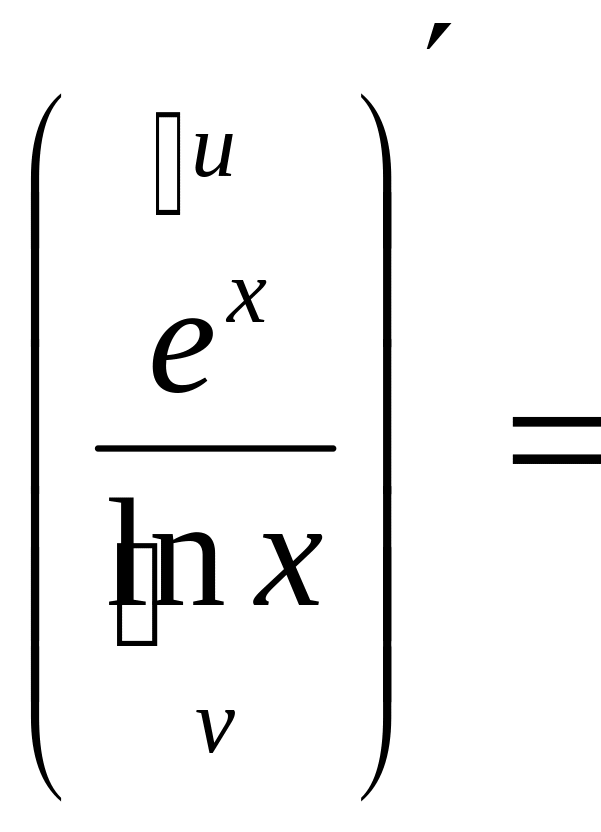{правило
(4) для производной от частного}=
{формулы
5 и 7 простой таблицы производных}=
.
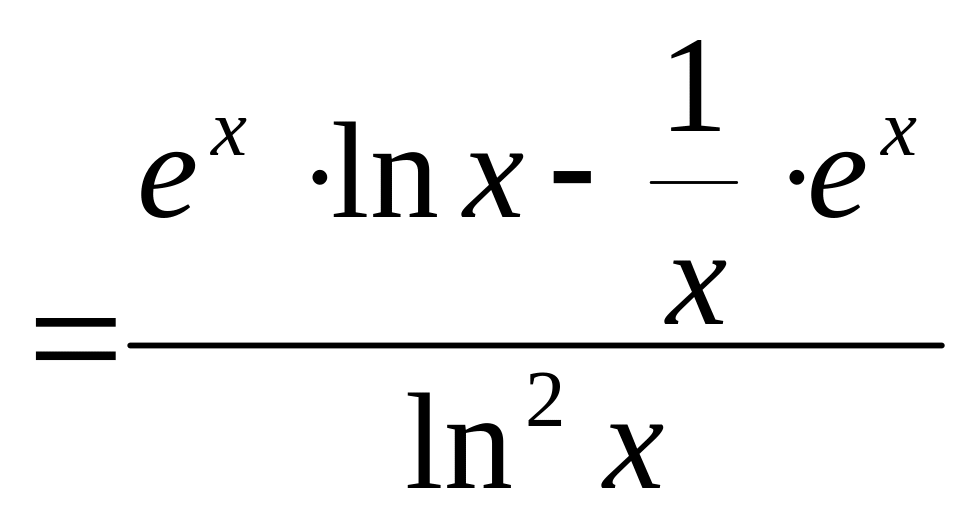Пример 9
.
.
Найти производную
.
Решение.
{определение
дробной и отрицательной степени}=
{правило
(3) для производной произведения}=
{формула (3) из простой и (5) из обобщенной
таблицы производных}=
.
Пример 10
.
{определение
тангенса}
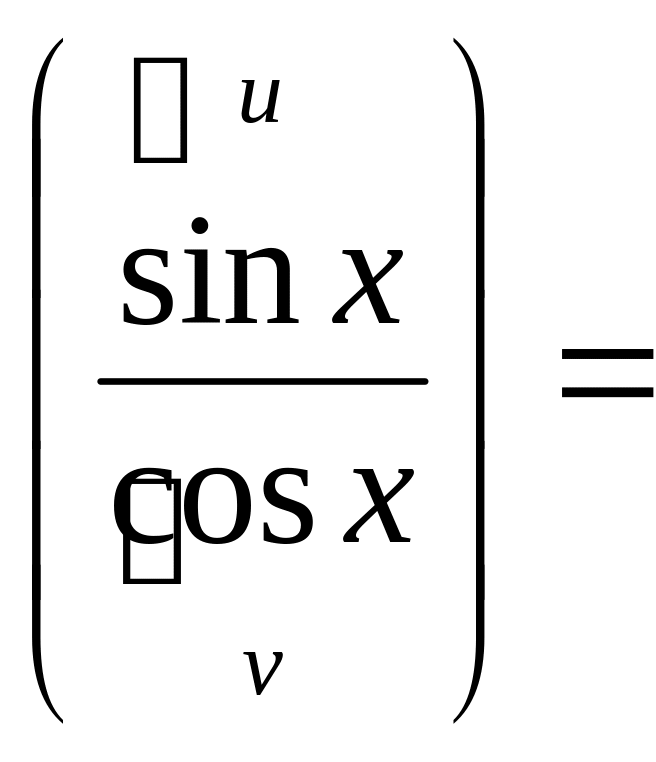{правило
(4) для производной от частного}
.