Точки разрыва функции

Перейдем к изучению так называемых «точек разрыва» функции. Вспомним, что по определению точка (в окрестности которой задана функция ), называется точкой непрерывности данной функции, если выполнено: или (что то же самое, но теперь более удобное для нас) . Естественно принять следующее определение. Точка называется точкой разрыва функции , если она не является точкой непрерывности этой функции, т.е. в этой точке нарушается хотя бы одно из следующих условий (которые в совокупности и составляли условие непрерывности функции):

1. Существуют оба односторонних предела и , причем , . 2. 3.

Классификация точек разрыва функции

В зависимости от того, какое из перечисленных выше условий непрерывности функции нарушается, точки разрыва классифицируются различным образом.

1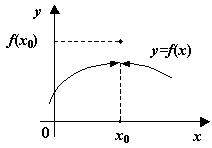 . Пусть нарушено только третье условие непрерывности. Это значит, что существуют оба односторонних предела и , , но . То есть значение функции не совпадает с одинаковыми предельными ее значениями справа и слева. В этом случае точка называется точкой устранимого разрыва функции . Типичная ситуация для этого случая изображена на рисунке. Стоит нам изменить значение функции в точке (положив ), как функция станет непрерывной в этой точке (устранение разрыва).

Пример 1. Исследовать на непрерывность функцию . Решение. Функция определена на всей числовой прямой и задана двумя формулами, а потому на подозрении в отсутствии непрерывности может быть только точка стыка различных формул . Исследуем функцию на непрерывность в этой точке. Посчитаем односторонние пределы и при . Вспоминая первый замечательный предел, получаем, что и . Таким образом, оба односторонних предела совпадают: , но . В этом случае точка по приведенной выше классификации является точкой устранимого разрыва. Таким образом, заданная функция непрерывна на всей числовой прямой, за исключением точки , которая является точкой устранимого разрыва. Заметим, что если изменить значение функции всего в одной точке и задать ее выражением , то она станет непрерывной на всей числовой прямой (устранение устранимого разрыва).

2 . Пусть первое условие непрерывности не нарушено (т.е. существуют оба односторонних предела и , причем , ), но нарушено второе (а потому, автоматически, и третье) условие, т.е. . В этом случае точка х₀ называется точкой разрыва первого рода (или скачком ), а число называют величиной скачка. Типичная картина скачка (в точке ) показана на рисунке.

Пример 2: Исследовать на непрерывность функцию:

.

Решение. Найдем область определения этой функции. При всех функция определяется верхней формулой. Для всех таких чисел выражение под знаком логарифма положительно, а потому все они входят в область определения функции. Для всех вычисление функции по нижней формуле тоже не вызывает никаких трудностей. Поэтому область определения заданной функции – вся числовая прямая. Тогда из Правила 2 в параграфе «Свойства функций, непрерывных в точке» следует, что, поскольку функция определяется двумя формулами и определена для всех чисел , то она непрерывна на всей числовой прямой, кроме, быть может, точки (точка стыка двух формул). Исследуем на непрерывность точку . Вычисляем односторонние пределы:

{поскольку при вычислении левого предела мы приближаемся числами к 2 слева (т.е. со стороны чисел, которые меньше 2), то под знаком предела в качестве должна фигурировать верхняя формула, задающая для } = = = , то есть . Далее, , то есть . Поскольку , то точка разрыва первого рода ( скачок ). Величина скачка .

3. Если нарушено первое условие непрерывности, т.е. хотя бы один из односторонних пределов не существует или равен ∞ (т.е. А = ± ∞ или В = ± ∞ ), то точка называется точкой разрыва второго рода (или бесконечный скачок ).

Пример 3: Исследуем на непрерывность функцию . Ее график (гипербола) изображен на рисунке. Поскольку функция задана одной формулой, то она непрерывна во всех точках, кроме, быть может, , которая не принадлежит ее области определения. Исследуем точку . Вычисляем левый и правый пределы (такие односторонние пределы выше уже вычислялись): , т.е. . Далее, , т.е. . Поэтому − точка разрыва второго рода ( бесконечный скачок ). Соответствующее поведение графика этой функции вблизи точки разрыва изображено на рисунке.

Рассмотрим примеры на тему непрерывности функции.

Пример 4. Исследовать на непрерывность функцию .

Решение. Функция определена при всех (при знаменатель обращается в 0). Поскольку она задана одной формулой, то (по Правилу 1 в параграфе «Свойства функций, непрерывных в точке» ) она непрерывна на всей числовой прямой, за исключением, быть может, точки 1. Исследуем отдельно на непрерывность-разрывность точку . Вычисляем односторонние пределы:

. Если помните, когда при вычислении предела после подстановки вместо его предельного значения получается , то это было названо псевдонеопределенностью и давало бесконечность. Знак этой бесконечности определяется знаком функции . При приближении к 1 числитель этой дроби становится положительным, так как приближается к положительному числу 1. Поскольку приближается к 1 слева (т.е. со стороны чисел, которые меньше 1), то и знаменатель этой дроби тоже становится положительным. Таким образом, дробь приближается к бесконечности, оставаясь положительной. Поэтому . Аналогично, легко получить, что правый предел (при приближении к 1 справа знаменатель становится отрицательным). По приведенной выше классификации есть точка разрыва 2 рода.

Пример 5. Исследовать на непрерывность функцию .

Решение. Область определения: . Так как функция задана одной формулой, то она непрерывна на всей числовой прямой, за исключением, быть может, числа 0. Исследуем отдельно точку . Для начала вспомним, как определяется модуль числа: . Теперь вычислим односторонние пределы: { приближается к 0 со стороны отрицательных чисел, поэтому } , поэтому . С другой стороны, { приближается к 0 со стороны положительных чисел, поэтому } , поэтому . Итак, , а . По приведенной выше классификации точек разрыва точка есть точка разрыва 1-го рода (скачок). Величина скачка .

Пример 6. Исследовать на непрерывность функцию .

Решение. Область определения . Так как функция задана одной формулой, то она непрерывна на всей числовой прямой, за исключением, быть может, числа 0. Исследуем отдельно точку . Для этого вспомним не раз уже вычисленные выше следующие односторонние пределы: , . Тогда , . Таким образом, один (правый) из односторонних пределов оказался бесконечным. Этого уже достаточно, чтобы по принятой выше классификации объявить точку точкой разрыва 2-го рода.

Пример 7. Исследовать на непрерывность функцию .

Решение. Начало решения точно такое же. Область определения . Так как функция задана одной формулой, то она непрерывна на всей числовой прямой, за исключением, быть может, числа 0. Исследуем отдельно точку . Теперь воспользуемся вычисленными в предыдущем примере пределами: и . Тогда предел слева . Запишем предел справа: ={для избавления от неопределенности разделим числитель и знаменатель на }= . Итак, односторонние пределы , а . По классификации точек разрыва есть точка разрыва 1-го рода (скачок). Величина скачка .

Пример 8. При каком значении параметра функция непрерывна на всей числовой прямой.

Решение. При любом значении параметра функция определена на всей числовой прямой и задается двумя формулами на разных интервалах по : и . Поэтому при любом значении параметра функция непрерывна на всей числовой прямой, за исключением, быть может, точки (точка стыка двух формул). Осталось найти такое значение , при котором функция окажется непрерывной и в этой точке, что обеспечит непрерывность соответствующей функции на всей числовой прямой. Односторонние пределы в точке : , . Значение функции в самой точке : .

Для непрерывности в данной точке должны выполняться условия: , то есть . Очевидно, что это выполнено только при . Итак, только при заданная функция непрерывна на всей числовой прямой.