Оглавление

Раздел IV. Введение в математический анализ 4

Функция 4

Графики основных элементарных функций 8

Предел функции 12

Раскрытие неопределенностей в пределах 19

Замечательные пределы 23

Бесконечно малые и бесконечно большие функции 26

Односторонние пределы 29

Непрерывные функции 31

Свойства функций, непрерывных в точке 33

Свойства функций, непрерывных на отрезке 36

Точки разрыва функции 39

Классификация точек разрыва функции 40

Раздел V. Дифференциальное исчисление функции одного переменного 46

Производная функции 46

Механический, экономический и геометрический смысл производной 49

Правила нахождения производных. Таблицы производных 51

Уравнение касательной 56

Производные высших порядков 60

Дифференциал функции 61

Правило Лопиталя вычисления пределов 64

Раздел VI. Исследование функций с помощью производных 69

Монотонные функции 70

Экстремумы функции 73

Наибольшее и наименьшее значение функции, непрерывной на отрезке 84

Направление выпуклости графика функции и точки перегиба 88

Асимптоты графика функции 95

Общая схема исследования функции и построения графика 106

Раздел IV. Введение в математический анализ

Любая научная дисциплина имеет свой объект изучения, который называется предметом этой дисциплины. Предметом математического анализа являются функции.

Функция

Н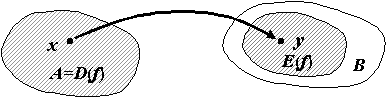 апомним определение функции. Пусть даны 2 множества произвольной структуры А и В. Будем говорить, что на множестве А задана функция, если имеется правило, по которому каждому элементу множества А поставлен в соответствие некоторый (один) элемент множества В. Символически это записывается в виде , где обозначает произвольный элемент множества А, а обозначает тот элемент множества В, который ставится в соответствие элементу . При этом говорят, что переменная является функцией переменной , а называется образом элемента при отображении (функции) (см. рисунок). Множество А называется областью определения функции (обозначается ), а множество элементов из В, в которые переводятся элементы из области определения (т.е. множество образов), называется областью значений функции (обозначается ). Множества А и В могут быть любой природы.

Пример 1. Рассмотрим множество А студентов, сидящих в данный момент в аудитории, и множество В всех стульев в данной аудитории. Каждому такому студенту поставим в соответствие тот стул, на котором он сидит (это и есть то правило, наличие которого содержится в определении функции). Тогда каждому студенту (т.е. элементу множества А) соответствует единственный (считаем, что никто не сидит на двух стульях) стул (т.е. элемент множества В). Тем самым задана функция, областью определения которой является множество А сидящих в аудитории студентов, а областью значений является некоторая часть стульев (или все стулья, если свободных не осталось) в данной аудитории.

Математический анализ изучает, в основном, числовые функции, когда область определения и область значений есть множества действительных чисел. Функция f при этом чаще всего задается некоторой математической формулой, поскольку именно с помощью формул удобно задавать правило, по которому одна числовая переменная зависит от другой. В этом случае функция символически записывается в виде , а обозначает соответствующую формулу.

Пример 2. Пусть функция задана формулой . Тогда для данного случая . Эта формула является компактной записью следующего правила, задающего функцию: для нахождения образа для некоторого заданного числа нужно произвести следующие действия: а) прибавить к нему 2; б) из полученного результата извлечь квадратный корень; в) к полученному прибавить 1; г) вычесть из заданного числа единицу; д) разделить результат пункта в) на результат пункта г). Областью определения является то множество чисел, для которых эта последовательность действий может быть осуществлена. Ограничения на действия с числами имеют только операции, перечисленные в пунктах б) и д), поскольку нельзя извлекать квадратный корень из отрицательных чисел и нельзя делить на 0. Поэтому задающее функцию правило применимо только для таких чисел , которые одновременно удовлетворяют двум условиям: или . Таким образом, область определения данной функции составляют все числа, которые больше либо равны числу (− 2), кроме числа 1: .

В случае числовой функции можно ввести понятие графика функции, который является ее геометрическим изображением и (как будет показано дальше) очень полезен для изучения характера зависимости одной переменной от другой. Графиком функции называется линия на координатной плоскости хОу, состоящая из точек, координаты которых удовлетворяют соотношению , которым задается функция. График функции можно строить, например, поточечно, задавая некоторый набор числовых значений переменной , вычисляя затем соответствующие значения функции и строя точки с полученными координатами. Затем эти точки соединяют плавной линией, что дает эскиз графика функции. Однако этот метод при своей трудоемкости (требуется построить как можно больше точек) дает лишь грубое представление о графике, если функция не слишком проста.

График функции обладает важным свойством, позволяющим определять значения функции «геометрически», не подставляя соответствующие значения независимой переменной х в формулу, а непосредственно из графика. Соответствующее правило легко следует из самого определения графика функции. А именно, если имеется график функции , то для получения значения этой функции при значении аргумента нужно (см. рисунок): а) найти точку на оси х, соответствующую числу . б) найти точку пересечения перпендикуляра к оси х в точке с графиком функции. в) опустить перпендикуляр из этой тоски на ось у. г) найти число соответствующей основанию этого перпендикуляра.

Тогда число и будет являться значением данной функции при (то значение, которое получилось бы, если подставить в формулу , вместо и посчитать). Этот факт записывается в виде: .

Напомним некоторые свойства числовых функций и отражение этих свойств на их графиках. Функция называется чётной (нечётной) , если выполнены следующие два условия: а) область определения функции представляет собой множество на числовой оси х, которое является симметричным относительно точки 0 (это означает, что если , то и ); б) для всех выполнено: (для нечетной функции : ). Свойство четности или нечетности функции следующим образом отражается на форме ее графика. График четной функции симметричен относительно оси у. Поэтому график такой функции можно строить только справа от оси у (т.е. только для ), а затем отразить полученную кривую относительно оси у. График нечетной функции симметричен относительно точки, которая является началом координат. График такой функции можно тоже строить только справа от оси у (т.е. только для ), а затем добавить симметричное отражение полученной кривой относительно начала координат. Если функция не является ни четной, ни нечетной, то она называется функцией общего положения.

Функция называется периодической, если существует такое число (оно называется периодом функции), для которого выполняются 2 условия: а) если , то и ; б) для всех выполнено: . Среди проходимых в школе функций периодическими были только тригонометрические функции (см. ниже). График периодической функции повторяет себя при сдвиге на величину периода вправо и влево вдоль оси х. Поэтому график периодической функции достаточно построить только над любым отрезком оси х длины , а затем периодически повторить его вправо и влево вдоль оси х. Напомним, как выглядят графики основных элементарных функций.