
- •"Теорія ймовірностей та математична статистика"
- •6.050102 – «Комп’ютерна інженерія»
- •Практичне заняття
- •1 Короткі теоретичні відомості
- •1.1 Розподіли статистик непараметричних критеріїв згоди при простих гіпотезах [3]
- •1.1.1 Критерій Колмогорова
- •1.1.2 Критерій Смірнова
- •1.1.3 Критерії
- •Постановка задачі
- •Варіанти завдань
- •Контрольні питання
- •Список літератури
- •Практична робота
- •«Теорія ймовірностей та математична статистика»
- •39600, М. Кременчук, вул. Першотравнева, 20
Постановка задачі
Випадкова
величина
![]() має розподіл
має розподіл
![]() ,
вектор параметрів
,
вектор параметрів
![]() якого відомий. Згенерувати згідно з
варіантом вибірку випадкової величини
:
якого відомий. Згенерувати згідно з
варіантом вибірку випадкової величини
:
![]() спочатку об’єму
спочатку об’єму
![]() ,
що має розподіл
,
обчислити
оцінку вектора параметрів розподілу
,
що має розподіл
,
обчислити
оцінку вектора параметрів розподілу
![]() .
Висунути статистичну гіпотезу щодо
закону розподілу випадкової величини,
виходячи з конкретного варіанта і
перевірити її з надійністю
.
Висунути статистичну гіпотезу щодо
закону розподілу випадкової величини,
виходячи з конкретного варіанта і
перевірити її з надійністю
![]() за допомогою критеріїв
за допомогою критеріїв
![]() Пірсона, Романовського, Колмогорова-Смірнова
(для неперервних розподілів) та
–
Мізеса. Повторити дослідження для
Пірсона, Романовського, Колмогорова-Смірнова
(для неперервних розподілів) та
–
Мізеса. Повторити дослідження для
![]() .
Порівняти результати, зробити висновки.
.
Порівняти результати, зробити висновки.
У теоретичній частині необхідно:
Навести схеми застосування вищезгаданих статистичних критеріїв.
У частині проведення модельного експерименту необхідно:
Згенерувати вибірку обсягу
 .
Знайти статистичний розподіл у вигляді
статистичної таблиці (для дискретних
випадкових величин) чи у вигляді
інтервальної статистичної таблиці
(для неперервної випадкових величини).
.
Знайти статистичний розподіл у вигляді
статистичної таблиці (для дискретних
випадкових величин) чи у вигляді
інтервальної статистичної таблиці
(для неперервної випадкових величини).Отримати точкові оцінки параметрів гіпотетичного розподілу.
Знайти оцінки параметра форми розподілу
 ,
контрексцесу
,
контрексцесу
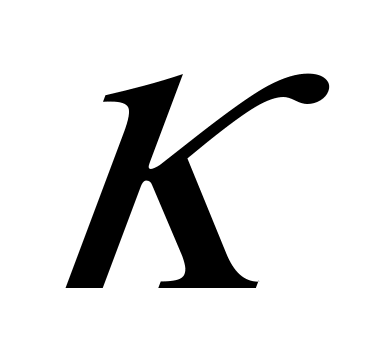 та ентропійного відношення
та ентропійного відношення
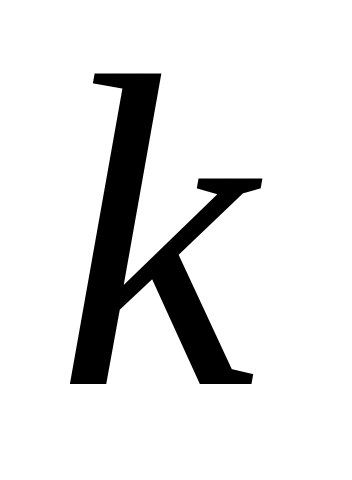 .
.Побудувати графіки (в пакеті MathCAD):
а)
емпіричної (сходинкової) та теоретичної
![]() функцій розподілу (на одному графіку);
функцій розподілу (на одному графіку);
б)
теоретичної щільності
![]() розподілу та гістограму (на одному
графіку) для
неперервних випадкових величин,
або багатокутник розподілу
розподілу та гістограму (на одному
графіку) для
неперервних випадкових величин,
або багатокутник розподілу
![]() для
дискретних випадкових величин
та полігон (на одному графіку).
для
дискретних випадкових величин
та полігон (на одному графіку).
4. Розрахувати вибіркові значення критеріїв Колмогорова-Смірнова, Пірсона, Романовського та .
5. Перевірити нульову гіпотезу, зробити висновки.
6.
Повторити п. 1-5 для
![]() .
Порівняти результати, зробити висновки.
.
Порівняти результати, зробити висновки.
7. Виконати робоче завдання в середовищі Statgraphics. Порівняти результати з тими, що отримані в середовищі MathCAD.
Скласти електронний звіт у форматі Microsoft Word згідно з вимогами ЄСКД. Структура звіту:
Титульна сторінка.
Постановка задачі.
Короткі теоретичні відомості стосовно досліджуваного розподілу та методів розрахунків.
Детальна схема виконання лабораторної роботи з необхідними екранними формами і поясненнями згідно з робочим завданням, результатами аналізу.
Висновки.
Перелік посилань.
До звіту додати:
Файл Microsoft Excel (за необхідності) з матрицею згенерованих даних.
Файл у форматі MathCAD 11 зі статистичними проектами.
Варіанти завдань
Рівномірний розподіл з параметрами
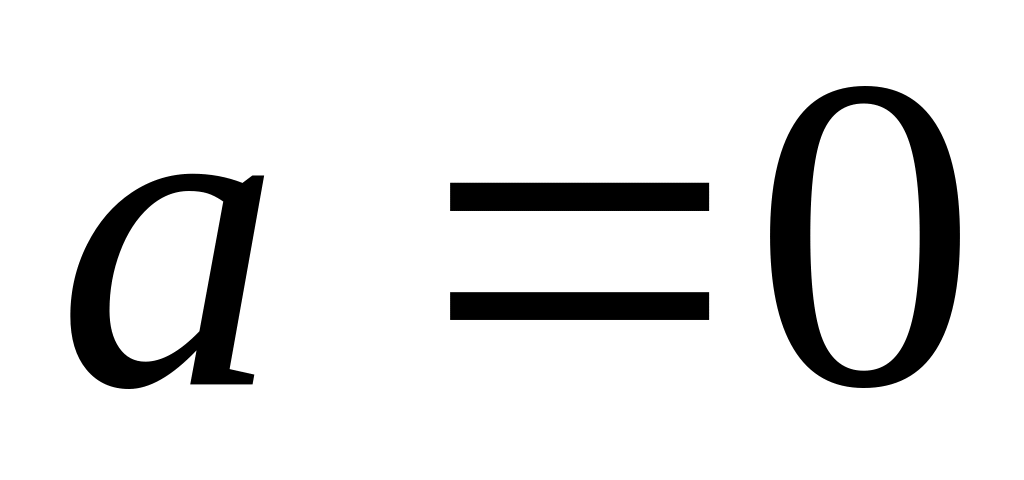 ,
,
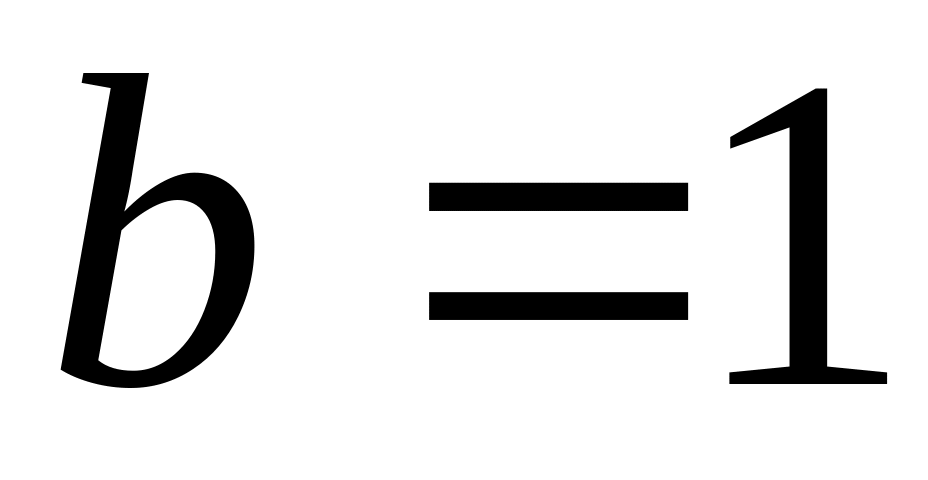 .
.Нормальний розподіл з параметрами ,
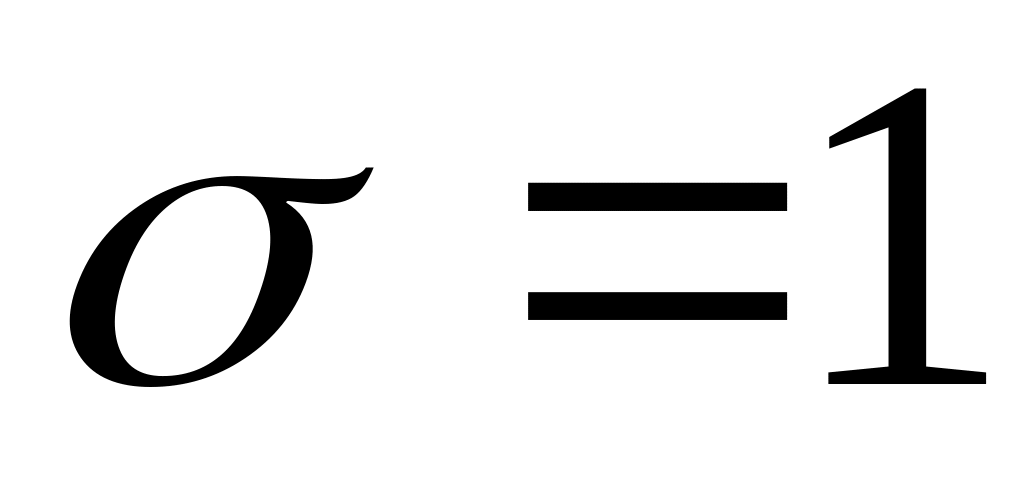 .
.Рівномірний розподіл з параметрами
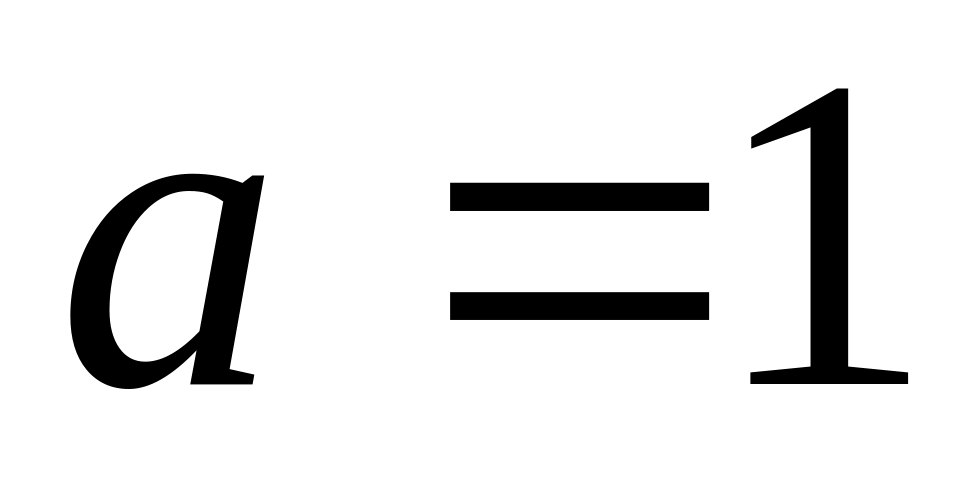 ,
,
 .
.Нормальний розподіл з параметрами ,
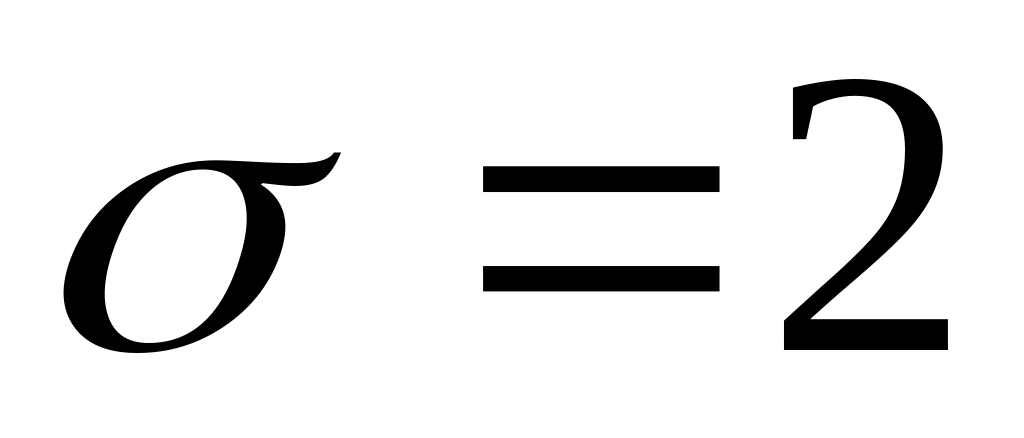 .
.Рівномірний розподіл з параметрами
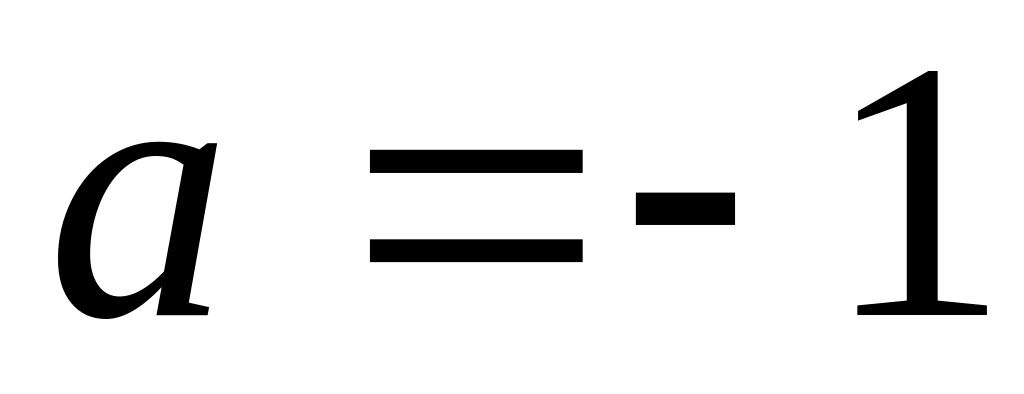 ,
.
,
.Нормальний розподіл з параметрами ,

Експоненціальний розподіл з параметром
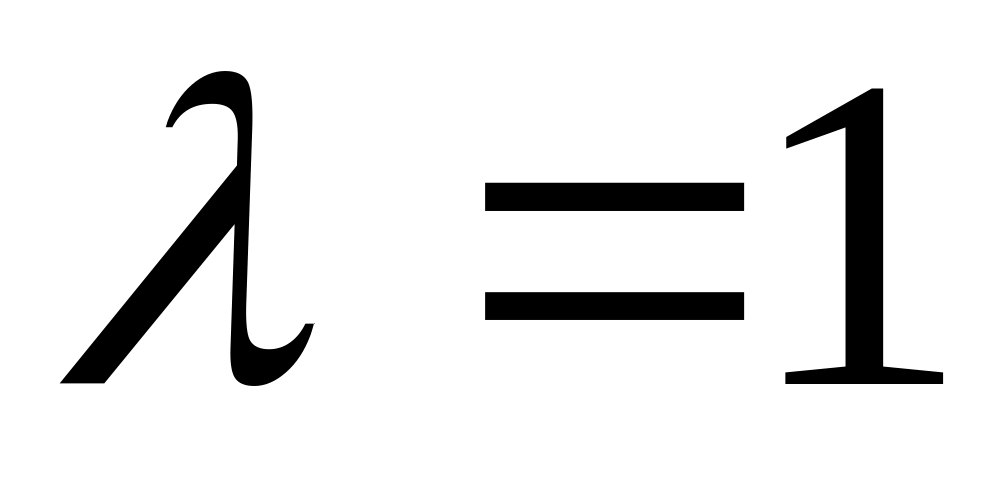
Розподіл Пуассона з параметром
Експоненціальний розподіл з параметром
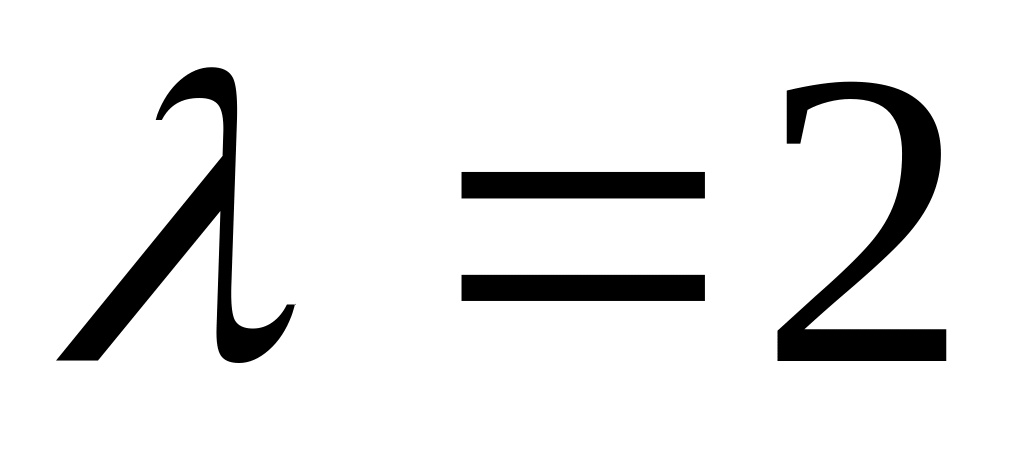
Розподіл Пуассона з параметром
Біноміальний розподіл з параметрами р=0.5, n=100
Біноміальний розподіл з параметрами р=0.7, n=50
Розподіл Стьюдента з
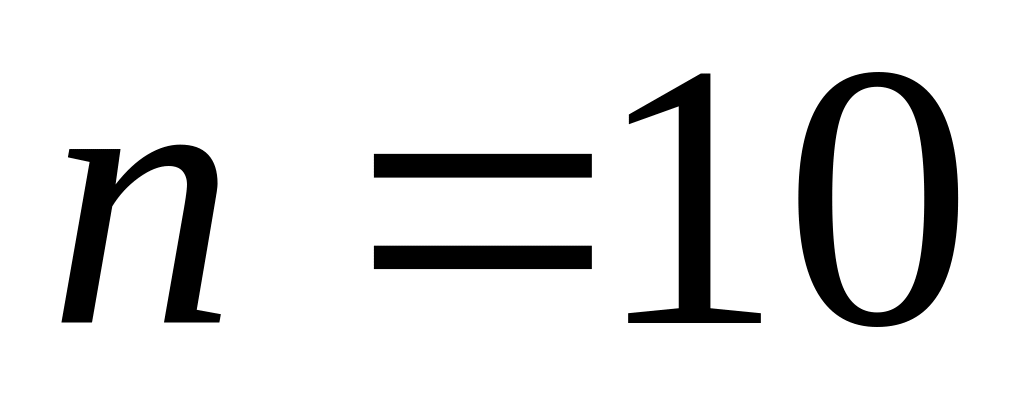 степенями вільності
степенями вільностіРозподіл Стьюдента з
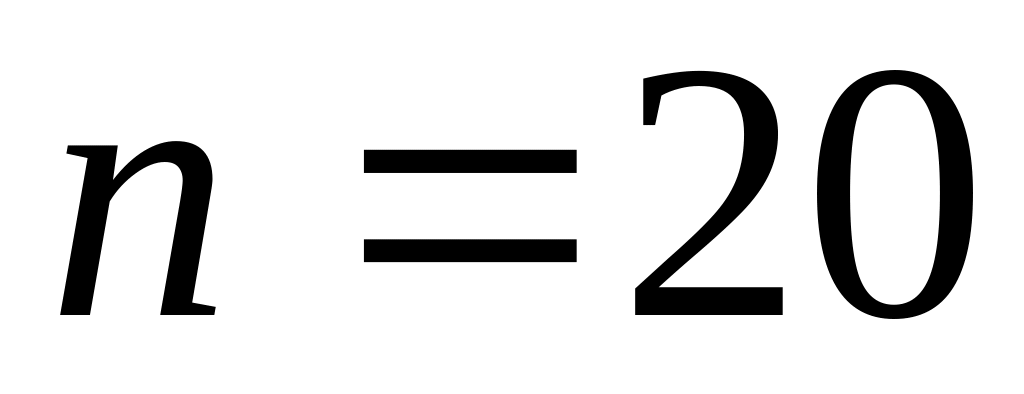 степенями вільності
степенями вільностіРозподіл
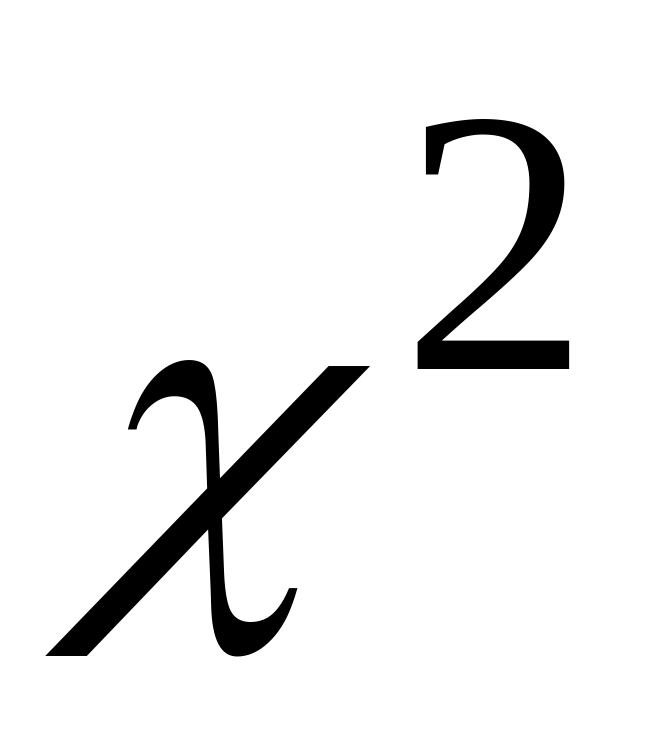 з
з
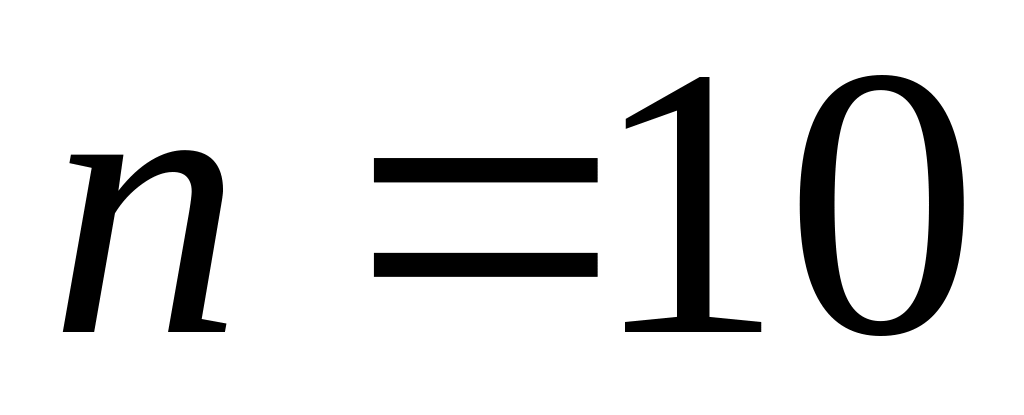 степенями вільності
степенями вільностіРозподіл з
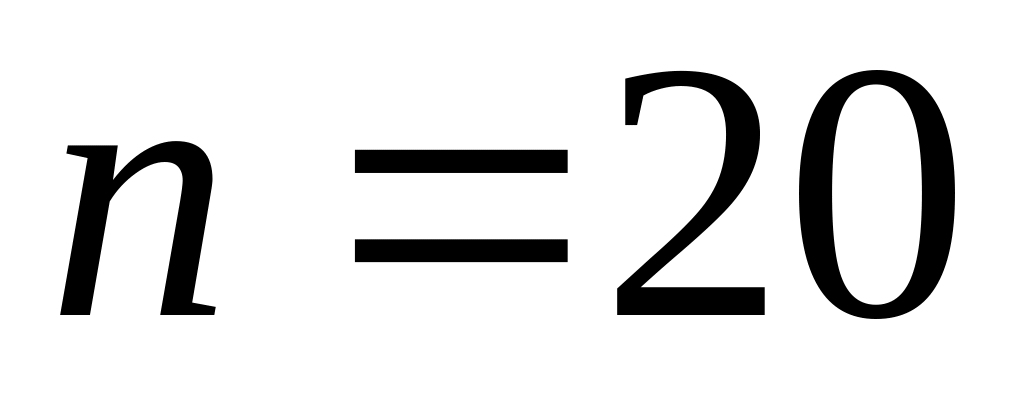 степенями вільності
степенями вільностіЛогарифмічний нормальний розподіл з параметрами і .
![]() ,
,
![]()
Логарифмічний нормальний розподіл з параметрами і . Див. вар. 17
Розподіл Фішера з параметрами і
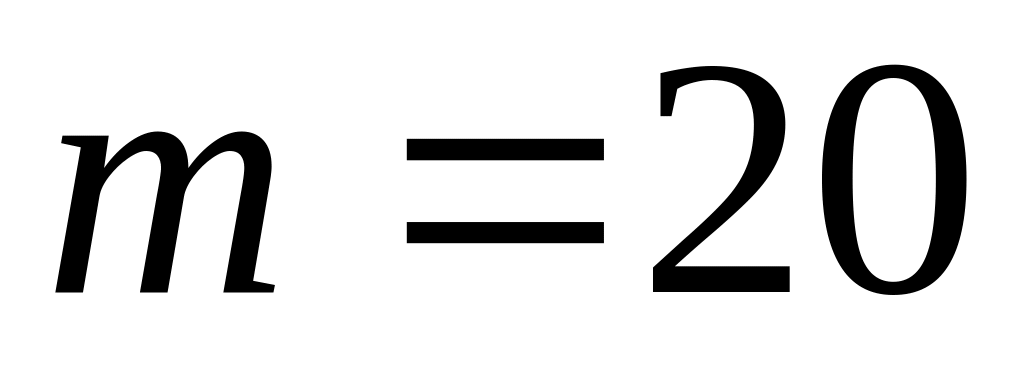
Розподіл Фішера з параметрами і
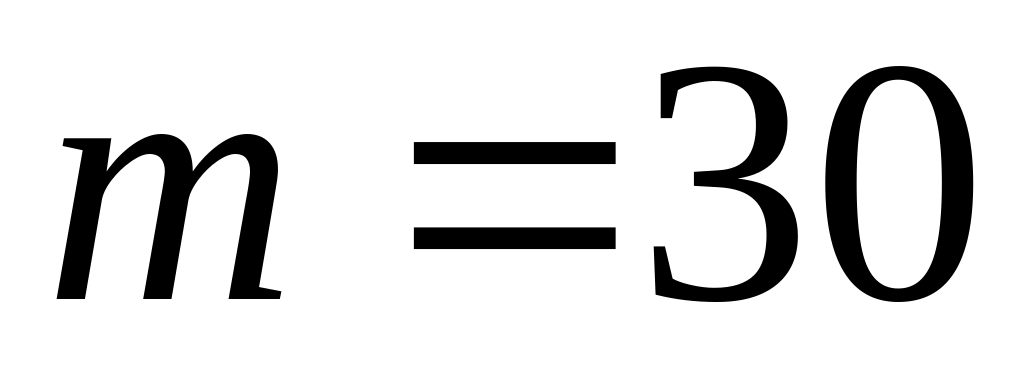
Нормальний усічений розподіл [5] з параметрами ,
 ,
,
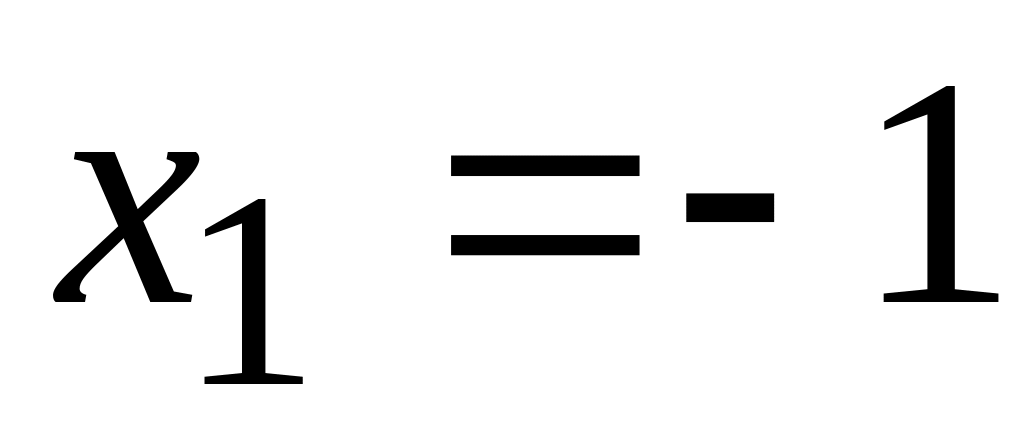 ,
,
 .
.
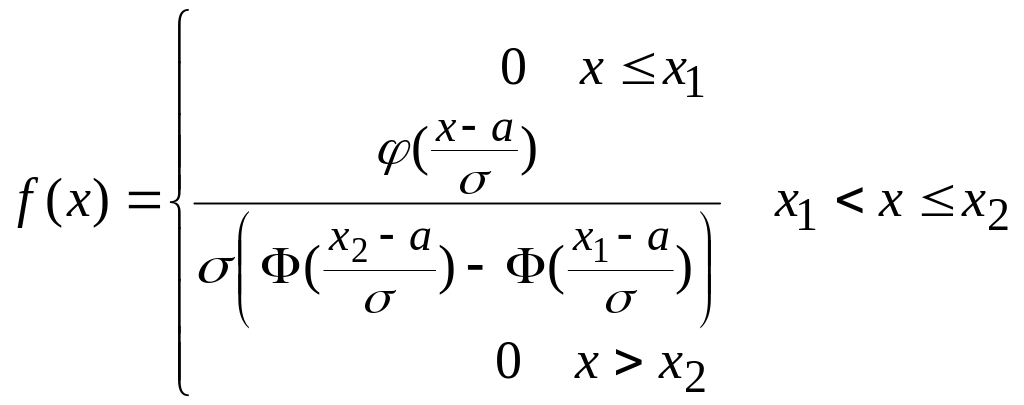 ,
де
,
де
![]() –
функція Лапласа,
–
функція Лапласа,
![]() –
інтегральна функція Лапласа.
–
інтегральна функція Лапласа.
 ,
(*)
,
(*)
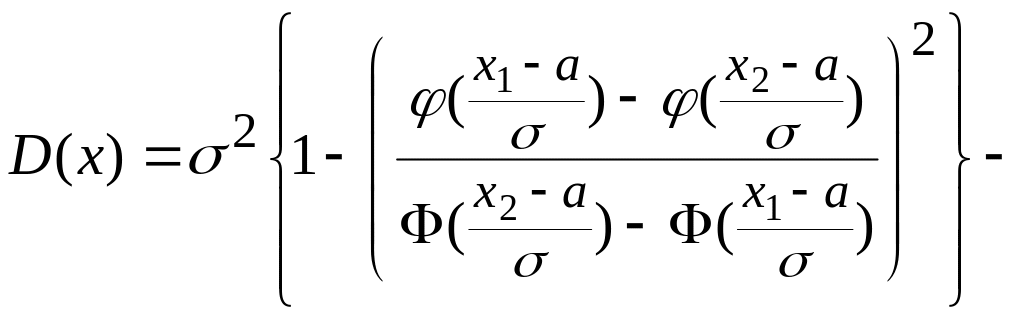
 .
(**)
.
(**)
Розподіл Коші з параметрами
 ,
,

![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
де
![]() –
ціла частина числа;
–
ціла частина числа;
![]() ,
–
вибірковий квантиль до рівнює 0.75, тобто
,
–
вибірковий квантиль до рівнює 0.75, тобто
![]() -й
член варіаційного ряду, побудованого
за даною вибіркою;
-й
член варіаційного ряду, побудованого
за даною вибіркою;
![]() –
медіана.
–
медіана.
Трапецієдальний розподіл [1,2] з параметрами
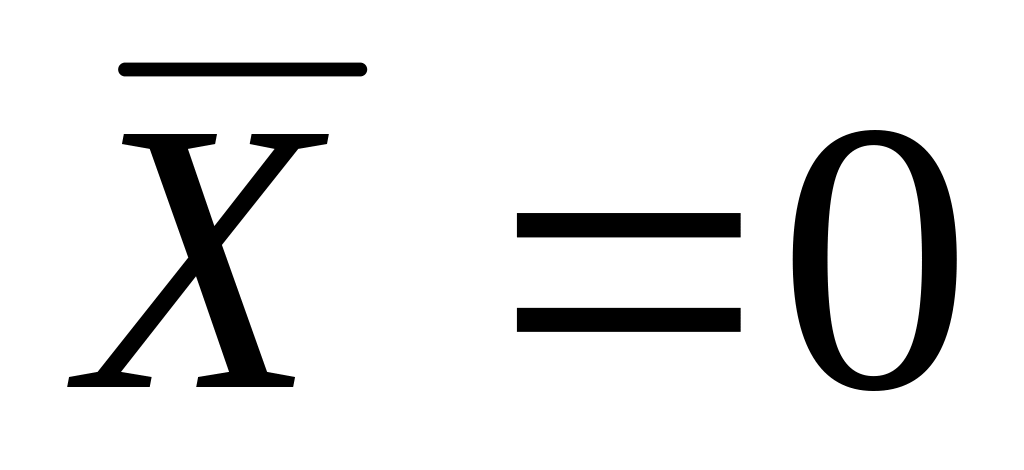 ,
,
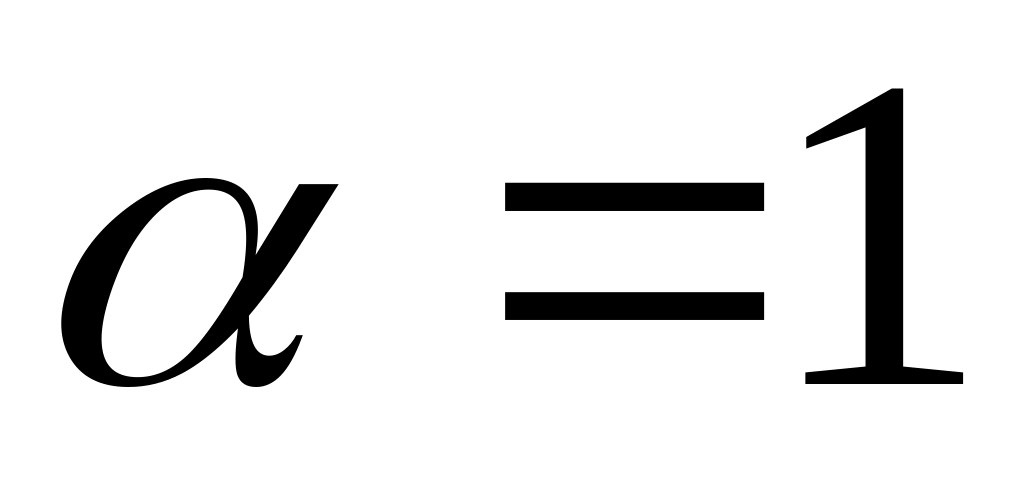 ,
,
 .
.
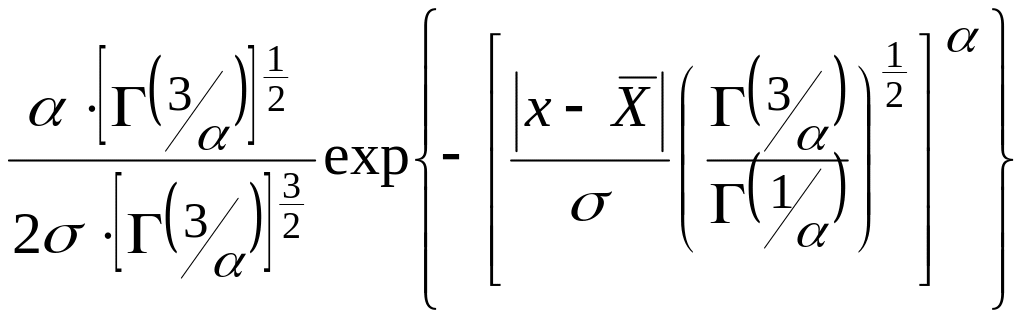 ,
,
![]()
Розподіл Сімпсона (трикутний) симетричний з параметром .
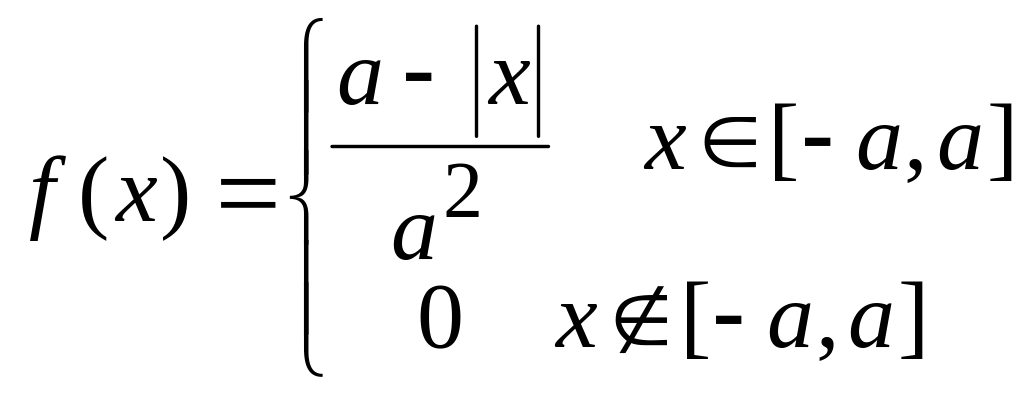
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
