Практичне заняття

Тема. перевірка статистичних гіпотез. установлення виду математичної моделі розподілу випадкової величини

Мета: закріплення на практиці таких понять, як статистична гіпотеза, параметричні та непараметричні статистичні критерії; набуття навичок у використанні можливостей пакетів MathCAD та Statgraphics для обчислення значень статистичних критеріїв та перевірки за допомогою їх статичних гіпотез щодо закону розподілу випадкової величини, зокрема з використанням стандартних функцій для розрахунку квантилів.

1 Короткі теоретичні відомості

Характеристики, що дозволяють виконати топографічну класифікацію розподілу згідно з [1, 2]:

- Коефіцієнт форми знаходиться як

, (1)

де – оцінка ексцесу.

- Оцінка ентропійного коефіцієнта:

, (2)

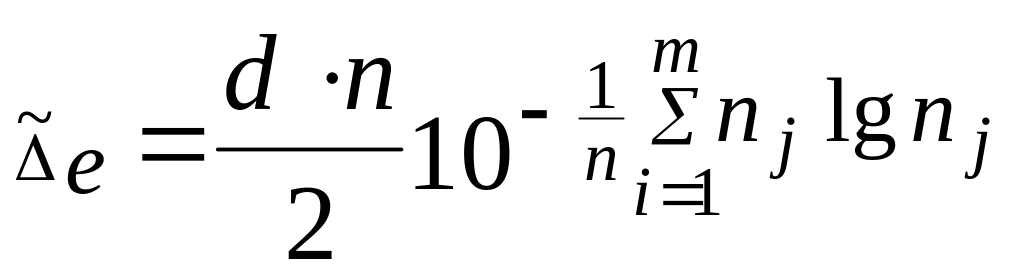де – вибіркове виправлене СКВ; – вибіркове ентропійне значення похибки; d – ширина інтервалу вибіркового розподілу; m – число інтервалів; n – об’єм вибірки; – частоти;

- Оцінка контрексцеса

, (3)

де – вибірковий центральний момент 4-го порядку; – середнє арифметичне.

1.1 Розподіли статистик непараметричних критеріїв згоди при простих гіпотезах [3]

1.1.1 Критерій Колмогорова

У разі простих гіпотез граничні розподіли статистик даних критеріїв згоди Колмогорова, Смірнова, і Мізеса відомі та не залежать від виду спостережуваного закону розподілу і, зокрема, від його параметрів. Говорять, що ці критерії є “вільними від розподілу”. Це достоїнство зумовлює широке використання даних критеріїв на практиці.

Розподіл статистики

, (4)

де – емпірична функція розподілу, – теоретична функція розподілу, – об'єм вибірки, було отримано Колмогоровим. При розподіл статистики збігається рівномірно до розподілу Колмогорова

. (5)

Найчастіше в критерії Колмогорова (Колмогорова-Смірнова) використовується статистика виду

, (6)

де

, (7)

, (8)

, (9)

де - об'єм вибірки, – впорядковані за збільшенням вибіркові значення, – функція закону розподілу, згода з яким перевіряється. Розподіл величини при простій гіпотезі в межі підкоряється закону Колмогорова .

Якщо для обчисленого щодо вибірки значення статистики виконується нерівність

, то немає підстав для відхилення гіпотези .

1.1.2 Критерій Смірнова

У критерії Смірнова використовується статистика

, (10)

або статистика

, (11)

значення яких обчислюються за еквівалентними співвідношеннями (8),(9).

Реально в критерії звичайно використовується статистика [3]

, (12)

яка при простій гіпотезі в межі підкоряється розподілу з числом степенів вільності, що дорівнює 2.

Гіпотеза не відкидається, якщо для обчисленого щодо вибірки значення статистики :

.

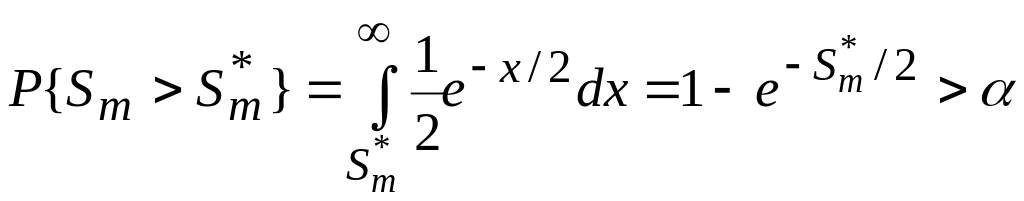1.1.3 Критерії

У критеріях типу відстань між гіпотетичним та істинним розподілами розглядається в квадратичній метриці.

Гіпотеза , що перевіряється, має вигляд

(13)

при альтернативній гіпотезі

, (14)

де – оператор математичного сподівання, – задана на відрізку ненегативна функція, щодо якої передбачається, що , , є інтеґровними на відрізку . Статистика критерію виражається співвідношенням

, (15)

де

, .

При виборі для критерію Мізеса одержують статистику вигляду (статистику Крамера-Мізеса-Смірнова)

, (16)

яка при простій гіпотезі підкоряється розподілу, що має вигляд [3]

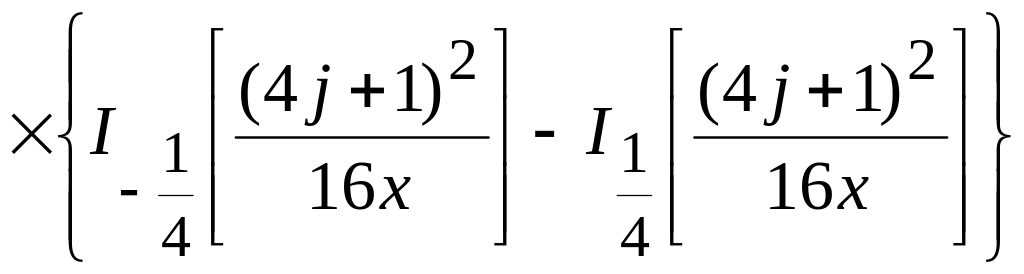, (17)

де – модифіковані функції Бесселя,

. (18)

При виборі для критерію Мізеса статистика набуває вигляду (статистика Андерсона-Дарлінга)

. (19)

У межі ця статистика підлягає розподілу, що має вигляд

. (20)

Гіпотези про згоду не відкидаються, якщо виконуються нерівності

і .

Методичні рекомендації. Перш ніж приступати до виконання індивідуального завдання, необхідно опрацювати матеріал лекцій № 4 - 5 розділу «Математична статистика» курсу «Теорія ймовірностей та математична статистика», електронна версія якої міститься на веб-сервері кафедри. Далі отримати номер варіанта завдання у викладача. Після цього приступити до опрацювання пункту методичних вказівок «Постановка задачі» та вивчення відповідного прикладу виконання завдання в середовищі MathCAD (додаток А), електронна версія якого також міститься на веб-сервері кафедри у розділі «Методичні вказівки до самостійної роботи». Наступним етапом є виконання індивідуального завдання в середовищі MathCAD, а потім у середовищі Statgraphics. Після цього приступити до оформлення звіту.