14.5. Уравнения Максвелла в комплексной форме записи
Уравнения (14.1) и (14.4) записаны для мгновенных значений. Если H и E изменяются во времени синусоидально, то можно воспользоваться символическим методом и записать, эти уравнения (14.1) и (14.4) в иной форме. Пусть
Н = Нm sin (t + н) и Е = Еm sin (t + Е).
Можно записать Н
= Im Hmejt
(Im — мнимая часть)
или, условно, Н
ejt,
где комплексная амплитуда
= Нmejн.
В свою очередь Е
ejt
( - значок соответствия).
Так как напряженности
Е и Н, кроме того, что они меняются
во времени по синусоидальному закону,
являются функциями векторными, т. е.
определенным образом ориентированными
в пространстве векторами, то над ними
ставят стрелку и точку:
и
.
Стрелка означает, что речь идет о векторе
в пространстве, точка — о том, что
проекции этого вектора на любую из
координатных осей во времени изменяются
синусоидально. Тогда
можно заменить на
ejt:
на
,
и
на
,
(еjt как постоянную величину, не зависящую от координат, можно вынести за знак ротора). При этом первое уравнение Максвелла запишем так:
.
После сокращения на еjt получим
.
(14.6)
Аналогично, второе уравнение Максвелла в комплексной форме
.
(14.7)
14.6. Теорема Пойнтинга для мгновенных значений
Кроме уравнений
Максвелла, большое значение в теории
электромагнитного поля имеет теорема
Пойнтинга, которая описывает энергетические
соотношения в поле. Известно, что энергия
электрического поля в единице объема
равна
,
а энергия магнитного поля
в
единице объема равна
.
Энергия в объеме dV
равна (
)dV.
Для того чтобы образовать выражение, в которое вошла бы полная энергия в объеме dV, умножим (14.1) на EdV, a (14.4) на HdV. Получим:
;
(14.8)
.
(14.9)
Из (14.8) вычтем (14.9). Получим
.
(14.10)
Так как div [EH] = HrotE —ErotH, то левая часть (14.10) есть - div[EH]dV. Следовательно,
.
Д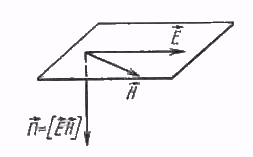
ля
сокращения записи обозначим векторное
произведение E на Н
через П. т. е. примем, что П = [EH];
П —это вектор, называемый (
)
вектором Пойнтинга; размерность его
равна произведению размерностей Е и Н:
[П]=[Е][Н]=
=ВА/м2.
Рис. 14.1. Вектор Пойнтинга направлен перпендикулярно плоскости, в которой расположены векторы Е и Н.
Таким образом, вектор Пойнтинга имеет размерность мощности (или энергии в единицу времени), отнесенной к единице поверхности, и направление его (рис. 14.1) совпадает с направлением движения острия правого винта, если головку последнего вращать по кратчайшему направлению от Е к Н. Следовательно,
.
(14.11)
Распространим (14.11) на некоторый объем конечных размеров. С этой целью проинтегрируем (14.11) по объему V:
.
(14.11')
Подобно тому, как
поверхностный интеграл по теореме
Стокса преобразовывается в линейный:
,
объемный интеграл в свою очередь может
быть преобразован в поверхностный. Это
преобразование осуществляют с помощью
теоремы Гаусса
.
Качественно поясним это преобразование.
Разобьем объем V (рис. 14.2) на отдельные
объемы V,
заменим div П на
, где S
— элемент поверхности объема V,
а знак означает
суммирование по всем поверхностям
объема V.
Тогда
.
Первый
знак суммы означает суммирование по
поверхностям малого объема, а второй —
по отдельным объемам. Сумма
может быть разбита на две суммы: на сумму
выражений
по всем поверхностям, отделяющим один
объем от соседнего (по «внутренним»
поверхностям), и на сумму
по всем «периферийным» поверхностям.
Первая сумма равна нулю, так как для
двух смежных объемов внешние нормали
к общей поверхности направлены встречно.
Рис. 14.3 поясняет это; mn
— общая грань двух объемов.
Рис.
14.2. Объём V разбит на отдельные объёмы
ΔV.
Р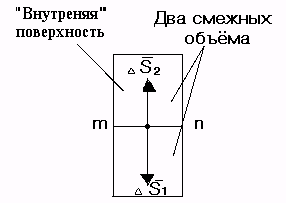
ис.
14.3.Два смежных объёма ΔV выделенных из
общего объёма
Для верхнего объема
нормаль к грани направлена вниз (S1),
для нижнего — вверх (S2);
вектор П, будучи умноженным на (S1
+ S2),
даст нуль. Сумма
по всем периферийным поверхностям и
представляет собой
.
Теорему Пойнтинга для мгновенных значений записывают следующим образом:
,
(14.12)
Левая часть (14.12) представляет собой поток вектора Пойнтинга (направленный внутрь объема) сквозь любую замкнутую поверхность S, ограничивающую некоторый объем V.
Поясним смысл знака «минус» в левой части формулы (14.12). Элемент поверхности dS в любой ее точке направлен в сторону внешней по отношению к рассматриваемому объему нормали. Вектор Пойнтинга П направлен внутрь этого объема. Поскольку угол между П и dS больше 90°, то скалярное произведение ПdS < 0, а —ПdS > 0. Таким образом, за счет знака «минус» левая часть формулы (14.12) — величина положительная.
В соответствии с
уравнением Джоуля— Ленца в дифференциальной
форме Е2
есть энергия, выделяющаяся в виде теплоты
в единице объема в единицу времени.
Поэтому
есть энергия, выделяющаяся в виде теплоты
в единицу времени в объеме V;
есть скорость изменения запаса
электромагнитной энергии в единице
объема.
Но скорость изменения электромагнитной энергии есть мощность. Следовательно, поток вектора Пойнтинга сквозь любую замкнутую поверхность, ограничивающую объем V, равен мощности, выделяющейся в объеме V в виде теплоты, и мощности, идущей на приращение энергии электромагнитного поля. Теорему Пойнтинга следует трактовать как уравнение энергетического баланса; левая часть (14.12) есть мощность или энергия в единицу времени, доставляемая в виде потока вектора Пойнтинга внутрь некоторого объема; правая часть (14.12) есть энергия, расходуемая в единицу времени внутри объема. Соотношение (14.12) было получено в предположении, что среда внутри объема V однородна и изотропна, а также в предположении, что отсутствует отраженная волна, и внутри объема нет источников электродвижущей силы.
Если поле не изменяется во времени, то
0 и
.
Обратим внимание также на то, что формула (14.12) учитывает возможность прохождения потока вектора П транзитом через объем V. Электромагнитная энергия от места ее генерирования передается к месту потребления по диэлектрику (провода же в линиях передачи выполняют двоякую роль: они являются каналами, по которым проходит ток, и организаторами структуры поля в диэлектрике).
П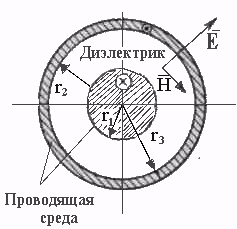
окажем
справедливость этого утверждения на
простейшем примере. Пусть энергия
постоянного тока передается по
коаксиальному кабелю (рис. 14.4). Радиус
жилы r1,
внутренний радиус оболочки r2.
Примем проводимость материала жилы и
оболочки настолько большой (теоретически
бесконечно большой), что напряженности
поля Е = /
в жиле и оболочке стремятся к нулю.
Пространство между жилой и оболочкой
заполнено диэлектриком. Убедимся, что
энергия, передаваемая приемнику в
единицу времени, равная UI,
действительно канализируется по
диэлектрику. С этой целью подсчитаем
поток вектора Пойнтинга через поперечное
сечение диэлектрика, в рассматриваемом
примере представляющее собой кольцо с
внутренним радиусом r1
и наружным r2.
Напряженность магнитного поля в
диэлектрике, по закону полного тока:
.
Рис. 14.4. Коаксиальный кабель.
Напряженность электрического поля в диэлектрике при постоянном токе определяется так же, как и в условиях электростатики:
,
где Q — полный заряд жилы на длине l; U — напряжение между жилой и оболочкой.
Следовательно, в некоторой точке диэлектрика, расположенной на расстоянии r от оси (r1 r r2),
,
(Е и H взаимно перпендикулярны; рис.14.4). Поток вектора Пойнтинга через кольцо с радиусами r1 и г2.
.
Таким образом, вся поступающая к приемнику энергия действительно передается по диэлектрику. По жиле и оболочке энергия к приемнику не передается. Более того, если учесть, что конечна и напряженность электрического поля в жиле и оболочке направлена по току и не равна нулю, то нетрудно убедиться в наличии потока вектора Пойнтинга через боковую поверхность провода внутрь провода, т. е. провода сами потребляют из диэлектрика энергию на покрытие тепловых потерь.