11.10. Свободные и связанные заряды. Поляризация вещества
Свободными зарядами называют заряды, которые под воздействием сил поля могут свободно перемещаться в веществе, их перемещение не ограничивается внутримолекулярными силами.
Под связанными зарядами принято понимать электрические заряды, входящие в состав вещества и удерживаемые в определенных положениях внутримолекулярными силами. Такие заряды «связаны» с данным веществом, неотделимы от него. Сумма положительных связанных зарядов равна сумме отрицательных связанных зарядов.
Если какое-либо диэлектрическое тело поместить в электрическое поле, то оно поляризуется.
Под поляризацией понимают упорядоченное изменение расположения связанных зарядов в теле, вызванное электрическим полем. Это изменение расположения проявляется в том, что отрицательные связанные заряды в теле переместятся в направлении более высокого потенциала, а положительные связанные заряды переместятся в сторону более низкого потенциала. Заряды сместятся настолько, что силы воздействия электрического поля на связанные заряды уравновесятся внутримолекулярными силами. В результате поляризации на поверхности вещества как бы обнажаются связанные заряды.
11.11. Вектор поляризации
Электрическим моментом двух равных по величине и противоположных по знаку зарядов, находящихся друг от друга на расстоянии l (диполя), называют произведение ql. Это векторная величина, направленная от заряда -q к заряду +q (рис. 11.6, а).
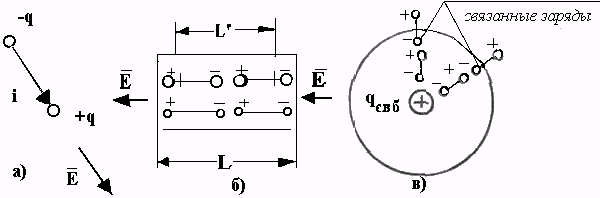
Рис. 11.6. К вопросу поляризации вещества: а) – электрический диполь, б) – электрический момент суммы диполей, в) – расположение связанных зарядов в диэлектрике.
В поляризованном веществе молекулы в электрическом отношении представляют собой диполи. Под действием внешнего электрического поля диполи стремятся ориентироваться в пространстве таким образом, чтобы электрический момент их был направлен параллельно вектору напряженности электрического поля. Практический интерес представляет электрический момент не одной молекулы, не одной пары зарядов, а суммы диполей, находящихся в единице объема вещества.
Электрический
момент суммы диполей, находящихся в
единице объема вещества, называют
вектором поляризации и обозначают
буквой
.
(11.12)
Для большинства диэлектриков Р пропорционален напряженности электрического поля Е. Коэффициент пропорциональности между ними обозначают обычно через k и называют электрической восприимчивостью
.
(11.13)
Все диэлектрики в отношении происходящих в них процессов при поляризации могут быть разбиты на 2 группы.
В первую группу входят диэлектрики, молекулы которых при отсутствии внешнего электрического поля электрически нейтральны, т.е. в них центры действия положительных и отрицательных зарядов совпадают. К числу таких диэлектриков относятся водород, азот, парафин, слюда и др.
Поляризация в диэлектриках первой группы состоит в том, что под действием внешнего электрического поля центр действия положительного заряда молекулы сместится по внешнему полю, а центр действия отрицательных зарядов сместится против поля. В результате молекула становится диполем. Это смещение зарядов молекулы пропорционально величине напряженности внешнего поля. Смещению противодействуют внутримолекулярные силы.
Во вторую группу диэлектриков входят диэлектрики, молекулы которых при отсутствии внешнего электрического поля представляют собой диполи. Другими словами, центры действия положительных и отрицательных зарядов этих молекул при отсутствии внешнего электрического поля не совпадают (полярные молекулы). В качестве диэлектрика с полярными молекулами может быть назван, например, хлористый водород.
Благодаря тепловому движению диполи располагаются хаотично, так что при отсутствии внешнего электрического поля их электрические поля взаимно нейтрализуются. Поляризация в диэлектриках второй группы состоит в том, что полярные молекулы стремятся повернуться таким образом, чтобы их электрический момент был направлен по внешнему электрическому полю.