§4. Дополнительные задачи

Размещения.

Задача №8. В некоторой газете 24 страниц. Необходимо на страницах этой газеты поместить 6 фотографий. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Для решения задачи необходимо найти по формуле (1) число размещений . Произведение в формуле для числа размещений можно найти с помощью обычного калькулятора. Воспользуемся возможностями MATLAB. В пакете MATLAB массив чисел x = {24, 23, 22, 21, 20, 19} можно записать компактно с помощью оператора двоеточие “:” в следующем виде x = 24:-1:19. Для решения задачи загрузим в командное окно MATLAB следующую функцию¹:

>> prod(24:-1:19)

После нажатия Enter в командном окне MATLAB появится ответ: 96909120 способов.

Задача №9. Сколько можно записать четырехзначных чисел, используя без повторения все десять цифр?

Для решения данной задачи отметим, что число 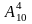четырехзначных цифр без повторений включает числа начинающиеся с 0, например, 0123, 0987 и пр. Таких цифр всего будет . Вычтем их из всего количества четырехзначных цифр, т.е. найдем разность . Для подсчета искомой разности загрузим в MATLAB следующее выражение:

>>prod(10:-1:7) - prod(9:-1:7)

После нажатия Enter в командном окне MATLAB появится ответ: 4536 способов.

Перестановки.

Задача №10. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Ответ к данной задаче может быть получен с помощью следующей формулы: P₆P₄ = 6!4! Для подсчета числа вариантов загрузим в MATLAB произведение:

>>factorial(6)*factorial(4)

После нажатия Enter в командном окне MATLAB появится ответ: 17280 способов.

Сочетания.

Задача №11. Необходимо выбрать в подарок 5 из 12 имеющихся различных книг. Сколькими способами это можно сделать?

Поскольку искомое количество вариантов определяется числом сочетаний, , постольку найдем их число с помощь средств MATLAB:

>>nchoosek(12,5)

После нажатия Enter в командном окне MATLAB появится ответ: 792 способа.

Задача №12. Имеется 10 белых и 5 черных шаров. Сколькими способами можно выбрать 7 шаров, чтобы среди них были 3 черных?

Искомое количество вариантов подсчитывается по формуле . Для получения численного результата загрузим в командное окно MATLAB выражение:

>>nchoosek(10,4)*nchoosek(5,3)

После нажатия Enter в командном окне MATLAB появится ответ: 2100 способов.

Задача №13. Сколькими способами можно группу из 12 человек разбить на две подгруппы, в одной из которых должно быть не более пяти, а во второй — не более девяти человек?

Искомое количество вариантов подсчитывается по формуле . Для получения численного результата загрузим в командное окно MATLAB выражение:

>>nchoosek(12,3)+nchoosek(12,4)+nchoosek(12,5)

После нажатия Enter в командном окне MATLAB появится ответ: 1507 способов.

Задача №14. Доказать равенство Паскаля .

Задача №15. Доказать равенство .

1 Функция prod(x) находит произведение элементов массива x, более подробно об этой функции в пакете MATLAB после запроса >>help prod

— 12 —