Расчет валковых машин

Вальцы являются основными машинами, применяемыми в течение многих лет для предварительной обработки исходных материалов при производстве кирпича и керамических труб, однако до настоящего времени не существует точной и надежной законченной инженерной методики расчета распорных усилий и напряжений сдвига в рабочем канале вальцев для обработки пластичных глин и, следовательно, не могут быть теоретически определены и рекомендованы обоснованные рациональные режимы их работы. На кафедре механического оборудования предпринята попытка создания методики расчета глинообрабатывающих вальцев с использованием известных гидродинамических методов расчета валковых машин для переработки полимерных материалов.

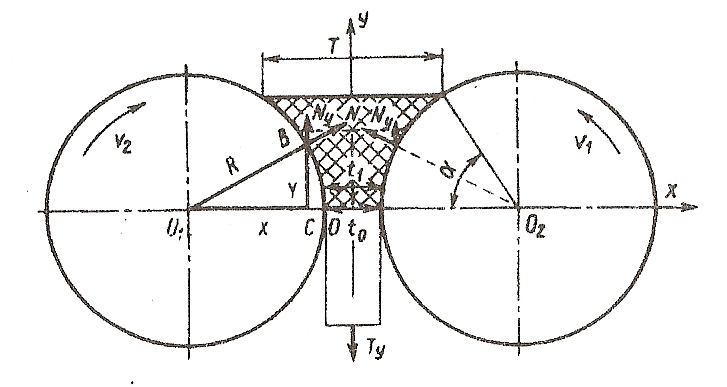
Рис.40 Расчетная схема вальцев

Движение глиняной массы в рабочем канале, образованном поверхностями валков, происходит в направлении, указанном на рис.40. Вследствие этого в исходных уравнениях можно отбросить члены, содержащие и производные по z. Ввиду малой высоты канала, пренебрегая действием массовых сил (F = 0) и принимая процесс движения керамической массы в канале, образованном движущимися стенками валков, установившимся , получим систему у равнений Навье-Стокса, описывающую плоскопараллельное движение вязкого материала:

, (278)

(279)

Двойное интегрирование первого уравнения этой системы к зависимости

. (280)

где и ­­- ­постоянные интегрирования.

Постоянные интегрирования и ­­ для случая, когда валки имеют разную окружную скорость, найдем, воспользовавшись граничными условиями:

при и fv при , (281)

где f - отношение окружных скоростей валков; v- окружная скорость валка.

После подстановки найденных значений и ­­ в формулу (280) и упрощающих преобразований получим скорость частиц потока материала

. (282)

Производную dp/dy можно определить через суммарный расход материала

, (283)

где Q- расход материала; L- длина валка.

Подставим u из выражения (282) в уравнение (283) и проинтегрируем его в приделах интегрирования от до . В результате интегрирования получим

. (284)

В то же время суммарный расход материала, проходящего через зазор :

. (285)

Так как расход материала, проходящего через любое сечение зазора в единицу времени, одинаков, то, приравняв правые части уравнений (284) и (285), получим

. (286)

Как видно на рис.40, зазор . Экспериментально установлено, что в большинстве случаев .

Подставляя dp/dy в выражение (282) и воспользовавшись для облегчения выкладок безразмерными параметрами и , получим окончательное выражение для расчета скорости потока материала

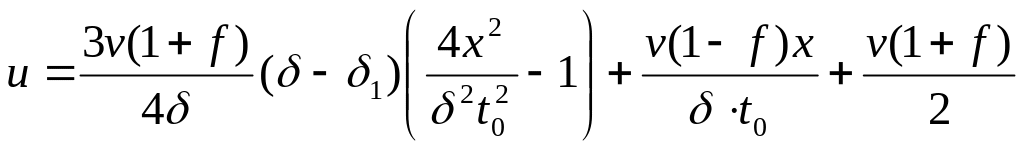. (287)

Это уравнение описывает распределение скоростей частиц потока в поперечном сечении зазора валков, имеющих разную угловую скорость. Интересно отметить, что скорость потока не зависит от природы материала.

В гидродинамической теории постулируется пропорциональная зависимость между коэффициентом вязкости и градиентом скорости. Среднее значение эффективной вязкости может быть найдено из уравнения (285) для определения распорных усилий при условии, что на участки длинны рабочего канала, на котором действуют эти распорные усилия, известно средние значение градиента скорости.

Дифференцирование зависимости (287) дает градиент скорости в сечении межвалкового зазора в виде

. (288)

Интегрирование этого уравнения в интервале от сечения, в котором происходит захват материала (рис. 41), определяемого параметром

, (289)

до выходного сечения, в котором и

дает среднее значение градиента скорости.

Однако при определении среднего значения градиента скорости следует иметь в виду, что часть функции (288) находится в отрицательной области. Поскольку вязкость не может быть величиной отрицательной, а распорные усилия представляют собой результат интегрирования функции давления, положительной на всем интервале интегрирования , то для нахождения среднего значения градиента скорости применяют теорему “о среднем”, согласно которой

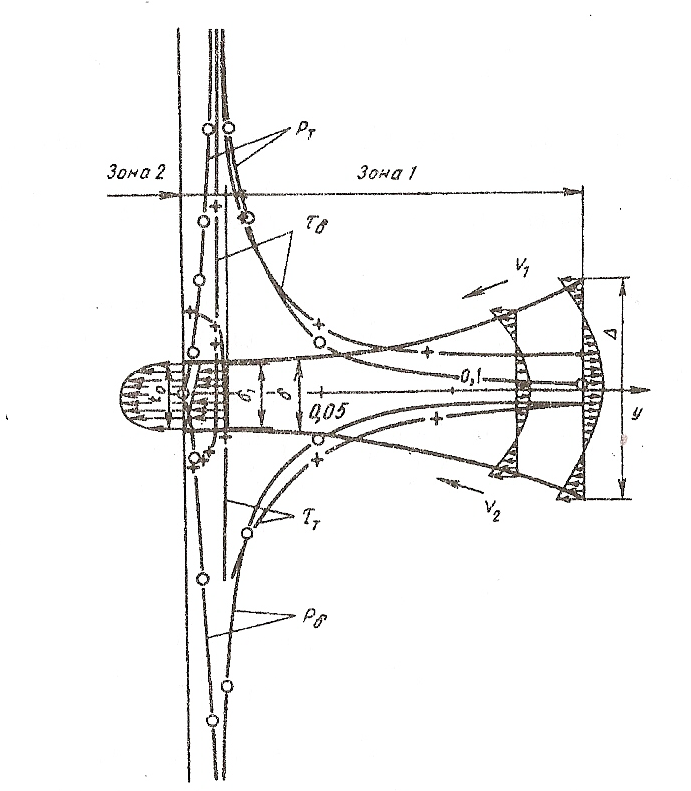
Рис.41. Распределение поля скоростей ( ), давления p(0-0), напряжения сдвига (+ - +)

в рабочем канале вальцев при обработке керамической массы, реологические свойства которой характеризуются параметрами ,

. (290)

Таким образом, уравнение (290) нужно интегрировать на двух отрезках функции: от до и от до и сум­мировать полученные значения по абсолютной величине (см. рис. 41).

В интервале от до в результате интегрирования уравнения (288) на поверхности быстроходного валка по дуге получим

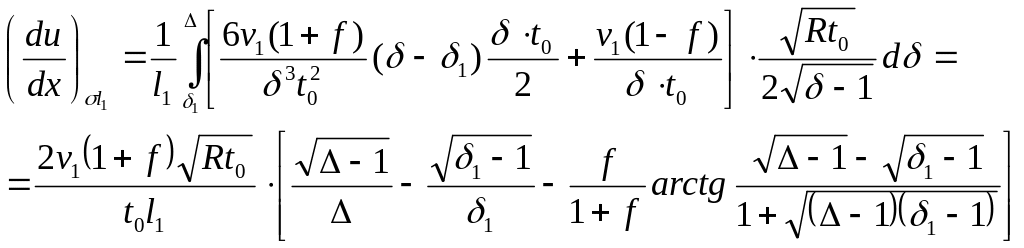(291)

В интервале от до в результате интегрирова­ния уравнения (288) на поверхности валка по дуге получим

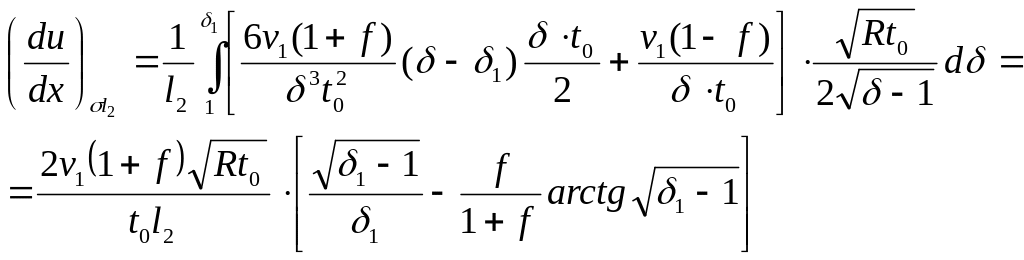(292)

Соответственно для тихоходного валка

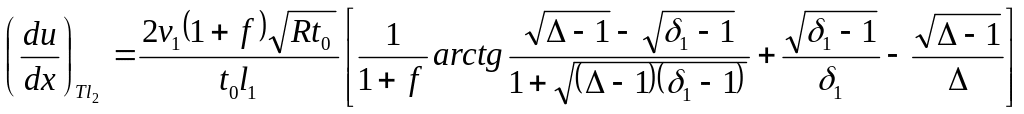; (293)

. (294)

Давления в зазоре валков определяют путем замены у в уравнении (286) параметром t. Из треугольника О1ВС (см. рис. 40) имеем

. (295)

В то же время х можно определить как

. (296)

Подставив значение х из уравнения (296) в уравнение (295), получим

,

откуда

. (297)

Разложим выражение, стоящее под знаком радикала, в ряд. Пренебрегая членами высшего порядка, получим

. (298)

Продифференцируем левую и правую части этого урав­нения, откуда

. (299)

Подставив у из уравнения (298) в уравнение (299), получим

, (300)

где знак « + » соответствует случаю, когда у > 0, а знак « - », когда у < 0.

Заменим переменную t в уравнении (300) ее значением

(301)

Подставив в уравнение (286) значение dy из выражения (301), получим

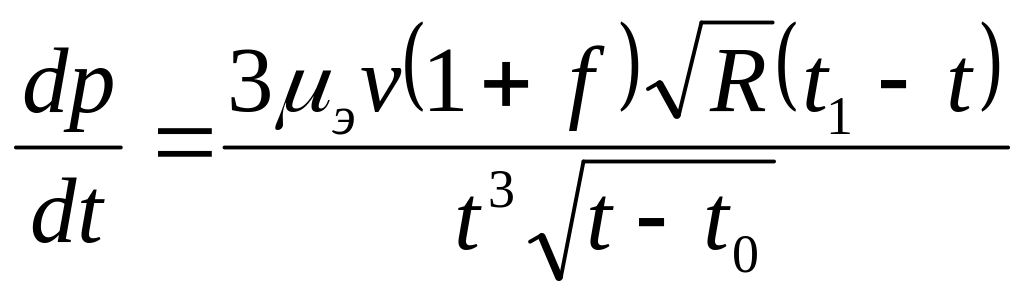. (302)

Проинтегрируем выражение (302) в пределах от Т до t₀. После преобразований выражение для определения давле­ния в зазоре валков принимает вид

. (303)

Из зависимости (303) видно, что давление в значительной мере зависит от величины зазора (с уменьшением зазора оно быстро увеличивается).

Распорное усилие на валки в общем случае определяют суммированием элементарных давлений в рабочей зоне валков:

. (304)

Подставляя значение р и dy из выражений (303) и (301) в уравнение (304) и решая его, получим окончательное урав­нение для определения распорного усилия

. (305)

Здесь для определения значения можно ориентировоч­но найти градиент скорости по формуле

. (306)

Рассчитаем мощность, исходя из затрат энергии на сжа­тие материала, поскольку керамическая масса, двигаясь в зоне дуги захвата под действием сил трения, преодолевает сопротивление сил нормального давления. Если заменить действие сил трения равнодействующей Т, приложив ее к воображаемому концу ленты керамической массы, выходя­щей из зазора t₀, то формулу для работы А, затрачиваемой на сжатие керамической массы согласно теории прокатки, раз­работанной акад. А.И. Целиковым, можно записать в виде

, (307)

где - отношение распорных усилий к площади рабочей поверхности валка; (l - длина дуги захвата ма­териала); b - ширина валка; - абсолютная деформация материала; - длина ленты материала после прохода через зазор валков; ; - объем ленты материала.

Учитывая, что истинная деформация материала

,

уравнение (307) можно записать в виде

.

В свою очередь работа, совершаемая при деформации ма­териала за один оборот валков, может быть представлена как

. (308)

В то же время

, (309)

где t - время одного оборота, с; n - частота вращения валка, об/мин.

Подставив значения А из выражения (308), Р из выраже­ния (305) в формулу (309), получим

(310)

где - среднее значение вязкости материала; l - дуга за­хвата материала.

Таким образом, мощность, потребляемая тихоходным валком

; (311)

для быстроходного валка

. (312)