Раздел II Конструирование мельниц для помола строительных материалов Барабанные (шаровые) мельницы для помола строительных материалов

Общие сведения и классификация

Важнейшим технологическим процессом при производстве цемента, извести, керамических изделий и т. п. является измельчение различ­ных материалов до частиц размером менее десятых долей мм.

Энергоемкость процесса помола большая. Однако на измельчение материалов расходуется лишь часть энергии, потребляемой по­мольной машиной. Значительная часть ее теряется в виде тепла, звука, а также на изнашивание рабочих органов и т. д. Учитывая, что тонкому измельчению подвергаются большие массы материалов (сотни миллионов тонн), становится очевидной экономическое зна­чение совершенствования этого процесса и оборудования.

В современном производстве для помола материалов используют барабанные (шаровые и стержневые), среднеходные, ударные, вибра­ционные и струйные мельницы.

В барабанных мельницах материал измельчается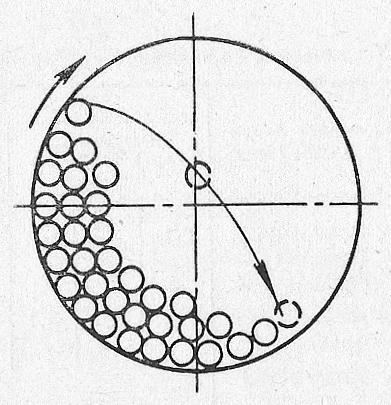

внутри полого вращаю­щегося барабана, в который помещены мелющие тела (шары, стержни). При вращении барабана мелющие тела и ма­териал (называемые в дальнейшем «за­грузкой») сначала движутся по круговой траектории (левый нижний квадрант на рис. 25), а затем, отрываясь от стен­ки, падают по параболе. Помол материала осуществляется в результате истирания при относительном переме­щении шаров и частиц материала, а также удара шаров по материалу при падении их с некоторой высоты. Рис.25. Схема движения

Барабанные мельницы классифи­цируют по режиму шаров в барабанной

работы – перио­дического (рис. 26, а) и непрерывного мельнице

(рис. 26, б–д) действия; по способу помола – сухого

и мокрого помола; по способу загрузки и разгрузки материалов – с загрузкой и разгрузкой через люк (рис. 26, а), с загрузкой и разгрузкой через пустотелые цапфы (рис. 26, б, д), с загрузкой через цапфу и разгрузкой сквозь стенки барабана (рис. 26, б).

Барабан мельницы приводится во вращение через зубчатый венец (рис. 26, е) или через центральную цапфу (рис. 26, ж).

Барабанные мельницы могут работать в открытом или замкнутом цикле. В последнем случае выведенный из мельницы материал, подвергается сортировке (сепарации) и крупные частицы (негаба­рит) возвращаются в мельницу на домол. При такой схеме работы материал, измельченный до требуемого размера частиц, непрерывно удаляется из мельницы, что повышает эффективность ее работы.

Шаровые мельницы характеризуются внутренним диаметром ба­рабана и его рабочей длиной. Некоторые технические данные бара­банных мельниц приведены в табл. 22.

Рис. 26. Основные схемы барабанных мельниц

Таблица 22

Техническая характеристика барабанных мельниц

Элемент характеристики	Тип мельниц
	Разгрузка через торцовую решетку			Разгрузка через цапфу					Трубные многокамерные
Внутренний диаметр барабана, м	2,1	2,7	3,2	0,9	1,5	2,7	3,6	4,0	2,6	3,2	4,0
Рабочая длина барабана, м	2,2	2,1	3,1	1,8	3,1	3,6	5,0	5,5	13,0	15,0	13,5
Количество камер	1								4
Мощность двигателя, кВт	160	300	600	20	100	380	1250	1500	850	2000	3200
Масса мельницы, т	41,0	66,0	95,1	4,6	18,6	81,2	162,0	170,0	160	358	411

Проектирование и расчет барабанных мельниц

Расчет критической и оптимальной угловой скорости барабана. При небольшой угловой скорости барабана циркуляция «загрузки» не будет интенсивной, так как шары, поднимаясь на некоторую вы­соту, скатываются по поверхности контура загрузки без удара. При слишком большой угловой скорости шары, находясь под дей­ствием значительных центробежных сил, не будут отрываться от сте­нок даже в верхней точке С (рис. 27), так как сила инерции Р превы­шает силу тяжести G, т. е. Р G или , откуда крити­ческая угловая скорость (рад/с)

, (195)

где g – ускорение свободного падения, м/с².

R – радиус вращения шара, м.

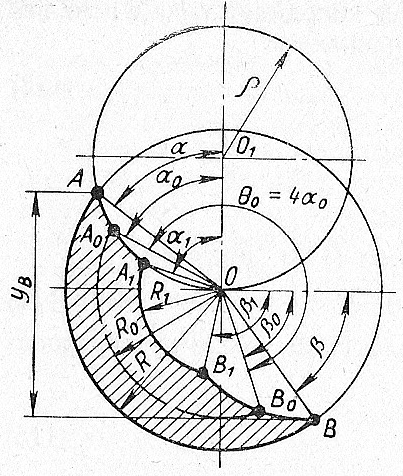
Оптимальной угловой скоростью следует считать такую, при ко­торой шар имеет максимальную высоту падения H, определяемую координатами точки отрыва шара от стенок (точка А) и точки встречи шара после падения (точка В) с окружностью барабана.

Отрыв шара от стенок в точке А будет, когда

(196)

или

. (197)

Угловая скорость при этом в рад/с

. (198)

Траектория движения шара в свободном падении представляет собой параболу (при помещении начала координат в точке А) и описывается системой уравнений

(199)

Решая совместно эту систему, найдем ординату

Рис. 27. Схема к расчету угловой точки B

скорости барабана мельницы

. (200)

Учтя, что

,

получим

. (201)

Траектория движения шаров в системе координат

(с началом в центре окружности) описывается

уравнением

(202)

Как следует из схемы (рис. 27)

;

.

Подставив эти значения в выражение (202), получим

. (203)

Заменив его значением из формулы (201), после преобразова­ний получим

(204)

Корни , соответствующие пересечению параболы с окружностью в точке А (т. е. в начале координат), равны нулю, тогда остается решить уравнение

,

откуда

. (205)

Подставив в выражение (201) значение , получим

(206)

Наибольшая энергия удара шара будет при максимальной координате . Чтобы определить максимальную координату , возьмем первую производную ее функции (206)

.

Очевидно, что и R не равны нулю, тогда

или

; .

Откуда получим, что наивыгоднейший угол отрыва шара

. (207)

Подставив значение оптимального угла отрыва в формулу (198), найдем оптимальную угловую скорость барабана (рад/с)

; (208)

здесь R, м.

Определение оптимальной загрузки барабана. Координаты точек от­рыва и падения шаров будут различными для каждого слоя шаров, поскольку они определяются соот­ношением

(209)

или

.

Обозначив получим выражение

которое является уравнением окруж­ности в полярных

Рис.28. Схема к расчету координатах. Сле­довательно, кривая (рис. 28)

контура загрузки барабан- является дугой окружности ра­диуса , описанного из

ной мельницы центра расположенного на вертикаль­ном диаметре

сечения барабана, на расстоянии от его центра.

Геометрическое место точек падения шаров (точка В) опреде­ляется соответствующим радиусом и углом . Из рис. 28 следует, что

. (210)

Преобразовав выражение (210), получим

.

Известно, что , тогда

Заменив через cos (90° – ), получим

откуда

. (211)

Величина угла для каждого слоя шаров определяется из урав­нения

.

Так можно построить контур движения загрузки и определить траектории движения шаров (рис. 28). Из анализа схемы на рис. 28 следует, что переполнять мельницу шарами также нерационально, как и недополнять. Практически шары должны занимать 0,3 – 0,35 объема барабана.

Расчет мощности двигателя барабанных мельниц. При работе барабанных мельниц энергия расходуется на подъем шаров и сооб­щение им кинетической энергии, так как после падения шаров их окружная скорость равна нулю и шары приходится вовлекать в дви­жение на каждом цикле.

Работа, затрачиваемая на подъем шаров, (Дж)

, (212)

где т — масса шаров, кг;

g — ускорение свободного падения, м/с²;

— высота подъема шаров, м.

Все слои загрузки, движущиеся на своих радиусах, заменяем одним фиктивным слоем, движущимся на расстоянии радиуса инерции от центра мельницы

, (213)

где R и — внутренний радиус барабана и расстояние от центра барабана до

внутреннего слоя загрузки, соответ­ственно (см. рис. 28).

При степени заполнения загрузкой барабана 0,3 можно принять . Тогда оптимальный угол подъема фиктивного слоя, определяемый из соотношения

с учетом, что

составит

и .

Высота подъема шаров

.

Работа, затрачиваемая на подъем шаров, (Дж)

. (214)

Кинетическая энергия, сообщаемая загрузке, (Дж)

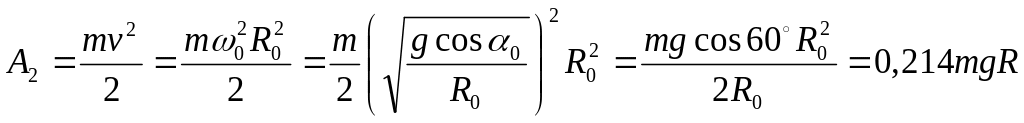. (215)

Суммарная работа, затрачиваемая на один цикл движения шаров, (Дж)

. (216)

За один оборот барабана, загрузка совершает несколько цирку­ляций.

Продолжительность одной циркуляции складывается из времени , затрачиваемого на движение шаров по круговой части траекто­рии, и времени , необходимого для движения по параболе:

.

Угол θ , соответствующий прохождению шара по парабое (см. рис. 28), при рассмотрении движения на фиктивном радиусе будет равен

θ .

Учитывая, что получим

θ .

Угол θ , соответствующий дуге, по которой шары движутся по, окружности, составит

θ .

При частоте вращения п об/с и время (с)

. (217)

Время движения по параболе (с)

. (218)

Суммарное время одной циркуляции (с)

. (219)

Число циклов фиктивного слоя загрузки за один оборот барабана

. (220)

Мощность двигателя привода барабанной мельницы, с учетом массы измельчаемого материала (принимаемой обычно равной 0,14 от массы мелющих тел), (кВт)

, (221)

где — угловая скорость, рад/с;

— к. п. д. привода;

— масса шаров, кг;

R — внутренний радиус барабана, м.

Массу загрузки (кг) можно определить по формуле

(222)

где — коэффициент заполнения загрузкой барабана ( = 0,3);

— коэффициент пустотности загрузки ( );

— плотность мелющих тел (для стальных шаров = 7800 кг/м³);

L — длина мельницы, м.

Расчет производительности трубных мельниц. Производительность барабанных мельниц, и в частности трубных, зависит от многих факторов: конструкции мельницы, состава и вида мелющих тел, свойств размалываемого материала, вида помола, тонкости измельчения и т. д.

Учесть с достаточной точностью эти факторы не представляется возможным. Поэтому после нахождения основных параметров мель­ницы производительность (т/ч) рекомендуется определять по эмпи­рическим формулам, например, по формуле ВНИИЦеммаша

, (223)

где D — диаметр мельницы «в свету», м;

— масса мелющих тел, т;

V — рабочий объем мельницы, м³;

q — удельная производительность мельницы в т на 1 кВт·ч полезной

мощности; для клинкера q = 0,035÷0,04; для известняка q = 0,05;

k — поправочный коэффициент на тонкость помола, значения которого

приведены ниже:

Остаток в % на

сите № 008 . . . 2 3 4 5 6 7 10 12 15 20

k . . . . . . . . . . . 0,59 0,65 0,71 0,77 0,82 0,86 1,0 1,09 1,21 1,42

Расчет основных деталей барабанных мельниц. Рассмотрим метод расчета на прочность корпуса мельницы и болтов, соединяющих фланцы (днища) с корпусом. Барабан мельницы рассматривается как балка кольцевого сечения, нагруженная изгибающим и крутя­щим моментами. Изгибающие нагрузки на корпус мельницы соз­даются статическими и инерционными силами.

Схема сил, действующих на корпус мельницы, показана на рис. 29.

Статические нагрузки в Н создаются силами тяжести враща­ющихся частей мельницы и загрузки , контактирующей и данный момент с корпусом

, (224)

где , и — силы тяжести корпуса с футеровкой, фланцев и диафрагм,

соответственно.

Сила тяжести массы загрузки (Н)

, (225)

где — сила тяжести шаров, Н;

— сила тяжести измельчаемого материала, Н;

— коэффициент, учитывающий, какая часть загрузки в дан­ный момент

движется по круговой траектории.

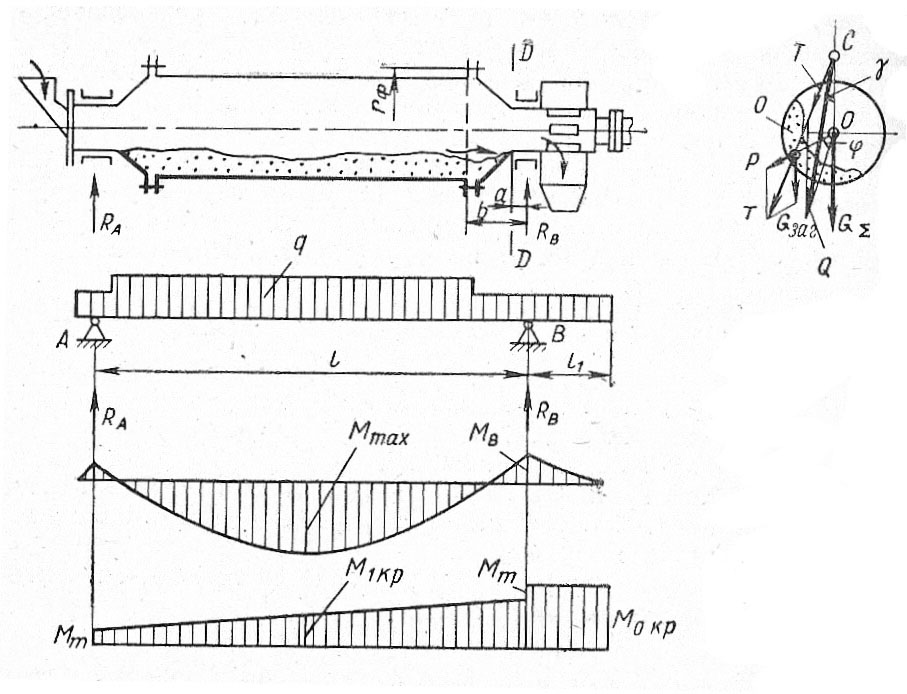
Рис. 29. Схема к расчету барабанной

мельницы на прочность

Величина этого коэффициента равна отношению времени движения шаров по круговой траектории к времени цикла [см. формулы (217) и (219)]:

.

Тогда

. (226)

Центробежная сила инерции массы загрузки, движущейся по круговой траектории, (Н)

. (227)

Учитывая, что , получим

, (228)

Точка приложения сил и Р определяется радиусом инерции загрузки (где — внутренний радиус барабана) и углом .

Равнодействующая сил и Р (см. рис. 29) в Н

. (229)

Равнодействующая сил T и (H), приложенная в точке С,

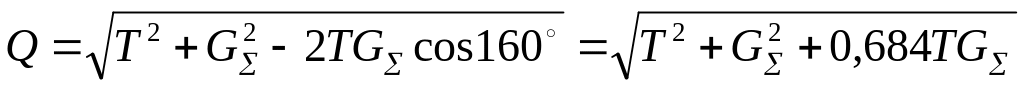(230)

(Угол между силами находим графически или по теореме синусов.)

Интенсивность распределенной нагрузки, действующей на кор­пус мельницы в плоскости равнодействующей Q, (Н/м)

. (231)

Максимальный изгибающий момент (Н·м)

, (232)

где l — расстояние между подшипниками, м.

На участке от муфты до первого (со стороны муфты) подшипника действует полный крутящий момент, подводимый к барабану, (Н·м)

, (233)

где N — мощность, подводимая к валу мельницы, кВт;

— угловая скорость, рад/с.

Вследствие трения в подшипнике крутящий момент (Н·м) умень­шается на величину

, (234)

где — нагрузка на подшипник, Н;

— коэффициент трения в подшипнике;

— радиус цапфы, м.

По длине корпуса мельницы к р у т я щ и й м о м е н т и з ­м е н я е т с я п о н а к л о н н о й п р я м о й д о в е л и ч и н ы в л е в о м

п о д ш и п н и к е.

Наиболее опасное сечение будет посредине пролета, где при­веденный момент (Н·м)

. (235)

Напряжения в этом сечении (Н/м²)

, (236)

где — коэффициент, учитывающий ослабление сечения барабана

вырезами и отверстия для болтов;

— момент сопротивления корпуса, м³;

и — наружный и внутренний диаметры корпуса.

Болты, крепящие фланцы к корпусу мельницы, устанавливают «под развертку» и рассчитывают на срез и растяжение.

Суммарная сила среза болтовых соединений (Н)

. (237)

Окружное усилие, приложенное к болтовому соединению, (Н)

, (238)

где — радиус окружности центров болтов, м.

Усилие (Н) растягивающее болты, состоит из усилия, вызывае­мого действием изгибающего момента, и усилия затяжки болтов

, (239)

где = 0,2 ÷0,3 — коэффициент, учитывающий упругость болто­вого соединения.

Усилие, растягивающее болт, вызываемое изгибающим момен­том , действующим в сечении болтового соединения, (Н)

, (240)

где — коэффициент, учитывающий неравномерность затяжки болтов;

— реакция в опоре, Н;

b — расстояние от середины подшипника до плоскости разъ­ема, м.

Усилие затяжки

, (241)

где — предел текучести материала болтов, Н/м²;

— сечение нарезной части болта, м².

Опыт эксплуатации мельниц показывает, что сечение фланца в месте перехода цилиндрической части цапфы в конусную (сече­ние D—D на рис. 29) является весьма нагруженным, поэтому не­обходимо проверить его прочность на совместное действие изгиба­ющих и касательных напряжений.

Изгибающий момент в сечении (Н·м)

; (242)

приведенный (Н·м)

. (243)

Мельницы с повышенной энергонапряженностью рабочих органов

Из учебника “Механическое оборудование предприятий строительных материалов, изделий и конструкций” В.А.Бауман, Б.В.Клушанцев, В.Д.Мартынов, издательство “Машиностроение” 1975 г. проработать стр. 125 – 131.

Мельницы ударного действия

Из учебника “Механическое оборудование предприятий строительных материалов, изделий и конструкций” В.А.Бауман, Б.В.Клушанцев, В.Д.Мартынов, издательство “Машиностроение” 1975 г. проработать стр. 131 – 142.

Струйные мельницы

Из учебника “Механическое оборудование предприятий строительных материалов, изделий и конструкций” В.А.Бауман, Б.В.Клушанцев, В.Д.Мартынов, издательство “Машиностроение” 1975 г. проработать стр. 142 – 145.

Вопросы для самопроверки и контроля

1. Назовите основные типы мельниц и их области применения.

2. Как определяется скорость вращения корпуса шаровых (барабанных) мельниц?

3. Как определяется мощность приводных электродвигателей шаровых мельниц?

4. Какие преимущества вибрационных мельниц перед шаровыми мельницами?

5. Назовите области применения мельниц ударного действия.

6. Какие преимущества струйных мельниц по сравнению с другими видами мельниц?