V. Содержание отчета
Отчет к лабораторной работе должен включать следующие разделы:
Текстовое оформление - математическая постановка задачи;
результат вычисления задачи в среде Mathcad в электронном виде;
привести точное решение аналитическим методом, привести это решение в текстовом поле в среде Mathcad, и сравнить с полученным результатом.
Привести абсолютную и относительную ошибки!
VI. Контрольные вопросы.
Какие приемы вы применили в выше приведенном фрагменте?
Почему в Mathcad применяется «прямое» написание формул?
В каком порядке располагаются выражения при написании программы вычислений?
Как изменить текстовые записи в файле Mathcad?
VII. Задачи для самостоятельного решения.
Предлагается самостоятельно изменить параметр начальных условий, чтобы посмотреть, как изменяется решение.
Измените во входных переменных параметр x .
VIII. Варианты заданий.
Условие: найти решение функции y = f(x) на отрезке [a, b] средствами Mathcad. Сравнить результат с точным значением (аналитическим решением), оценить абсолютную и относительную погрешности вычислений.
Таблица вариантов 2.1.
Численные методы линейной алгебры.
Задания.
1. Решить приближенно систему линейных уравнений А*Х = b, с точностью до 0,001 методом Гаусса. 2. Найти приближенно обратную матрицу для матрицы А, с точностью до 0,001 по схеме единственного деления.
3. Найти приближенно определитель матрицы А, с точностью до 0,0001 по схеме Гаусса.
4. Решить приближенно систему линейных уравнений А Х = 0, с точностью до 0,0001 методом Налецкого.
5. Решить приближенно систему линейных уравнений А Х = b, с точностью до 0,001 методом итераций, предварительно преобразовав ее к виду, подходящему для итераций.
Варианты к заданиям 1, 4 и 5.
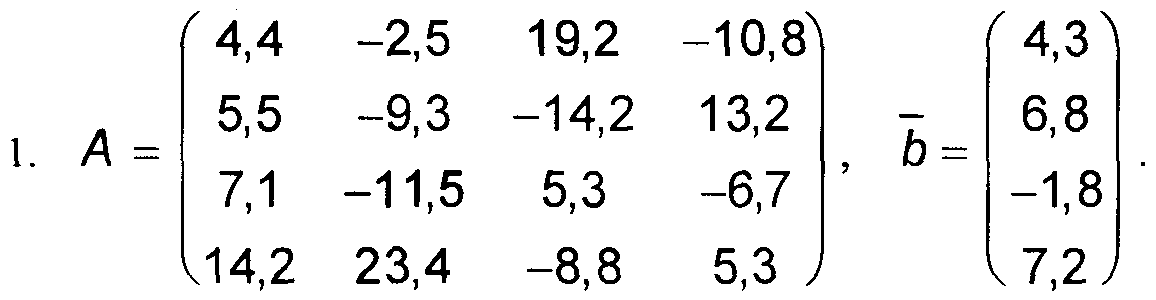
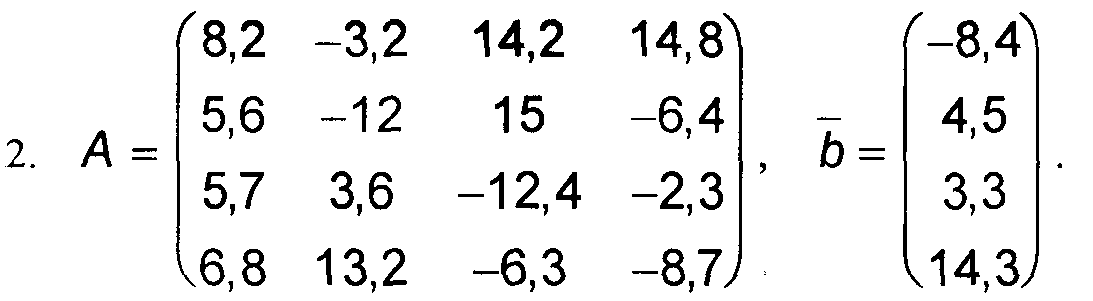
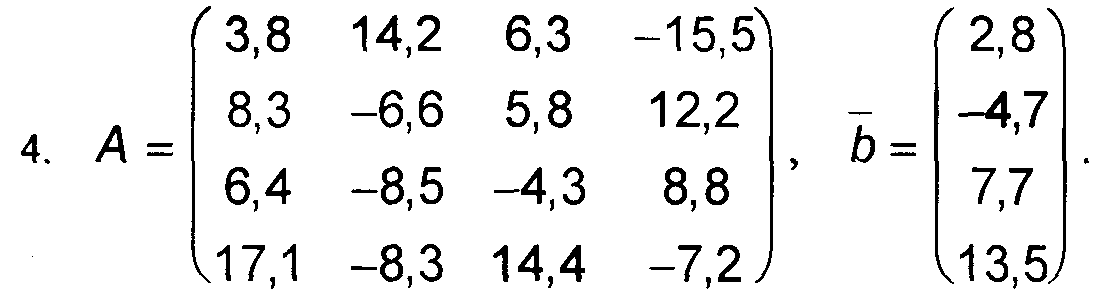
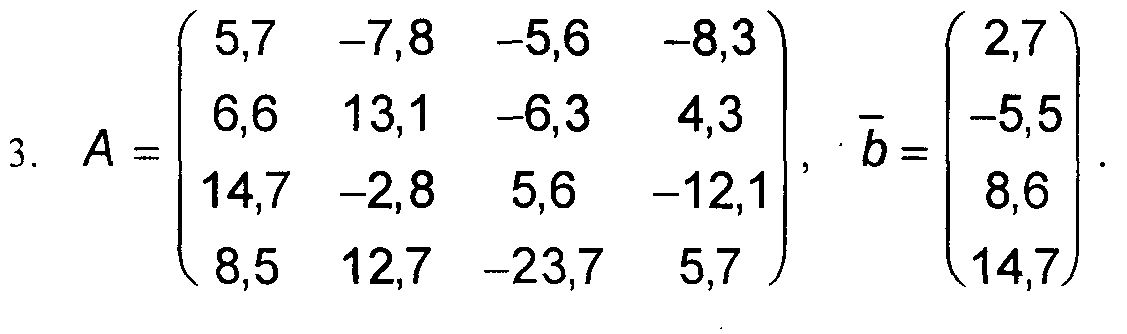
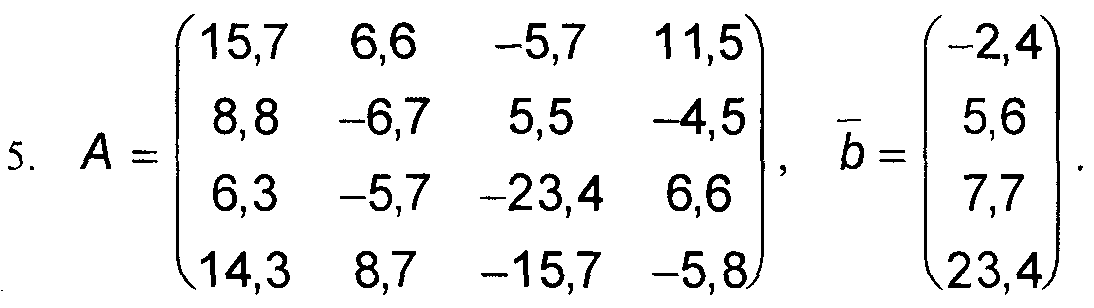
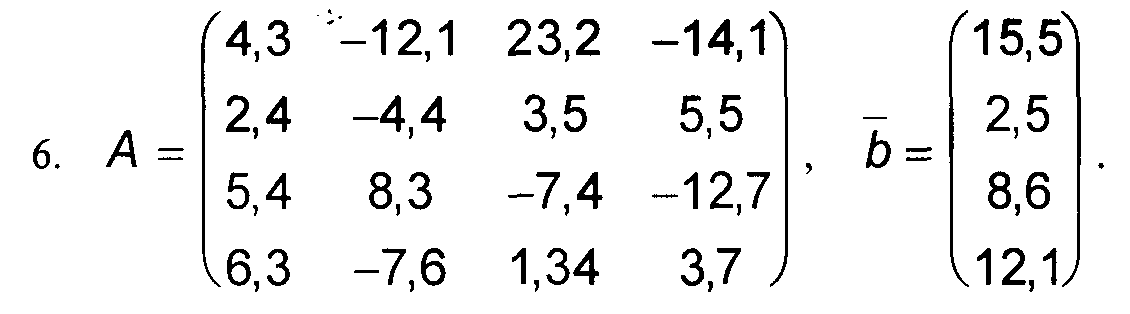
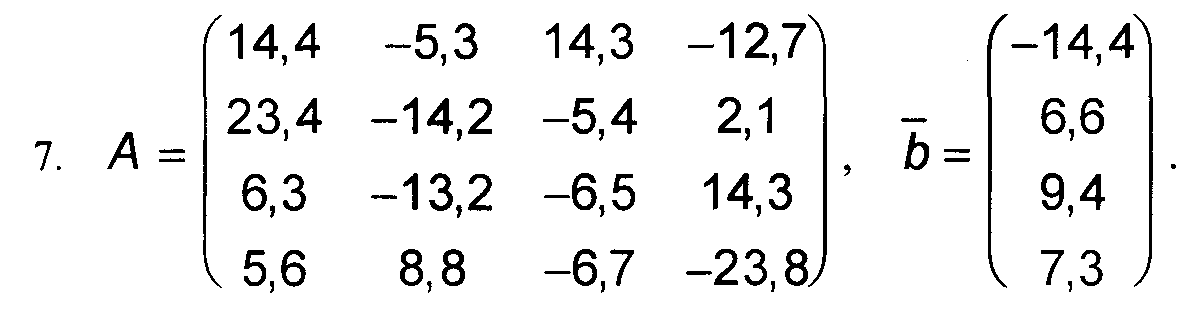
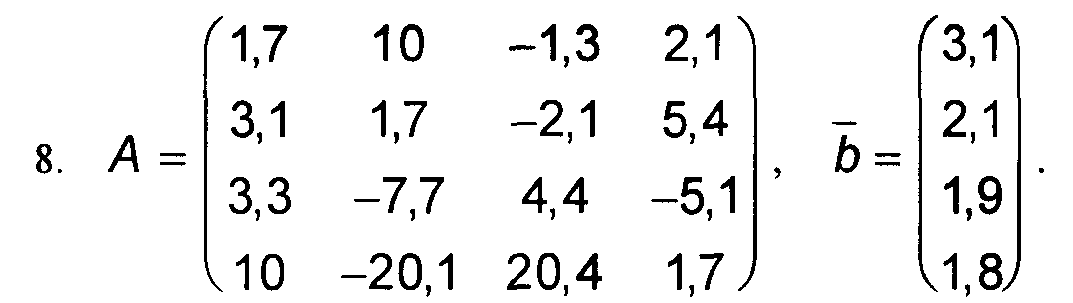
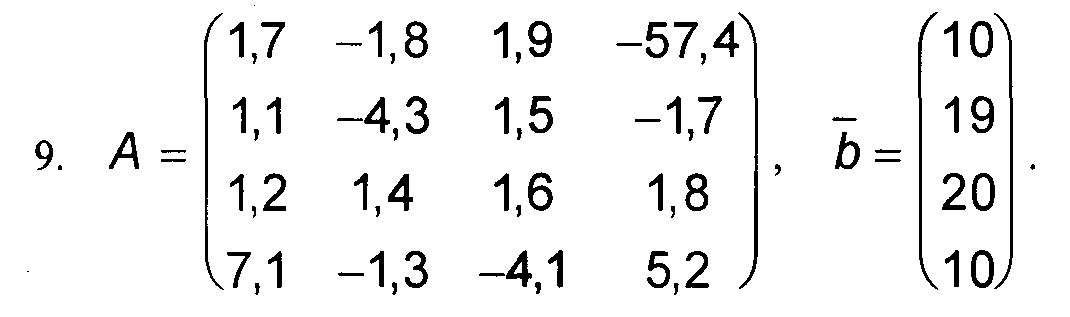
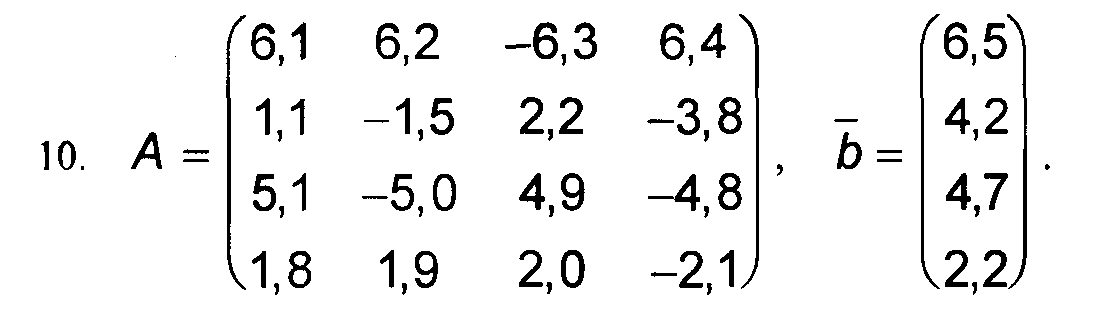
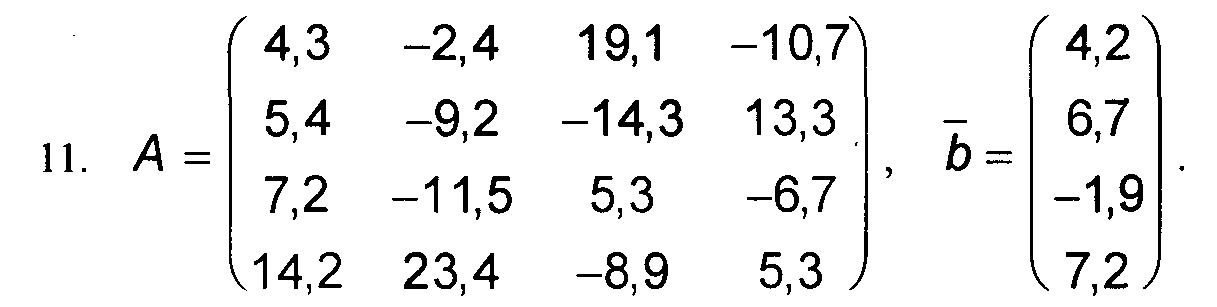
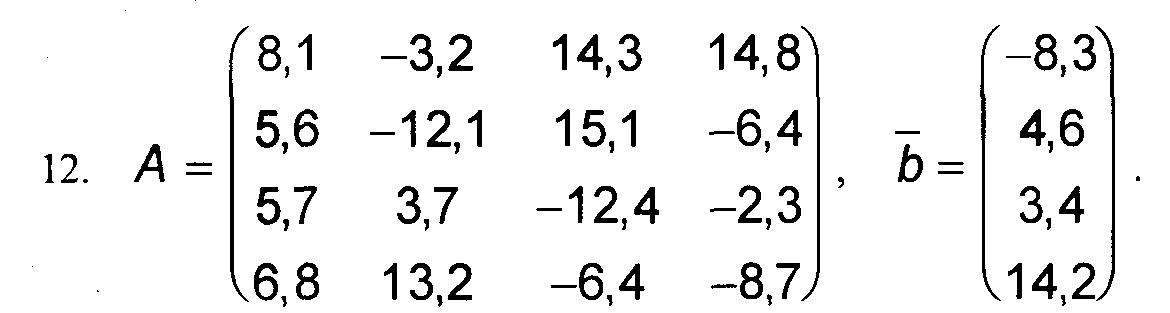
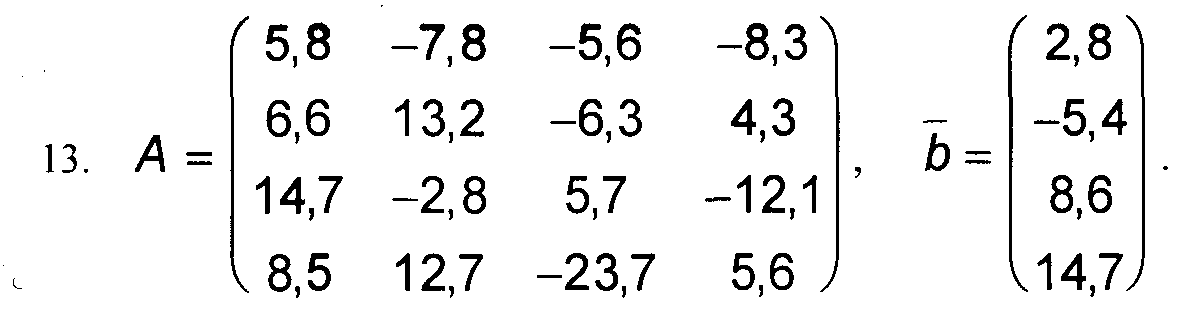
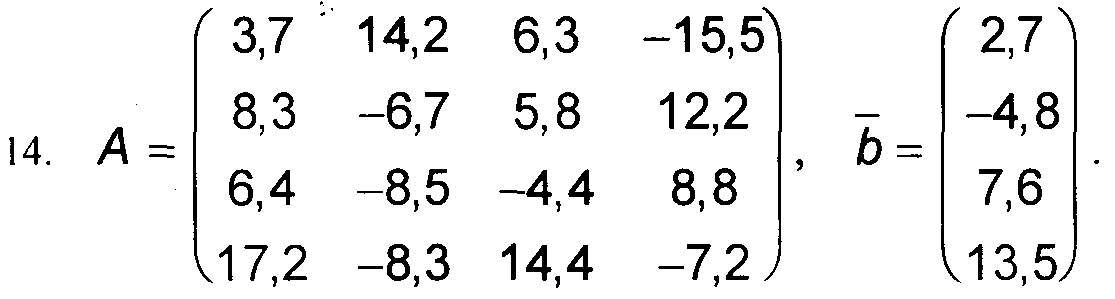
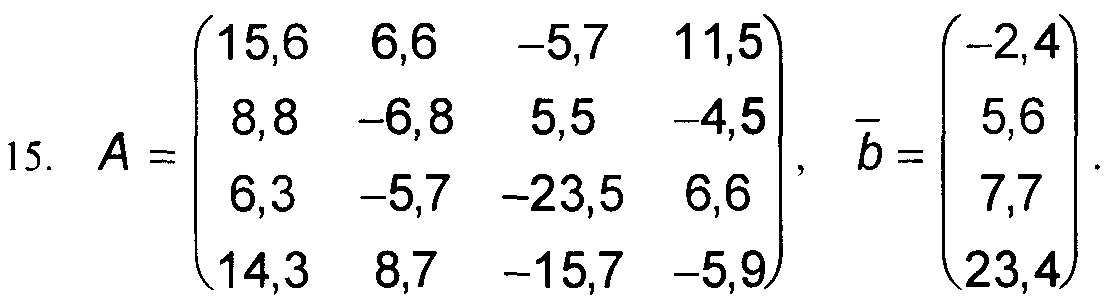
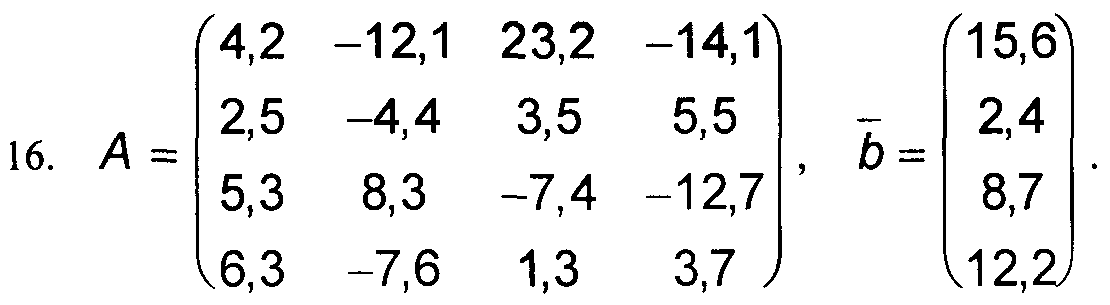
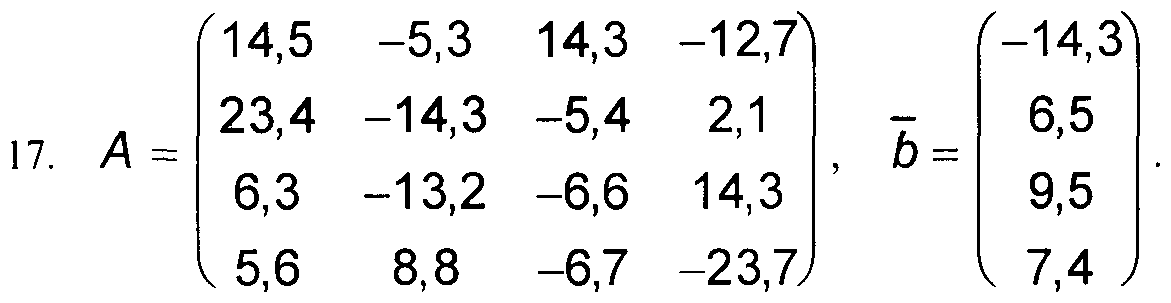
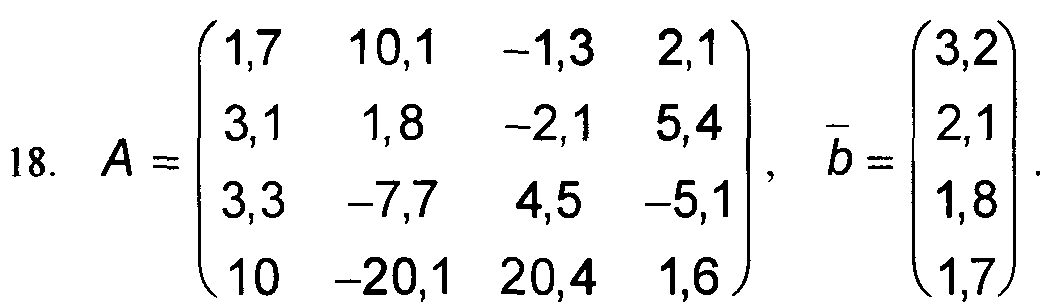
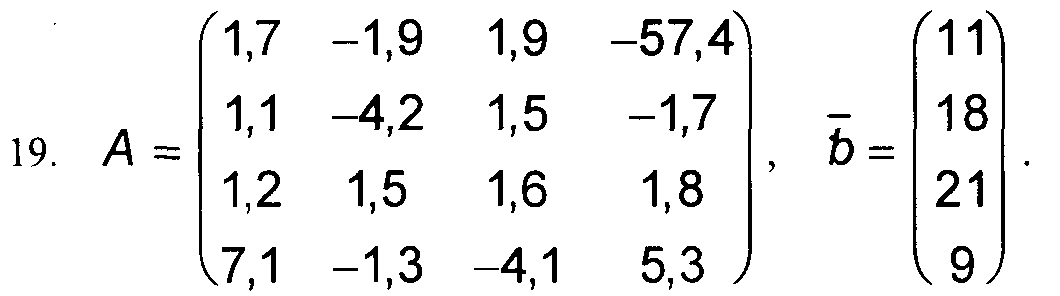
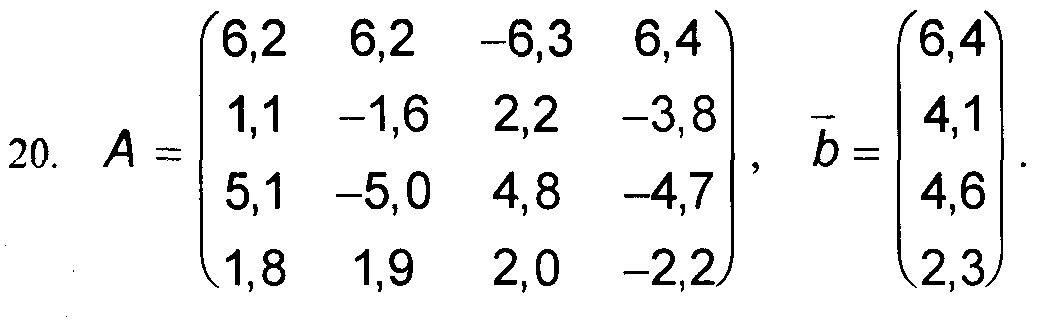
Примечание: в вариантах к заданиям 2 и 3, матрица А такая же, как и в заданиях 1, 4 и 5 (см. выше).
Лабораторная работа № 3 «Вычисления в пакете Mathcad.Интерполяция и Регрессия»
Введение.
I. Цель работы:
- освоение математического процессора Mathcad;
- приобрести умение анализа табличных данных в среде Mathcad.
II. Теоретическая часть.
Анализ экспериментальных данных.
При проведении различных экспериментов обычно требуется массив экспериментальных данных представить в виде функции, которую можно использовать в дальнейших расчетах.
Если кривая, описываемая этой функцией, должна проходить через все экспериментальные точки, операция получения промежуточных точек и расчетной функции называется интерполяцией. Если кривая, описываемая этой функцией, не должна проходить через все экспериментальные точки и является аппроксимацией (усреднением) исходных данных, операция получения промежуточных точек и расчетной функции называется регрессией.
Если необходимо уменьшить разброс данных или исключить некоторую систематическую погрешность, например, в виде наложенных колебаний, используют сглаживание данных или фильтрацию спектра колебаний данных.
Подробно о работе с массивами опытных данных рассказано в следующих лабораторных работах, здесь же приведены только наиболее удобные способы интерполяции и регрессии.