IX. Варианты заданий.
Найти вид функции y = f(x) на заданном массиве Y средствами Mathcad. Сравнить результат с точным значением (с аналитическим решением матрицы методом наименьших квадратов), оценить абсолютную и относительную погрешности вычислений.
Таблица вариантов 3.1
Вариант задания в таблице 2.1. к лабораторной работе №2. Нужно преобразовать массив 4х4 в строчный массив 1х8.
Лабораторная работа № 4 «Вычисления в пакете Mathcad»
I. Цель работы:
- освоение математического процессора Mathcad;
- приобрести навыки вычислений в среде Mathcad.
II. Теоретическая часть.
1. Решение систем уравнений.
Для решения систем уравнений надо использовать вычислительный блок (рис. 4.1.): 1. Задайте начальные приближения для всех переменных. 2. Введите ключевое слово Given. 3. Запишите систему уравнений. При записи уравнений знак равенства надо вводить не клавишей = (равно), а комбинацией клавиш Ctrl+=. Получаемый в результате жирный знак равенства = символизирует не присваивание значения, а оператор отношения.
4. Задайте ограничения на поиск решения, если они есть, в виде неравенств. 5. Введите выражение, содержащее функцию Find с неизвестными в качестве параметров.
Результат расчета — вектор решения системы. Вычислительный блок позволяет решать системы от 1 до 200 уравнений. Mathcad допускает использование двухсторонних неравенств типа
а ≤ х ≤ b. Операторы ≤ и ≥ выбираются с панели Boolean (Булевы операторы).
Решение, выданное
функцией Find,
желательно проверить,
подставив в
уравнения
найденные
корни, так
как в
зависимости от
начального приближения
Mathcad
может
вывести корни,
не имеющие
физического смысла. Так,
на рис. 4.1.
показана
проверка
решения системы
трех уравнений путем
подстановки корней
в уравнения,
построения графиков
уравнений и определения
корней как
точек пересечения
поверхностей.
На графике видна
точка пересечения
трех поверхностей,
координаты которой
являются решением
системы, обращающим
все уравнения
в тождества.
Для построения
графиков поверхностей
в нужных
пределах использована
функция
CreateMech,
которая выводит
массив значений
функции для заданных
значений аргументов.
При обычном
ускоренном построении
графика поверхности
значения аргументов
выбираются Mathcad
автоматически, что
в нашем
примере приводит
к делению
на нуль и
невозможности создания
графика. Пределы
значений
координат
нужно изменить.
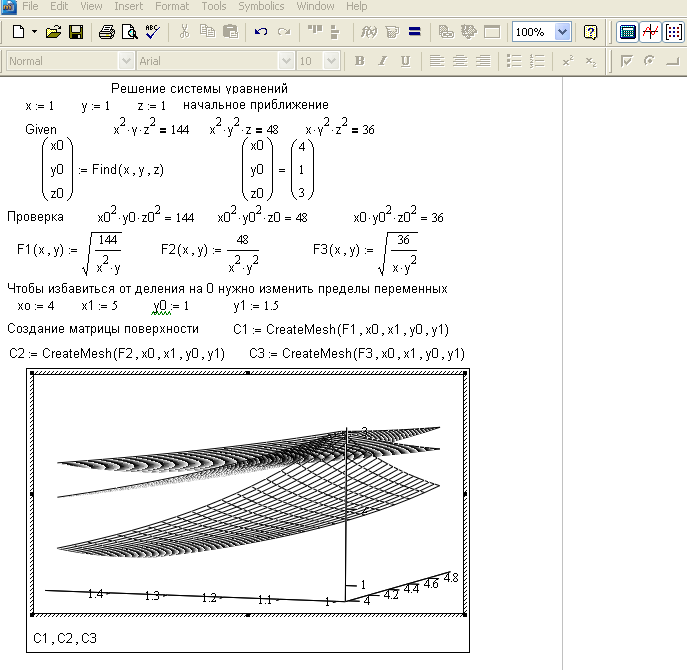
Р
ис.
4.1. Решение
системы уравнений
с помощью
функции Find
Функция Find реализует несколько градиентных численных методов, для выбора которых нужно щелкнуть правой кнопкой мыши на названии функции Find и рас- крыть контекстное меню, как показано на рис. 4.3.
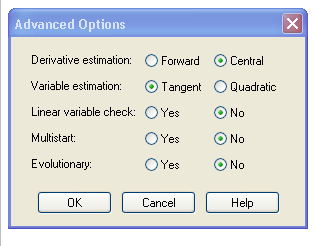
Рис. 4.2. Дополнительные опции контекстного меню функции Find.
Помимо команды Linear (Линейный метод), реализующей метод касательной, в контекстном меню имеется подменю Nonlinear (Нелинейный метод), позволяющее вы- брать один из трех нелинейных методов:
Conjugate Gradient (Метод сопряженных градиентов);
Levenberg-Marquart (Метод Левенберга);
Quasi-Newton (Квази-Ньютоновский метод).
Щелкнув на кнопке Advanced Options (Дополнительные параметры)
Рис 4.2., помимо выбора методов можно задать дополнительные параметры. Параметры оценки производной конечными разностями (Derivative Estimation):
Forward — правая двухточечная схема;
Central — трехточечная симметричная схема.
Параметры оценки переменной (Variable Estimation):
Tangent— касательная — прямая линия;
Quadratic — касательная — парабола.
Необходимость проверки линейности (Linear Variable Check):
Yes - проверять;
No - не проверять.
Если вы уверены, что нелинейности всех функций, входящих в уравнения, мало влияют на значения их частных производных, можно установить переключатель No. В этом случае производные будут считаться постоянными, что сокращает время расчета, поскольку исключает необходимость вычисления производных на каждом шаге.
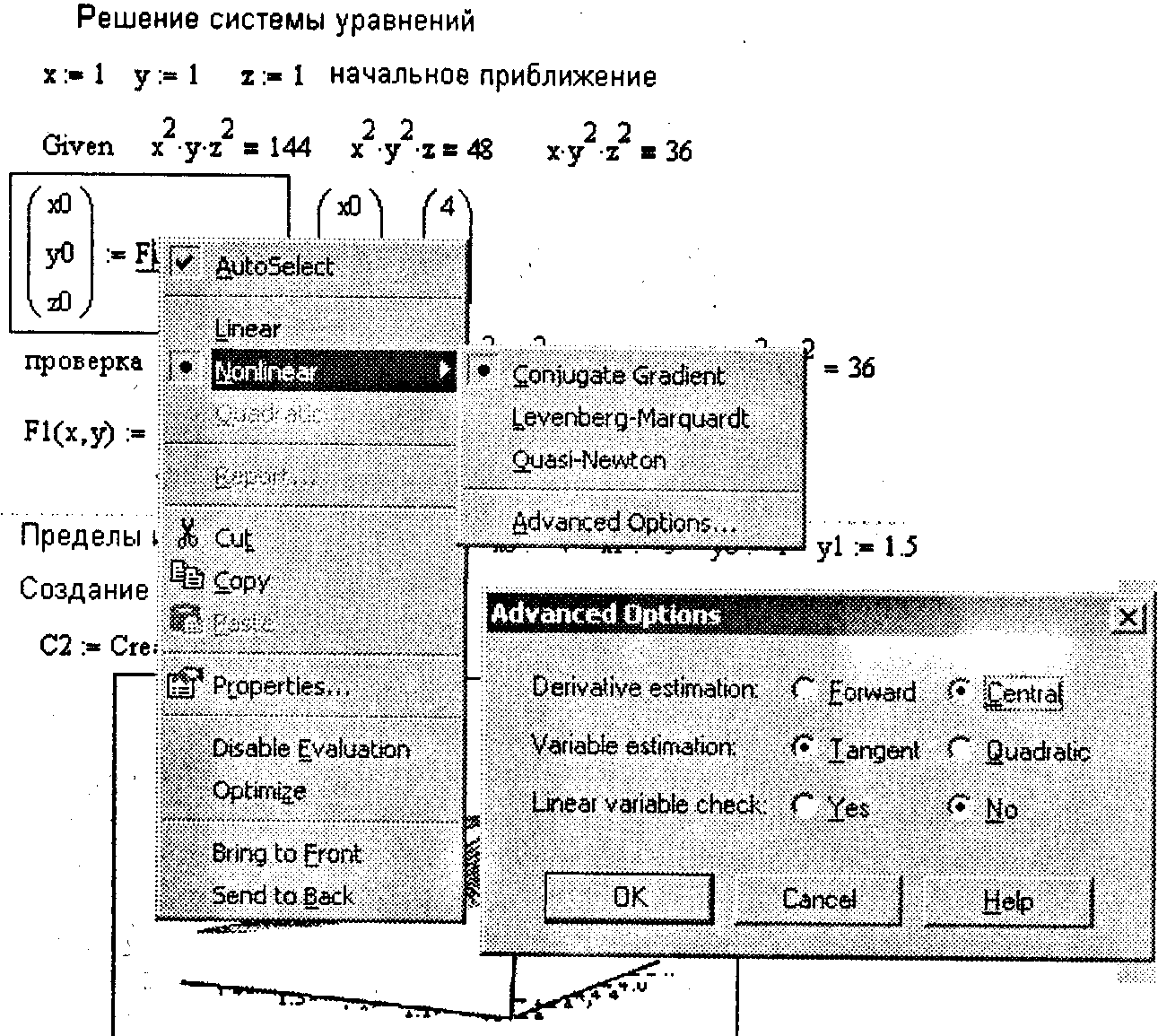
Рис. 4.3. Выбор метода решения системы уравнений
К выбору метода расчета стоит обращаться, тогда, когда Mathcad не может найти решение. В большинстве же случаев лучше доверить выбор метода Mathcad, активизировав (путем установки флажка) в контекстном меню команду AutoSelect (Автоматический выбор).
Градиентные методы, реализованные в функции Find, требуют многократного вычисления производных. Для достаточно гладких функций они обеспечивают быстрый и надежный поиск корня.
Совет: Для поиска корня негладких функций одной переменной лучше использовать функцию root, реализующую метод секущих.
Как и функция root, функция Find может включаться в функции пользователя для нахождения корней системы уравнений при переменных значениях параметров, перечисленных в названии функции пользователя. Для системы уравнений решение выводится в виде массива, каждый столбец которого соответствует вектору решения для одной переменной.
а и b - переменные параметры
начальные параметры
функции пользователя
для графика
для таблицы
это корни х и у системы уравнений
для заданных значений а и b
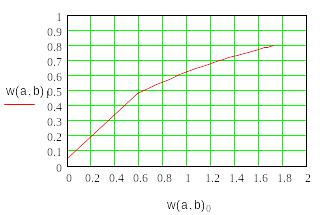
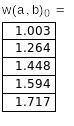
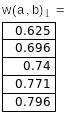
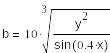
Рис. 4.4. Решение системы уравнений с переменными параметрами
Примечания: Mathcad позволяет решать системы уравнений не только в скалярной, но и в матричной форме, при этом начальные условия и ограничения задаются в виде векторов (рис. 4.4. и рис.4.5., их можно копировать прямо в Mathcad). С помощью функции Find возможно также решение систем уравнений в символьном виде.
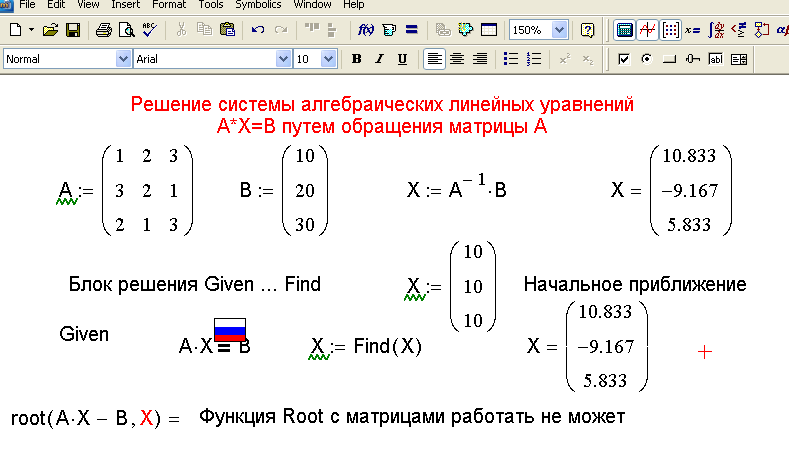
Рис. 4.5. Решение системы уравнений в матричном виде
Внимание: Блоки решения уравнений не могут быть вложенными друг в друга. Каждый блок может иметь только одно ключевое слово Given и одно имя функции Find. Внутри блока решения надо использовать не оператор присваивания (:= ), а оператор логического равенства = (жирный знак равно).
Общие рекомендации по решению уравнений
Не допускается присутствие между словами Given и Find:
других вычисляемых выражений;
дискретных переменных (х:= 0..20);
знака ≠ «не равно».
Ниже перечислены некоторые рекомендации, которым имеет смысл следовать, если Mathcad не может самостоятельно найти решение.
Возможно, точного решения не существует, и можно попытаться найти приближенное решение (см. далее).
Если корни — мнимые числа, надо ввести начальные значения в мнимой форме.
Можно поискать другое начальное приближение.
Можно увеличить или уменьшить точность расчетов. Для этого в главном меню Mathcad выберите команду Math > Options > Built-In Variables (Математика > Параметры > Встроенные переменные) и уменьшите допустимую погрешность вычислений (Convergence Tolerance(TOL)). По умолчанию TOL = 0.001.
Можно изменить ограничения в блоке Given...Find или вместо функции Find использовать функцию Minerr.
Внимательно изучите график функции (возможно попадание в локальный максимум или минимум функции) и попробуйте поискать другое приближение или добавить ограничения на поиск решения.
Посмотрите, не достигнута ли точка, из которой не может быть получено более точное решение, например, когда график функции только касается оси аргументов, не пересекая ее.