III. Магнитное поле постоянного тока.

§ 30 Магнитное поле линейного тока. Закон Био-Савара-Лапласа.

Магнитное поле обладает свойствами:

1. Образуется: а) постоянными магнитами

б) движущимися зарядами или токами

в) переменным электрическим полем

2. Действует с силой на:

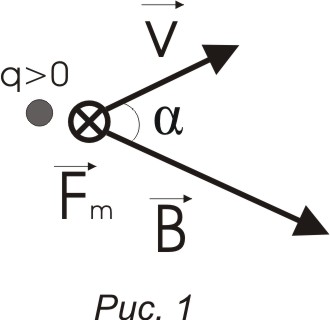а) движущий заряд или прямолинейный элемент с током (рис 1)

- сила Лоренца

- механический момент

б) действует с силой на постоянный магнит

3. Магнитное поле – это вид материи. Обладает энергией.

В любой точке пространства магнитное поле характеризуется силовой характеристикой магнитного поля В– [Тл]. Определяется как сила, действующая на прямолинейный проводник с током длины 1м. с силой тока 1А. перпендикулярно линиям магнитной индукции (рис. 2) или как момент сил Ампера действующий на рамку с током 1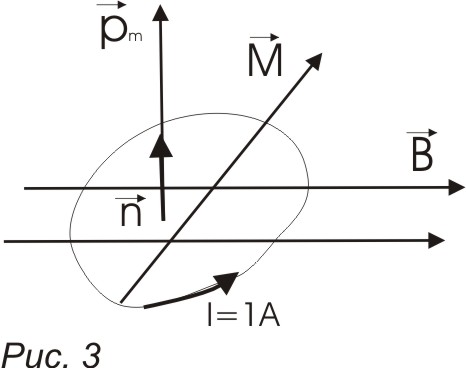 А. площади 1 м² (линии В лежат в плоскости рамки) (рис. 3).

Принцип суперпозиции.

Рассмотрим линейный ток (поперечные размеры проводника пренебрежительно малы).

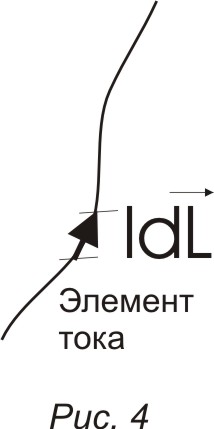Проводник разбиваем на элементы тока (рис. 4).

Для магнитного поля справедлив принцип суперпозиции:

результирующее магнитное поле нескольких токов равно сумме полей каждого из этих токов.

Магнитное поле линейных токов в некоторой точке пространства находится как вектор сумм магнитных полей, создаваемых каждым линейным током в отдельности.

или

Т.е. для нахождения магнитного поля линейного тока необходимо знать магнитное поле элементарного тока.

Закон Био- Савара- Лапласа (-Ампера)

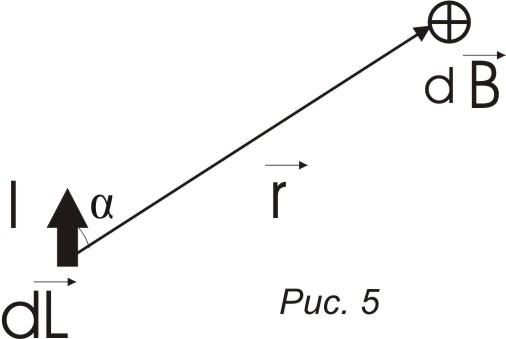
Закон Био- Савара- Лапласа (-Ампера) позволяет рассчитать магнитную индукцию элемента тока в точке А. (рис. 5)

(Для вакуума)

₀ = 410^-7 Гн/м -магнитная постоянная

_{Магнитное поле элем. тока I×dl является фундаментальным, т.к. зная магнитное поле элем. тока и принцип суперпозиции можно рассчитать магнитное поле любой системы линейных токов.}

Примеры расчета магнитных полей в вакууме.

Поле прямолинейного проводника с током

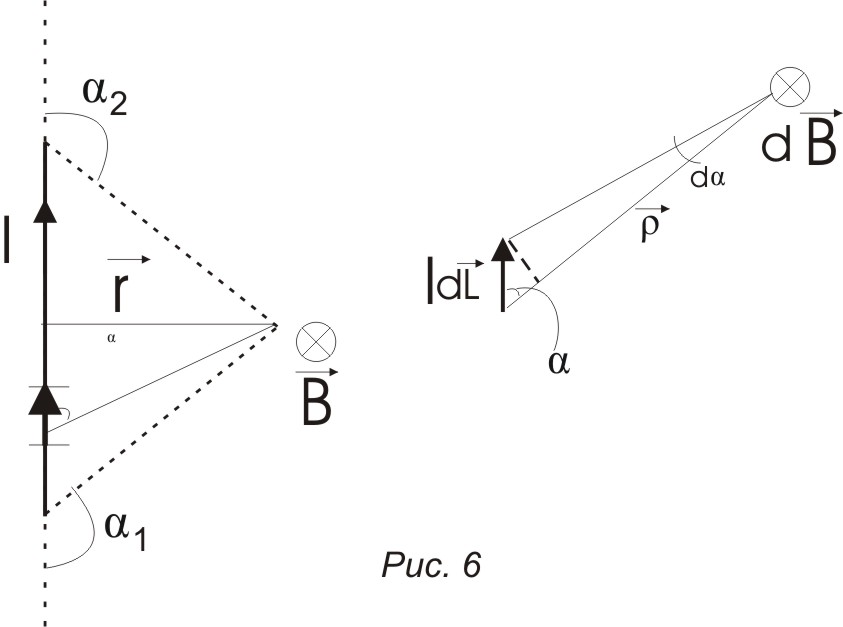
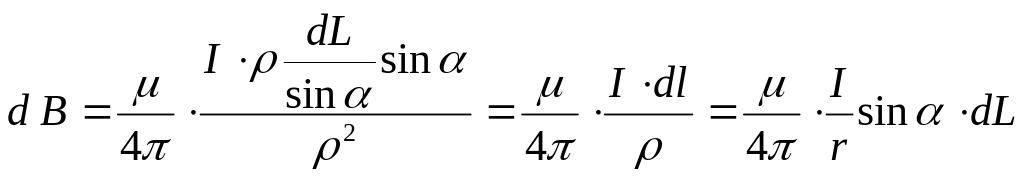
Замечание.

Для бесконечного прямолинейного проводника a₁ = 0 a₂ = p Þ

Магнитное поле кругового витка с током на оси.

Графически магнитная индукция изображается в виде линий магнитной индукции



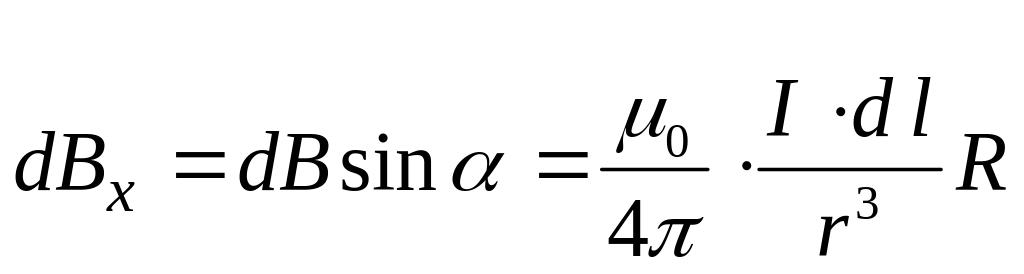
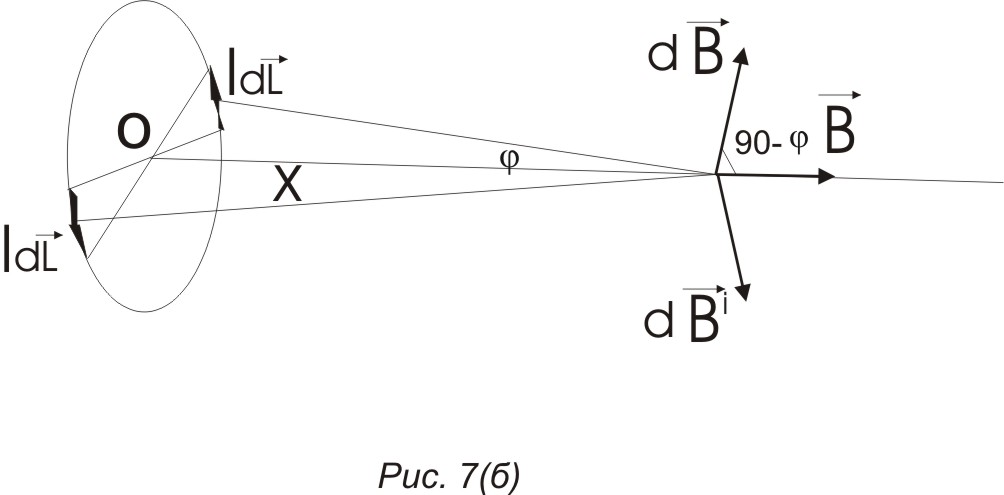
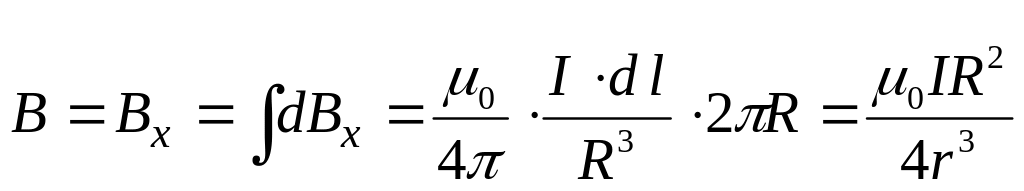
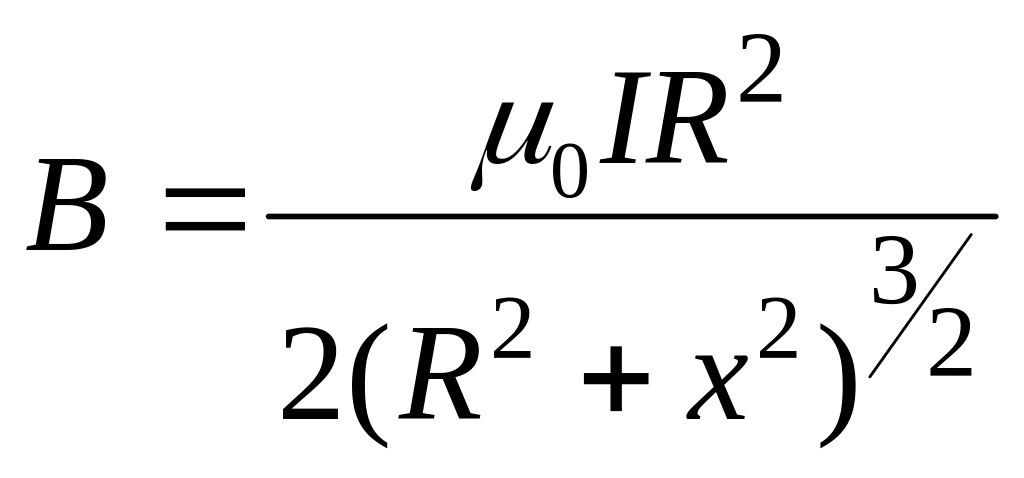
Замечание.

При х = 0 - магнитное поле в центре круглого витка.

Вихревой характер магнитного поля.

Теорема о циркуляции вектора магнитной индукции.

Электрическое поле  потенциальное поле

Магнитное поле  вихревое поле

Рассмотрим прямолинейный линейный ток.

а) натур. l совпадает с силовой линией магнитной индукции (рис.8)

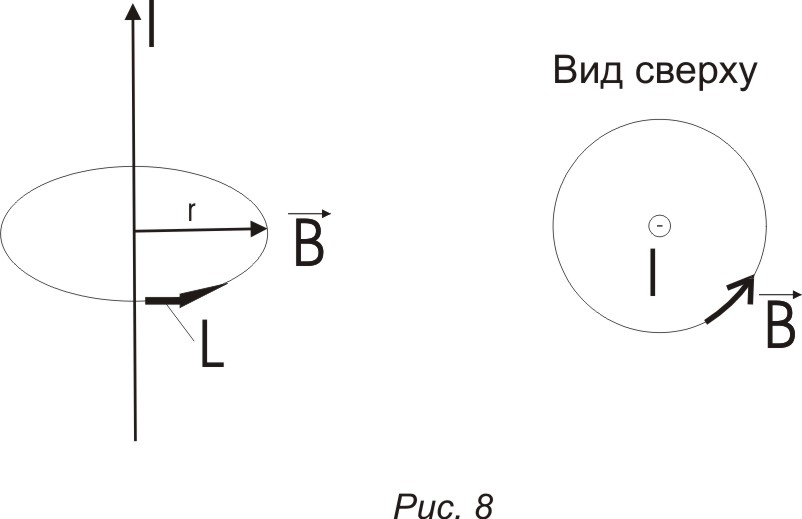
б) l – произвольный контур (рис. 9)

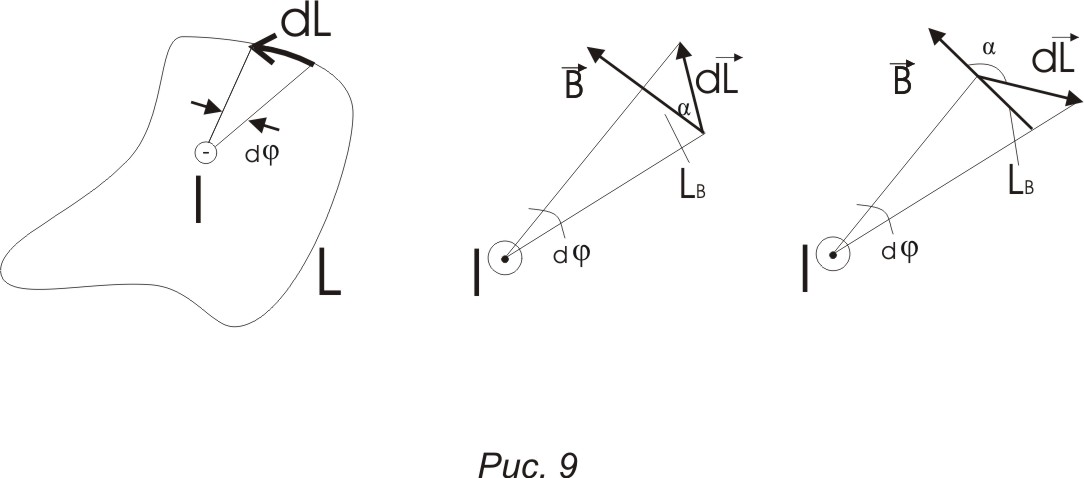
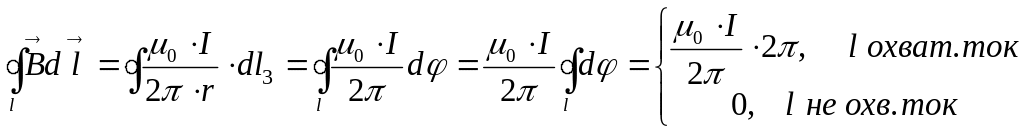
, если l охватывает ток или = 0.

Теорема о циркуляции вектора В.

Замечание 1. Знак тока в алгебраической сумме выбирают по правилу:

Если и ток I_i одинаково направлены  “+” I_i

Если и ток I_j противоположно направлены  “-” I_j

Нормаль к контуру определяется правилом правого Буравчика:

Вращать прав. бур. по направлению контура и т. д ...

П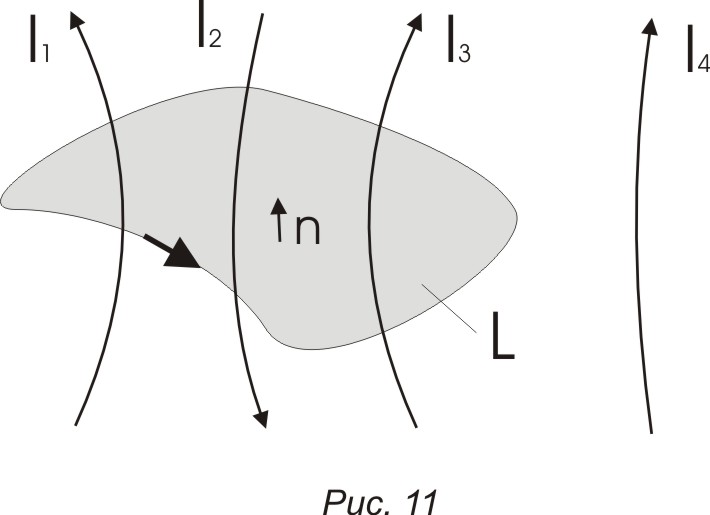 ример (на рис.11)

Зам. 2.

Иногда теорема о циркуляции вектора магнитной индукции называется законом полного тока.

Дифференциальная форма. Теорема о циркуляции .

В случае, когда проводящая среда заполняет пространство, в этой среде протекает ток распределенный определенным образом. Для характеристики используют - плотность тока. Рассмотрим замкнутый контур L, охватывающий поверхность S ,n - нормаль к контуру (рис.12).

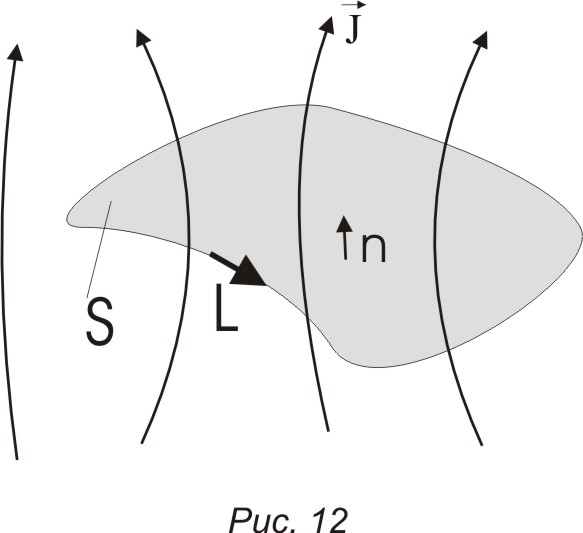
По теореме Стокса

- теорема о циркуляции в дифференц. форме

или

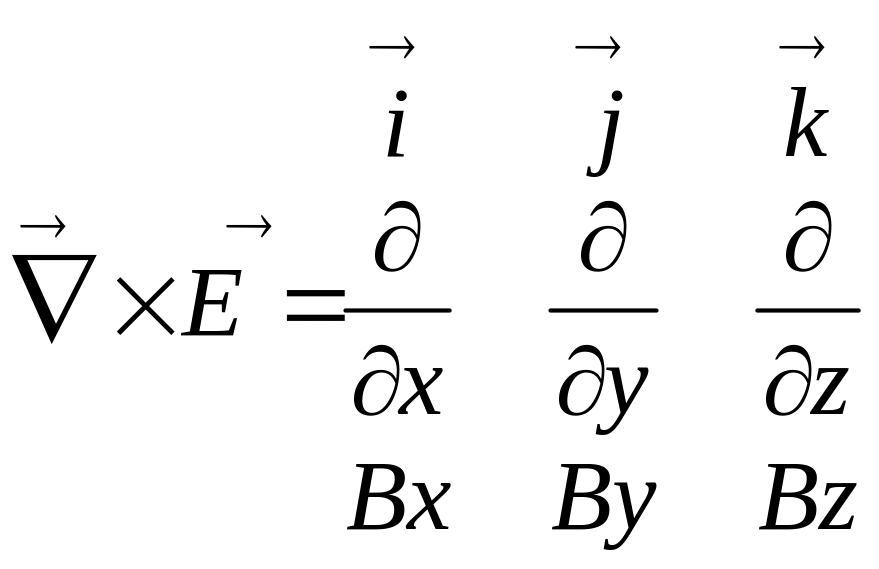
Замечание.

Ротор поля связан с в данной точке . Экспериментальная проверка – пояс Роговского.

Расчет магнитного поля линейных токов.

Наиболее распространенный расчет – метод непосредственного интегрирования, основанный на законе Био-Савара-Лапласа и принципе суперпозиции магнитных полей. Однако, для некоторых случаев симметричных конфигур. магнитных полей, когда можно выбрать замкнутый контур L таким образом, чтобы одни части контура совпадали с (линиями).

П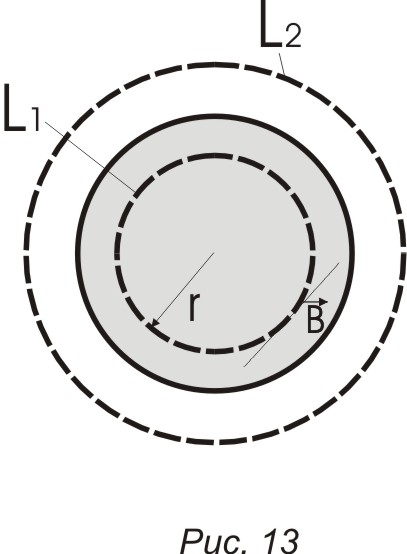 ример магнитного поля постоянного тока I, текущего по длинному прямому проводу радиуса R.

 = const

а) j =E  j = const

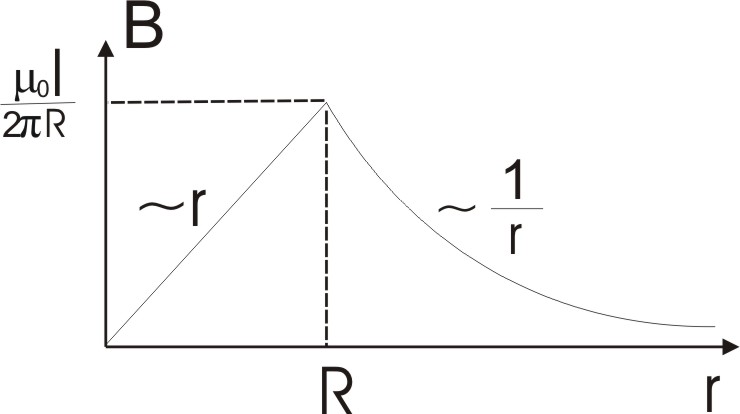
Линии магнитного поля – окружности с центром на оси провода

(левая часть)

(правая часть)

_{б) L2 – наружный провод (r  R)}

(левая часть)

(правая часть)

Пример:

Магнитное поле тороида (провод навитый на каркас, имеющий форму тора)

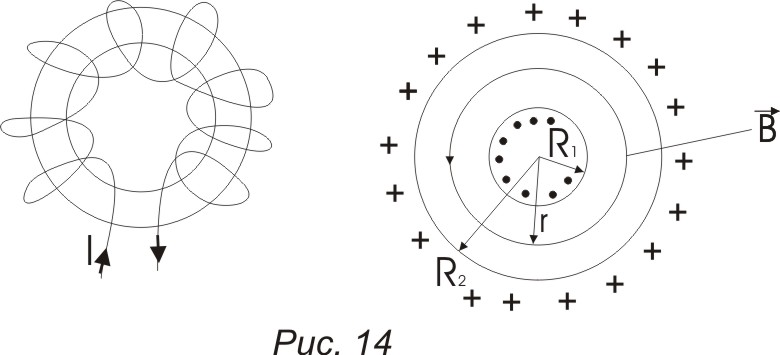
Из соображений симметрии:

а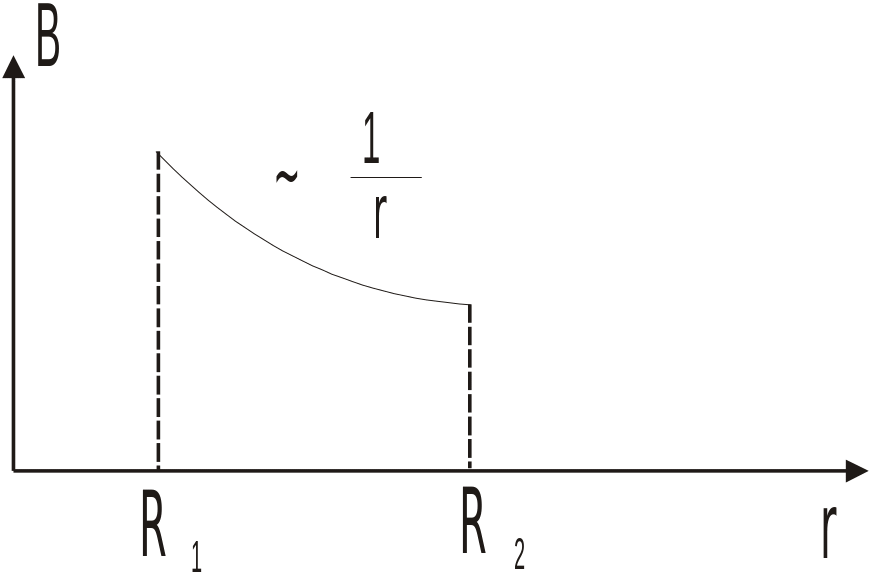 ) Силовые линии магнитной индукции - окружности

б) В = const вдоль линии L, совпадающей с силовой

(левая часть)

(правая часть)

Магнитное поле идеального соленоида.

Идеальный – без учета краевого эффекта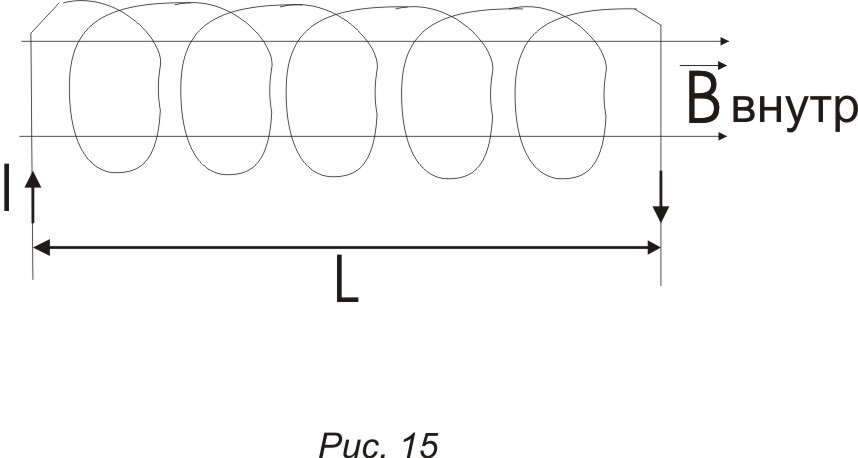

Соленоид можно рассматривать как тороид ( при R₁, R₂   ) тогда

а) поле сосредоточено внутри (В_{наружн.}= 0)

б) поле однородно

(левая часть)

(правая часть) 

Замечание.

Если тороид или соленоид будут иметь сердечники с магнитной проницаемостью , то индукция магнитного поля изменится в  раз по сравнению с вакуумом.

Теорема Гаусса для .

Магнитный поток - ….

[Ф] = Вб

Теорема:

Поток вектора через любую замкнутую поверхность S равен 0.

Теорема Гаусса для - обобщение ответа – выражает в форме постулата экспериментальный факт, что линии - замкнутые линии (число линий входящих в объем = числу линий выходящих .

Замечание.

Теорема Гаусса для вектора выражает факт, что в природе нет магнитных зарядов (т.е. нет зарядов, на которых начинаются и заканчиваются линии вектора ).

Теорема Гаусса для в дифференциальной форме.

или

Замечание.

Теорема Гаусса – фундаментальный закон для магнитного поля. Она справедлива для постоянных и переменных во времени магнитных полей.

§ 33. Сила Лоренца. Движение заряда в магнитном поле (Е = 0).

Опыт показывает, что магнитное поле порождается движущимися зарядами. Для заряда, движущегося с нерелятивистской скоростью v справедлива формула:

Закон Био-С-Л.

Т.к. электрическое поле, создаваемое зарядом, движущийся с нерелятивистской скоростью 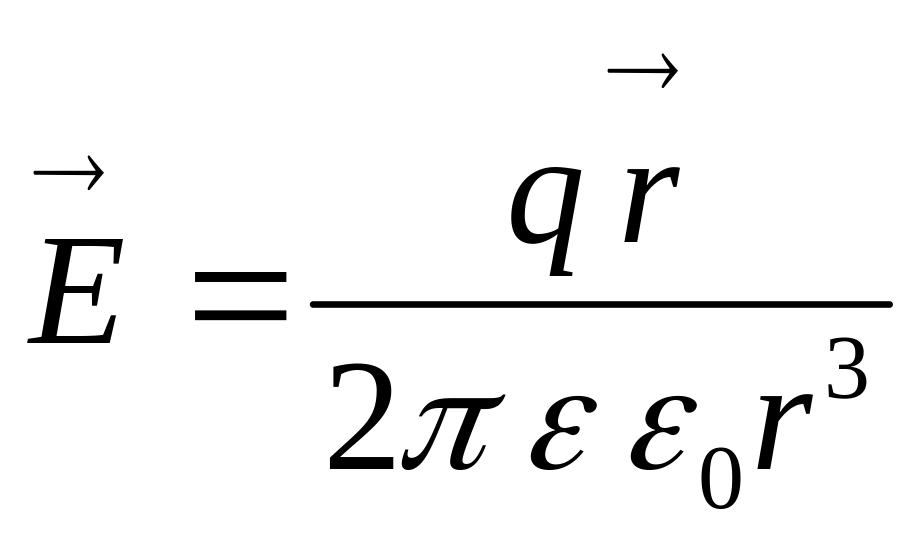, то

- электродинамическая постоянная равна скорости света в вакууме (3 10⁸ м/с).

Сила Лоренца.

Опыт показывает, что сила , действующая на заряд q со стороны магнитного поля имеет две составляющие:

а) силу - электрич. cоставляющая (не зависящую от )

б)



Сила Лоренца справедлива для постоянных и временных магнитных полей при любых скоростях движения.

Замечание.

По действию силы Лоренца на заряд можно определить модуль и направление и .

Магнитная составляющая силы Лоренца F_M   она не совершает работу и при движении заряженной частицы в магнитном поле она не может изменить Е_К, а изменяет лишь направление .