3.2.7. Задания для лабораторной работы

Решить задачи выпуклого программирования :

1. Найти минимум функции f₀(X)=x₁²+x₂²-4x₁-2x₂+5 при ограничениях f₁(X)=-x₁+2x₂ 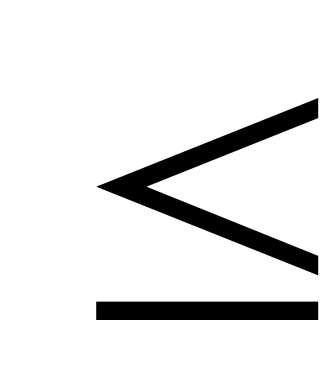1; f₂(X)=0,25x₁²+x₂² 1; 0

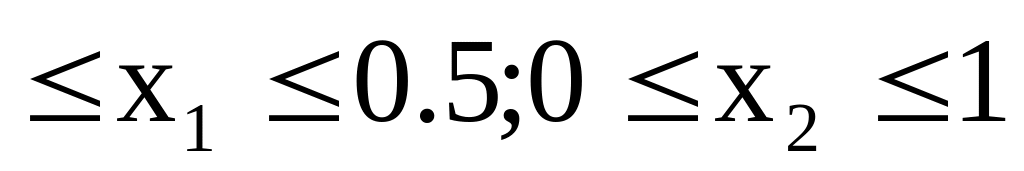
2. Найти минимум функции f₀(X)=x₁²+x₂²-16x₁-10x₂+89 при ограничениях f₁(X)=2x₁²-12x₁+9x₂ 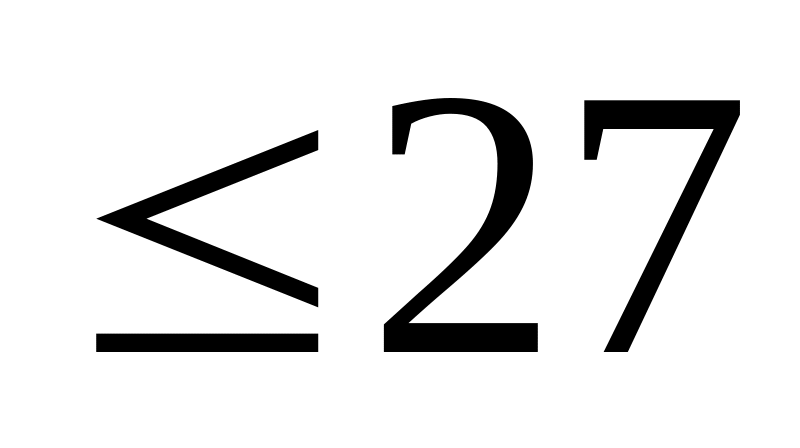;f₂(X)=5x₁²-16x₂-80 ;

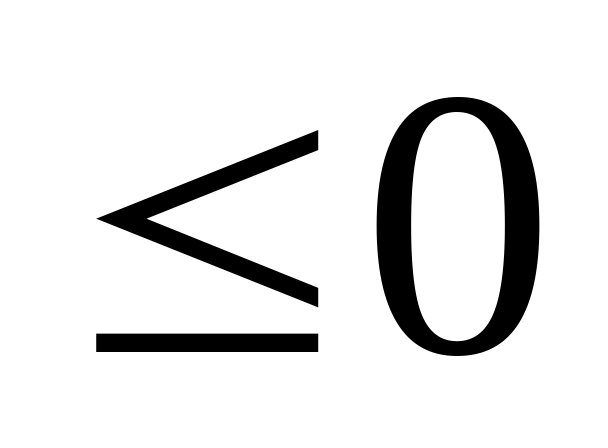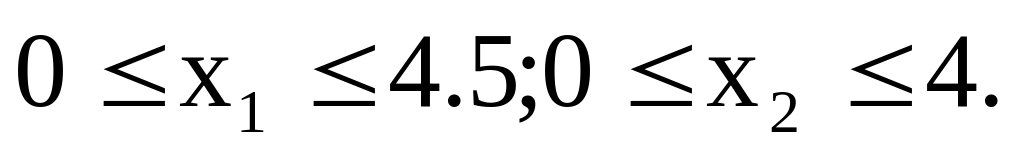
3. Найти минимум функции f₀(X)=x₁²+x₂²-14x₁-4x₂+53 при ограничениях f₁(X)=2x₁²+25x₂ 125; f₂(X)=x₁²-2x₁-4x₂ 3; 0 .

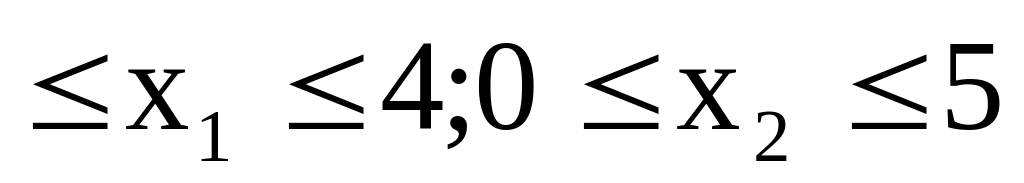4. Найти минимум функции f₀(X)=x₁²+9x₂²-10x₁-18x₂+34 при ограничениях f₁(X)=x₁+x₂ 5; f₂(X)=0.5x₁²-x₂ 4.5; 0 .

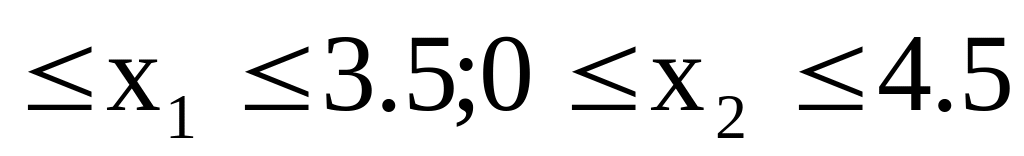5. Найти минимум функции f0(X)=x12+4x22-10x1-16x2+41 при ограничениях f1(X)=x12-4x1+x2 1; f2(X)=x12-4x1-3x2 -3; 0 .

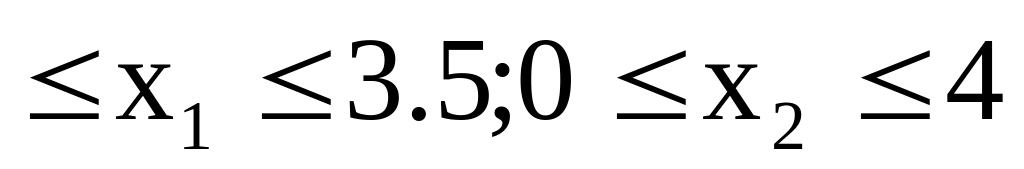6. Найти минимум функции f0(X)=x12+4x22-8x1-16x2+32 при ограничениях f1(X)=-x1+x2 1; f2(X)=2x12-4x1-x2 -1; 0 .

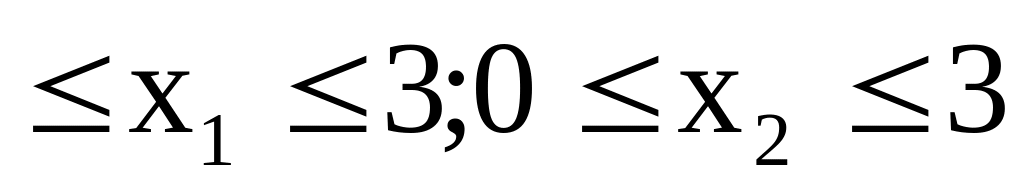7. Найти минимум функции f₀(X)=x₁²+9x₂²-10x₁-36x₂+61 при ограничениях f₁(X)=x₁²-4x₁+4x₂ 12; f₂(X)=3x₁²-7x₂ 27; 0 .

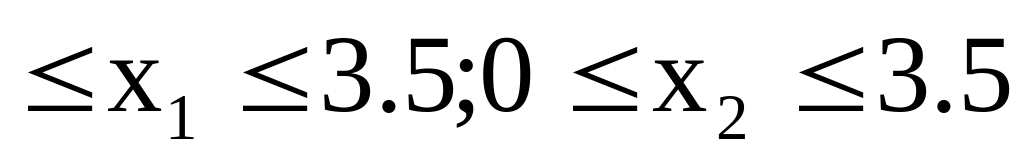3.3. Метод случайного поиска

Рассмотрим задачу условной оптимизации

min {f(X) | XR}, (3.18)

где R={XEⁿ: g_i(X)0, i=1,…,m} – допустимая область. Решить задачу (3.18) при условии непрерывной дифференцируемости функций f(X), g_i(X) можно методом штрафных функций или одним из градиентных методов, например, методом условного градиента или методом проекции градиента. Однако на практике, когда определение градиента функции f(X) затруднительно или велика размерность задачи (n и m  большие числа), предпочтение отдается методу случайного поиска.

Под названием метода случайного поиска объединяется большая группа поисковых методов, в которых для решения задачи (3.18) строится минимизирующая последовательность {X^k} из Eⁿ по правилу

X^k+1= X^k+ _k^k, k=0,1,2,…, (3.19)

где _k0 – величина шага в случайном направлении ^k; ^k=(₁^k,…, _n^k) – какая-либо реализация n–мерного случайного вектора  с известным законом распределения. Рекомендуется в качестве координат _i случайного вектора  выбирать независимые случайные величины, распределенные равномерно на отрезке [-1;1]. Таким образом, метод случайного поиска предполагает наличие датчика случайных чисел, обращаясь к которому можно получить реализацию случайного вектора  с заданным законом распределения.

В данной лабораторной работе предлагается изучить основные, наиболее употребительные варианты метода случайного поиска минимума функции f(X) на множестве REⁿ.

3.3.1. Поиск с возвратом при неудачном шаге

Этот алгоритм является простейшей реализацией метода случайного поиска. Смысл его заключается в следующем. Пусть задано некоторое начальное приближение X⁰R. Допустим, что нам уже известна точка X^kR, k0. С помощью датчика случайных чисел получим какую-либо реализацию случайного вектора ^k и в этом направлении по правилу (3.19) найдем точку

X= X^k+ ^k, (3.20)

где 0 – некоторое заданное начальное значение шага. Полученная точка X в общем случае может не удовлетворять ограничениям, задающим допустимую область R, то есть может оказаться, что XR. Тогда величину шага следует уменьшить, положив  01, и найти новую точку X по формуле (3.20) при новом значении . Описанную процедуру дробления шага повторить до тех пор, пока не выполнится условие XR. Если же этого добиться не удается вплоть до малого значения _k, то выбранное случайное направление ^k следует считать неудачным. Также неудачным считается шаг, если условие XR выполняется, но значение функции при этом не уменьшается, т.е. f(X)f(X^k). Тогда следует возвратиться в исходное состояние, положив X^k+1=X^k и совершить новый шаг во вновь сформированном направлении. Если окажется, что количество неудачных шагов из точки X^k, не приводящих к уменьшению минимизируемой функции f(X), достаточно велико, то «неулучшаемая» точка X^k может быть принята в качестве точки минимума функции f(X) в R, т.е. критерием прекращения поиска может служить выполнение соотношений

X^k=X^k+1=…=X^k+N (3.21)

при достаточно большом N.

Если сделанный из точки X^k шаг удачен, т.е. если найденная по формуле (3.20) точка XR и при этом выполняется условие f(X)f(X^k), то полученная точка X принимается за очередную точку минимизирующей последовательности, т.е. полагаем X^k+1=X и переходим к выполнению следующего этапа поиска, повторяя описанные операции в новой точке X^k+1.

Для улучшения сходимости итерационного процесса рекомендуется уменьшать начальное значение величины шага в каждой итерации по правилу _k+1_k  01.

В описанном варианте метода случайного поиска величины ₀, ,  являются параметрами алгоритма, удачный выбор которых существенно влияет на его эффективность.