Занятие 9. Интерполяция данных
Пусть у вас имеется массив экспериментальных данных, заданный таблицей X, Y. Задача по интерполяции возникает всегда, когда вы сталкиваетесь с необходимостью получить значения функции Y в промежутках между узловыми точками xi. Например, значения yi измерены с неравномерным шагом по х, а нужно получить функцию Y на равномерной сетке для последующей математической обработки. Интерполировать функцию – значит вписать другую гладкую функцию, проходящую через все узловые точки. Существует несколько различных алгоритмов интерполяции.
В LabVIEW имеется три виртуальных прибора, реализующих интерполяцию: PolyInterp.vi (полиномиальная интерполяция), RatInterp.vi (интерполяция дробно-рациональной функцией) и Spline Interpolant.vi & Spline Interp.vi (сплайн-интерполяция).
Цель работы: проинтерполировать функцию, заданную таблично, с использованием разных алгоритмов интерполяции и сравнить полученные результаты.
9.1. Задание исходного массива
О
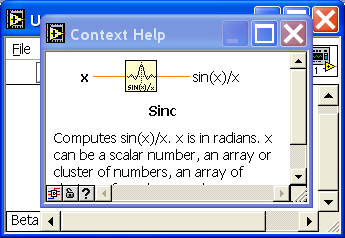ткройте
новый виртуальный прибор. Задайте
исходный массив значений X,Y.
В качестве интерполируемой функции
будем использовать функцию
.
Найдите ее в палитре Mathematics
>> Elementary
>> Trigonometric
и
поместите на блок-диаграмму.На вход узла
необходимо подать массив Х.
Его удобно сформировать с помощью Ramp
Pattern.vi
(палитра Signal
Processing
>> Signal
Generation),
который формирует массив n
линейно нарастающих значений с шагом
,
где x0
и xn–1
– начальное и конечное значения. Задайте
небольшое количество точек и диапазон
х:
–20…20.Поместите на лицевой панели XY Graph. Выведите на него график функции, как это делалось в занятии 7. Щелкните на легенде XY Graph и выберите тип графика с узловыми точками. В Properties настройте удобный вид представления XY Graph.
9.2. Использование структуры Sequence
Нам предстоит интерполировать исходный массив тремя различными способами. Чтобы компактно разместить программу на блок-диаграмме, воспользуйтесь структурой Sequence (Последовательность), которая реализуется как набор нумерованных кадров. Каждый тип интерполяции будет содержаться в отдельном кадре.
Расположите структуру Stacked Sequence на свободном месте блок-диаграммы. Добавьте еще два кадра при нажатой на рамке кадра правой кнопке (Add Frame After). Как и в случае использования других структур, данные передаются в Sequence и выводятся из нее посредством туннелей. Данные из входного туннеля доступны во всех кадрах. В то же время выходной туннель может иметь только один источник (в любом кадре). Любой кадр можно поместить под любым номером (с помощью Make This Frame…) или совсем удалить (Delete This Frame).
Замечание. В занятии 1 указывалось, что в LabVIEW реализована идеология многозадачности, т. е. обычно существует несколько параллельных потоков данных и несколько узлов блок-диаграммы могут выполняться одновременно. Иногда это может приводить к нарушению алгоритма программы. Посредством структуры Sequence в LabVIEW обеспечивается определенная последовательность выполнения программы (так называемый поток управления). Например, в экспериментальной измерительной установке нужно сначала дождаться получения данных с датчика, а потом обработать их.