5.5 Визначення прискорення вантажу по теоремі про зміну кінетичної енергії системи

Теорема про зміну кінетичної енергії матеріальної системи має вигляд

, (5.47)

де – кінетична енергія системи; - кінетична енергія системи в початковий момент часу; - сума робіт зовнішніх сил; - сума робіт внутрішніх сил.

Так як у початковий момент система перебувала в спокої, то . Дорівнює нулю й сума робіт внутрішніх сил ( =0), оскільки система, що розглядається, є незмінною. Отже, маємо

(5.48)

Система складається з п’яти тіл, із яких 3 і 4 здійснюють поступальні рухи, шківи 2 і 5 обертальні рухи навколо нерухомих осей, а коток 1 рухається плоскопаралельно.

1. Кінетична енергія тіла, яке рухається поступально рівна

, (5.49)

де – маса тіла; – його швидкість.

Для тіла 3 і 4 відповідно маємо

; (5.50)

. (5.51)

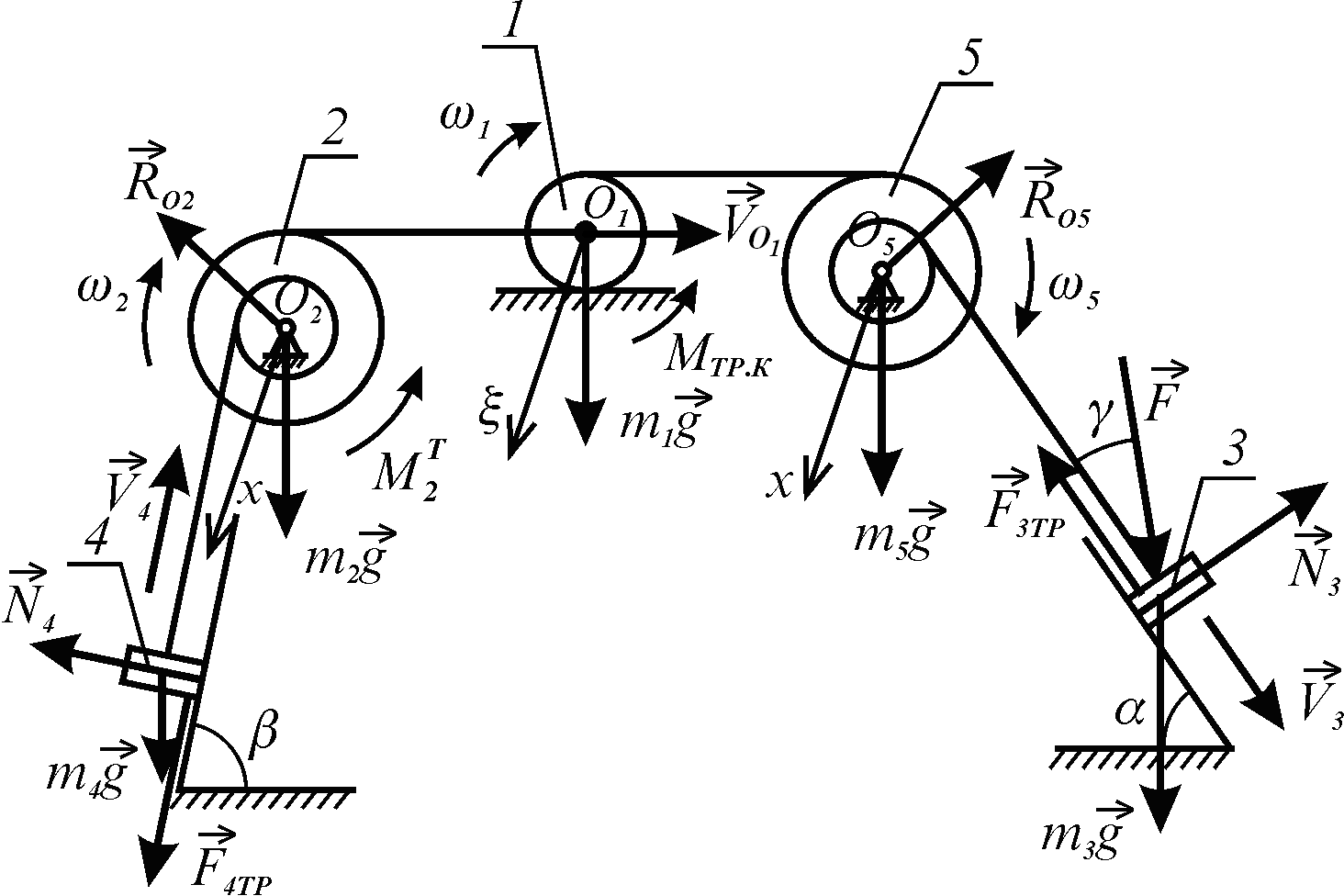
Рисунок 5.8

2. Для тіла, яке знаходиться в обертальному русі

, (5.52)

де – момент інерції тіла відносно осі обертання; – кутова швидкість тіла.

На основі (5.52) для ступінчатих шківів 2 і 5 відповідно маємо

; (5.53)

. (5.54)

3. При плоскопаралельному русі твердого тіла його кінетична енергія визначається формулою

(5.55)

Коток 1 здійснює плоский рух, отже

. (5.56)

4. Визначаємо кінетичну енергію системи, як суму кінетичних енергій ланок, які входять в систему

. (5.57)

В (5.57) підставимо (5.56), (5.53), (5.50), (5.51) і (5.54)

(5.58)

Враховуючи співвідношення (5.6)

і підставляючи їх в (5.58), отримаємо кінетичну енергію системи

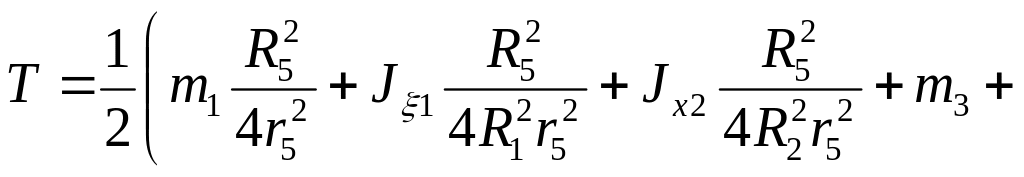
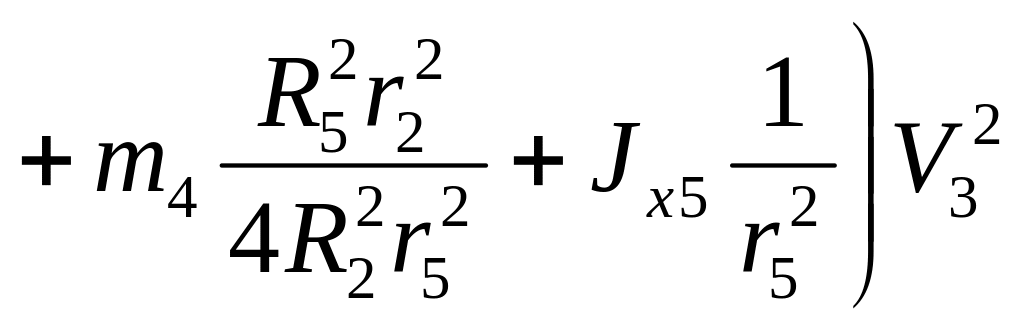. (5.59)

5. Знайдемо суму робіт усіх зовнішніх сил, які діють на систему.

На систему діють зовнішні сили , моменти та , і опорні реакції , .

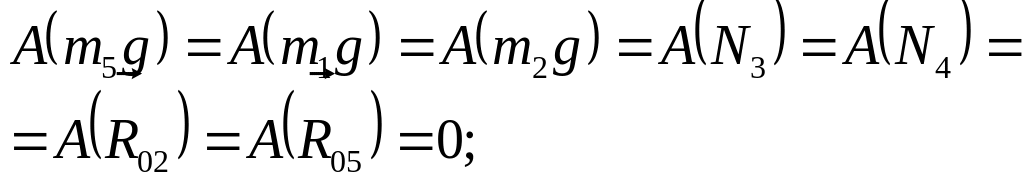
Отже,

-

. (5.60)

Підставляючи значення Т та в рівняння (5.48) та враховуючи співвідношення (5.8) отримаємо після диференціювання

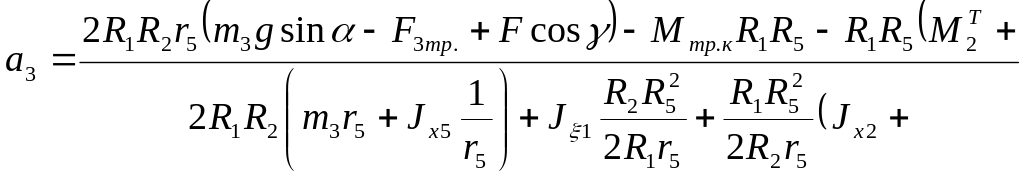
, (5.61)

що співпадає з попереднім виразом.

5.6 Визначення пришвидшення вантажу за загальним рівнянням динаміки

Загальне рівняння динаміки для механічної системи з двосторонніми ідеальними в’язями має вигляд

, (5.62)

де – задані сили, які діють на систему; – сили інерції, умовно прикладені до точок системи; – можливі переміщення точок системи.

Сили тертя віднесемо до числа активних сил.

Для розв’язання задачі даним методом необхідно знайти суму робіт всіх заданих сил і сил інерції точок системи на її можливому переміщенні. В’язі, накладені на систему є ідеальними, нитки рахуються натягнутими при роботі механізму.

1. Розглянемо систему в цілому (рис. 5.9).

Прикладемо до системи всі активні сили

і моменти та .

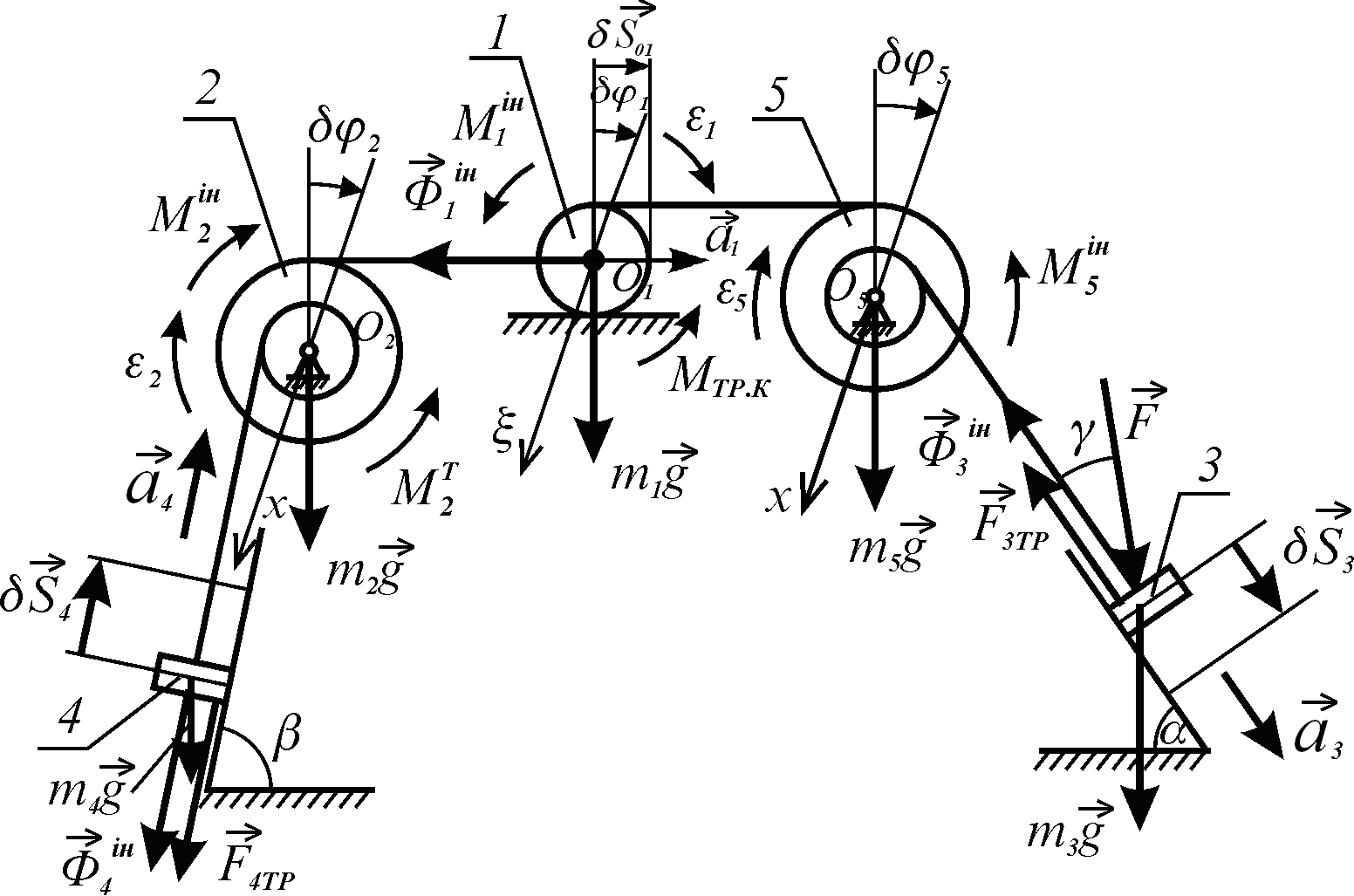
Рисунок 5.9

1.1. Сили інерції, які зумовлені прискореним поступальним рухом тіл 3 і 4 визначається формулами:

; (5.63)

. (5.64)

1.2. Сили інерції шківів 2 і 5, які обертаються навколо нерухомих осей з прискореннями і приводяться до інерційних пар, моменти яких відповідно рівні

; (5.65)

. (5.66)

Інерційні момент і напрямлені в сторону протилежну напряму кутових прискорень і .

1.3. Сили інерції котка 1, який здійснює плоскопара-лельний рух, приводиться до сили інерції, яка напрямлена в сторону протилежну і рівна

, (5.67)

а також до інерційної пари, момент якої рівний

(5.68)

і напрямлений в сторону протилежну напряму кутового пришвидшення.

2. Надамо системі можливе переміщення. При цьому вантаж 3 переміститься по похилій площині на віддаль , ланки 5 і 2 повернуться відповідно на кути вантаж 4 підніметься на віддаль . Коток 1, здійснюючи плоский рух, переміститься на віддаль і повернеться на кут . Ці переміщення показані на рис. 5.9.

Знайдемо тепер суму робіт всіх заданих сил і сил інерції на даному переміщенні системи і прирівняємо її до нуля, тобто складемо загальне рівняння динаміки

(5.69)

де згідно з співвідношень (5.7) і (5.8)

(5.70)

3. Підставимо (5.70) в (5.69) і визначимо .

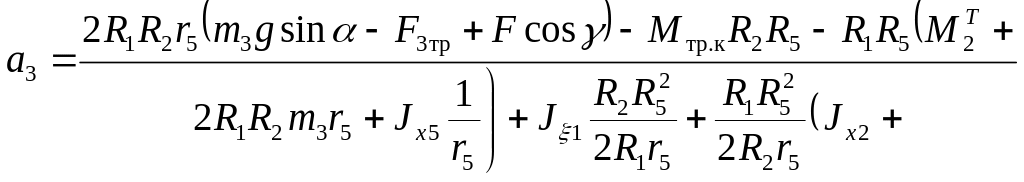
(5.71)

що співпадає з попереднім виразом.