
- •Предисловие
- •Занятие 1.Понятие функции, предела и непрерывности функции. Производная функции
- •Краткие сведения из теоретического курса Понятие функции
- •Определение предела функции и бесконечно малой функции
- •Основные теоремы о пределах
- •Производная функции
- •Производная сложной функции
- •Занятие 2.Дифференциал функции. Производные и дифференциалы высших порядков. Применение производных к решению прикладных задач
- •Дифференциал функции
- •Геометрический смысл дифференциала функции
- •Производные высших порядков
- •Механический смысл производной второго порядка
- •Дифференциалы высших порядков
- •Приложение дифференциального исчисления
- •Производные и дифференциалы функции нескольких аргументов
- •Основные понятия
- •Частные производные и дифференциалы функции нескольких переменных
- •Полный дифференциал функции
- •Частные производные второго порядка
- •Решение задач
- •Неопределенный интеграл и его основные свойства. Основные методы интегрирования.
- •Основные понятия
- •Свойства неопределенного интеграла
- •Метод непосредственного интегрирования
- •Метод замены переменной (подстановки)
- •Метод интегрирования по частям
- •6. Задание на дом.
- •Определенный интеграл и его основные свойства. Приложения определенного интеграла.
- •Определенный интеграл как предел интегральной суммы
- •Свойства определенного интеграла
- •Геометрический смысл определенного интеграла
- •Формула Ньютона-Лейбница
- •Метод замены переменных в определенном интеграле
- •Метод интегрирования по частям в определенном интеграле
- •Задача о площади криволинейной трапеции
- •Работа переменной силы
- •Занятие 3.Основные понятия теории вероятностей. Классическое и статистическое определение вероятности. Круглый стол «Применение математического анализа при решении задач физики, химии, фармации»
- •Понятие испытания, события, виды событий
- •Свойства вероятности:
- •Самостоятельная работа студентов на занятии
- •Занятие 4.Теорема сложения вероятностей для несовместных событий. Случайные величины. Числовые характеристики дискретной случайной величины
- •Теорема сложения независимых событий
- •Случайные величины
- •Закон распределения дискретной случайной величины
- •Числовые характеристики случайной величины
- •Дисперсия дискретной случайной величины
- •Среднее квадратическое отклонение
- •Функция распределения случайной величины
- •График функции распределения
- •Плотность распределения вероятностей. Дифференциальная функция распределения
- •Свойства плотности распределения
- •Характеристики непрерывных случайных величин
- •Нормальное распределение
- •Влияние параметров нормального распределения на форму нормальной кривой
- •Вероятность попадания в заданный интервал нормальной случайной величины
- •Занятие 6.Статистическое распределение выборки, дискретные и интервальные вариационные ряды. Точечные оценки параметров распределения. Доверительный интервал и доверительная вероятность.
- •Генеральная и выборочная совокупности
- •Статистический дискретный ряд распределения
- •Статистический интервальный ряд распределения
- •Полигон и гистограмма
- •Эмпирическая функция распределения
- •Оценки характеристик распределения
- •Оценка математического ожидания
- •Оценка дисперсии
- •Оценка среднего квадратического отклонения
- •Интервальные оценки
- •2. Результаты наблюдений за числом частиц, попавших в счетчик Гейгера в течение минуты, приведены в виде интервального ряда распределения:
- •Построим гистограмму (рис. 9.4)
- •3. Найти оценку математического ожидания и несмещенную оценку дисперсии, если дана таблица распределения:
- •Решение. Для вычисления характеристик воспользуемся расчетной таблицей:
- •Самостоятельная работа студентов на занятии
- •Занятие 7.Погрешности измерений и их оценки. Погрешности прямых и косвенных измерений
- •Погрешности измерений. Истинная, абсолютная и относительные погрешности
- •Типы погрешностей
- •Оценка истинного значения измеряемой величины
- •Вычисление абсолютной погрешности косвенных измерений
- •Занятие 8.Контрольная работа
- •Занятие 9.Деловая игра «Статистика знает все»
- •Приложения
- •I. Греческий алфавит
- •II. Некоторые постоянные
- •III. Обратные величины, степени, корни, логарифмы
- •IV. Значение функции ех и е -х
- •V. Тригонометрия Значения тригонометрических функций
- •Критические значения распределения Стьюдента
- •Значения функции и
- •Библиографический список
- •Практикум по математике
Дифференциалы высших порядков
Пусть y=f(x)
дифференцируемая функция, а ее аргумент
х
– независимая переменная. Тогда ее
первый дифференциал
![]() есть
также функция х,
можно найти дифференциал этой функции.
есть
также функция х,
можно найти дифференциал этой функции.
Дифференциал
от дифференциала функции называется
ее вторым дифференциалом (или
дифференциалом второго порядка) и
обозначается
![]() :
:
![]() .
.
Дифференциал
второго порядка от данной функции равен
произведению второго порядка этой
функции на квадрат дифференциала
независимой переменной:
![]() .
.
Приложение дифференциального исчисления
Функция называется
возрастающей
(убывающей)
на интервале (a;
b),
если для любых двух точек x1
и x2
из указанного интервала, удовлетворяющих
неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() (
(![]() ).
).
Необходимое
условие возрастания (убывания):
Если дифференцируемая функция на
интервале (a,
b)
возрастает (убывает), то производная
этой функции неотрицательна
(неположительна) в этом интервале
![]() (
(![]() ).
).
Достаточное условие возрастания (убывания): Если производная дифференцируемой функции положительна (отрицательна) внутри некоторого интервала, то функция возрастает (убывает) на этом интервале.
Функция f(x) в точке х1 имеет максимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x1)>f(x), при xx1.
Функция f(x) в точке х1 имеет минимум, если для любого х из некоторой окрестности точки выполняется неравенство: f(x1)<f(x), при xx1.
Экстремум функции называют локальным экстремумом, так как понятие экстремума связано лишь с достаточно малой окрестностью точки х1. Так что на одном промежутке функция может иметь несколько экстремумов, причем может случиться, что минимум в одной точке больше максимума в другой. Наличие максимума или минимума в отдельной точке интервала не означает, что в этой точке функция f(x) принимает наибольшее или наименьшее значение на этом интервале.
Необходимое условие экстремума: В точке экстремума дифференцируемой функции ее производная равна нулю.
Достаточное условие экстремума: Если производная дифференцируемой функция в некоторой точке х0 равна нулю и меняет свой знак при переходе через это значение, то число f(х0) является экстремумом функции, причем если изменение знака происходит с плюса на минус, то максимум, если с минуса на плюс, то минимум.
Точки, в которых производная непрерывной функции равна нулю или не существует называются критическими.
Исследовать функцию на экстремум означает найти все ее экстремумы. Правило исследования функции на экстремум:
Найти критические точки функции у = f(x) и выбрать из них лишь те, которые являются внутренними точками области определения функции;
Исследовать знак производной f'(x) слева и справа от каждой из выбранных критических точек;
На основании достаточного условия экстремума выписать точки экстремума (если они есть) и вычислить значения функции в них.
Для того чтобы найти наибольшее и наименьшее значение функции на отрезке необходимо выполнить несколько этапов:
Найти критические токи функции, решив уравнение f’(x)=0.
Если критические точки попали на отрезок, то необходимо найти значения в критических точках и на границах интервала. Если критические точки не попали на отрезок (или их не существует), то находят значения функции только на границах отрезка.
Из полученных значений функции выбирают наибольшее и наименьшее и записывают ответ, например, в виде:
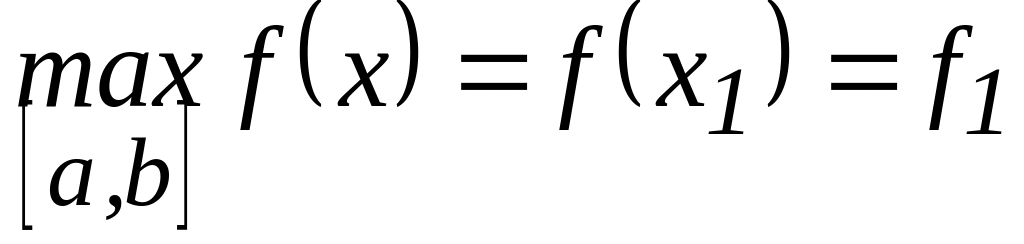 ;
;
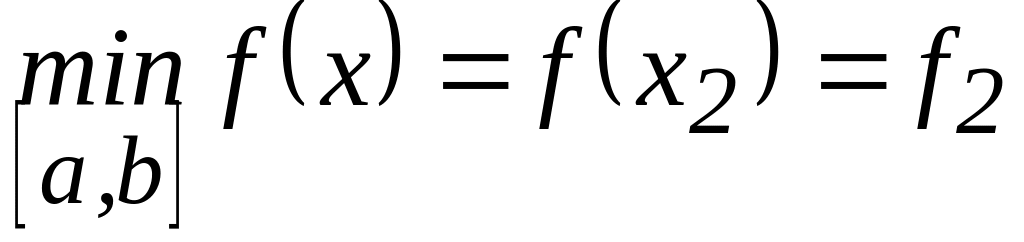 .
.
Решение задач
Пример
2.1. Найти дифференциал функции:![]() .
.
Решение. На основании свойства 2 дифференциала функции и определения дифференциала имеем:
![]() .
.
Пример
2.2. Найти дифференциал функции:
![]()
Решение. Функцию
можно записать в виде:
![]() ,
,
![]() .
Тогда имеем:
.
Тогда имеем:
![]()
Пример
2.3. Найти вторую производную функции:
![]()
Решение.
Преобразуем функцию
![]() .
.
Найдем первую
производную:
![]()
![]()
![]() ;
;
найдем вторую производную:
![]()
![]() .
.
Пример
2.4. Найти дифференциал второго порядка
от функции
![]() .
.
Решение.
Найдем дифференциал второго порядка
на основании выражения для вычисления
![]() :
:
![]() .
Найдем сначала первую производную:
.
Найдем сначала первую производную:
![]() ;
найдем вторую производную:
;
найдем вторую производную:
![]() .
.
Тогда
![]() .
.
Пример
2.5. Найти
угловой коэффициент касательной к
кривой
![]() ,
проведенной в точке с абсциссой х=2.
,
проведенной в точке с абсциссой х=2.
Решение.
На основании геометрического смысла
производной имеем, что угловой коэффициент
равен производной функции в точке,
абсцисса которой равна х.
Найдем
![]() .
.
Вычислим
![]() –
угловой коэффициент касательной к
графику функции.
–
угловой коэффициент касательной к
графику функции.
Пример
2.6. Популяция
бактерий в момент времени t
(t
измеряется
в часах) насчитывает
![]() особей. Найти скорость роста бактерий.
Найти скорость роста бактерий в момент
времени t
= 5 часов.
особей. Найти скорость роста бактерий.
Найти скорость роста бактерий в момент
времени t
= 5 часов.
Решение.
Скорость
роста популяции бактерий – это первая
производная
![]() по времени t:
по времени t:
![]() .
.
Если t
= 5 часов, то
![]() .
Следовательно, скорость роста бактерий
составит 1000 особей в час.
.
Следовательно, скорость роста бактерий
составит 1000 особей в час.
Пример
2.7.
Реакция организма на введенное лекарство
может выражаться в повышении кровяного
давления, уменьшении температуры тела,
изменении пульса или других физиологических
показателей. Степень реакции зависит
от назначенной дозы лекарства. Если х
обозначает дозу назначенного лекарства,
а степень реакции у
описывается функцией
![]() .
При каком значении х
реакция максимальна?
.
При каком значении х
реакция максимальна?
Решение.
Найдем производную
![]() .
.
Найдем
критические точки:
![]() ⇒
⇒
![]() .
⇒
Следовательно,
имеем две критические точки:
.
⇒
Следовательно,
имеем две критические точки:
![]() .
Значение
.
Значение
![]() не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Найдем
вторую производную
![]() .
Вычислим значение второй производной
при
.
Вычислим значение второй производной
при
![]() .
.
![]() .
Значит,
– уровень дозы, который дает максимальную
реакцию.
.
Значит,
– уровень дозы, который дает максимальную
реакцию.
Примеры для самостоятельного решения
Найти дифференциал функции:
 .
. .
. .
.
Найти вторые производные следующих функций:
 .
. .
. .
.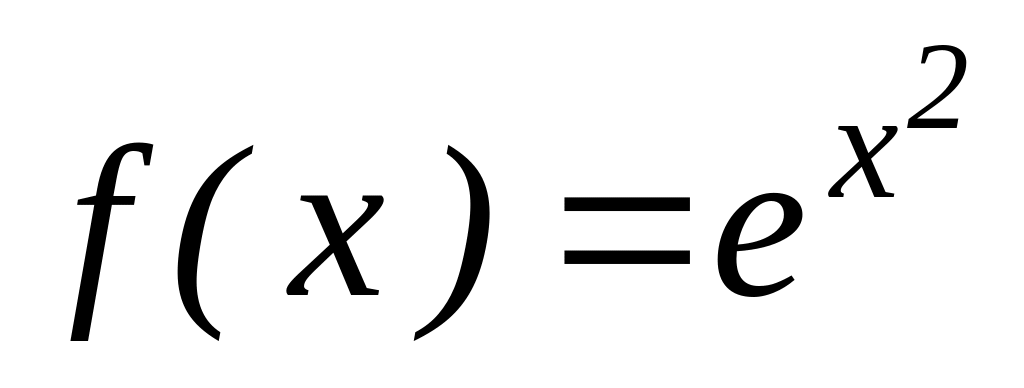 .
.
Найти производные второго порядка и записать дифференциалы второго порядка для следующих функции:
 .
. .
.Исследовать функцию на экстремум
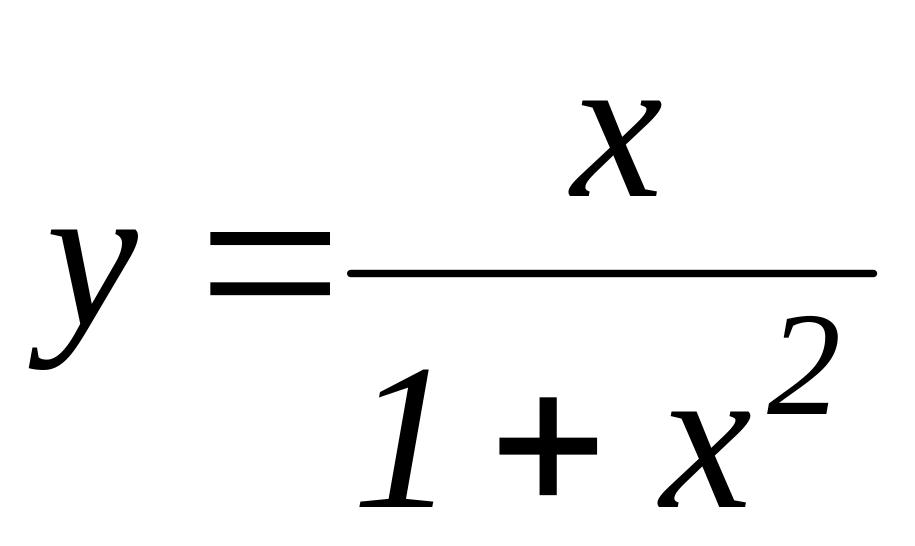 .
.Найти наибольшее и наименьшее значения функции
 на отрезке
на отрезке
 .
.Найти интервалы возрастания и убывания функции, точки максимума и минимума и точки пересечения с осями:

Закон движения точки имеет вид
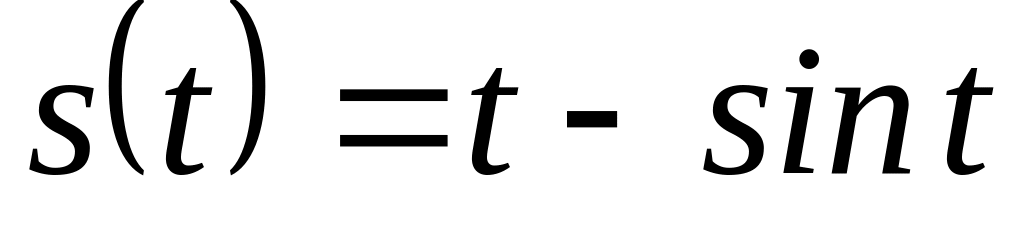 .
Определить закон скорость и ускорение
этой точки.
.
Определить закон скорость и ускорение
этой точки.Уравнение движения точки имеет вид
 (м). Найти 1) положение точки в моменты
времени
(м). Найти 1) положение точки в моменты
времени
 с и
с и
 с; 2) среднюю скорость за время, прошедшее
между этими моментами времени; 3)
мгновенные скорости в указанные моменты
времени; 4) среднее ускорение за указанный
промежуток времени; 5) мгновенные
ускорения в указанные моменты времени.
с; 2) среднюю скорость за время, прошедшее
между этими моментами времени; 3)
мгновенные скорости в указанные моменты
времени; 4) среднее ускорение за указанный
промежуток времени; 5) мгновенные
ускорения в указанные моменты времени.
Задание на дом.
Практика:
Найти дифференциал функции:
 ;
; ;
;
Найти производные второго порядка функции:
 .
.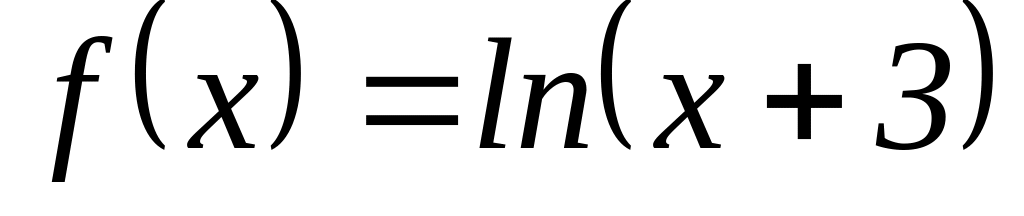

Найти дифференциалы второго порядка
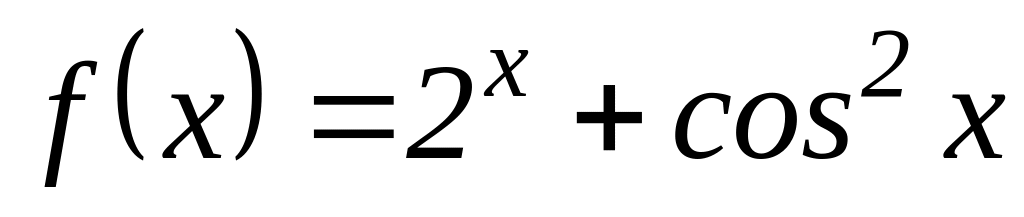 .
.
Точка движется прямолинейно по закону
 .
Вычислить скорость и ускорение в
моменты времени
.
Вычислить скорость и ускорение в
моменты времени
 и
и
 .
.
Найти интервалы возрастания и убывания функций:
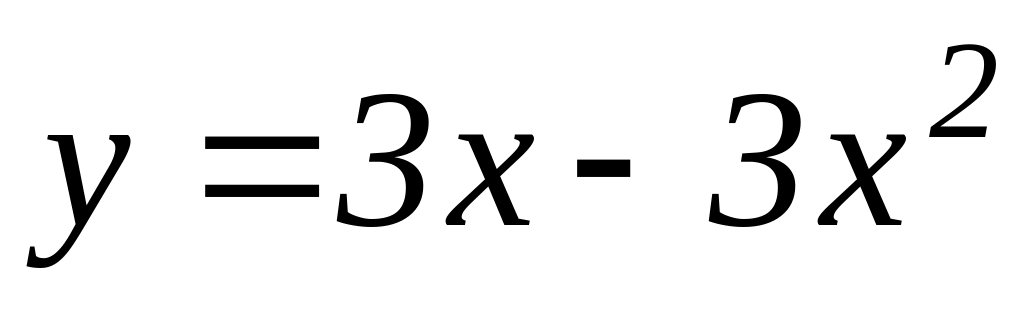 .
.
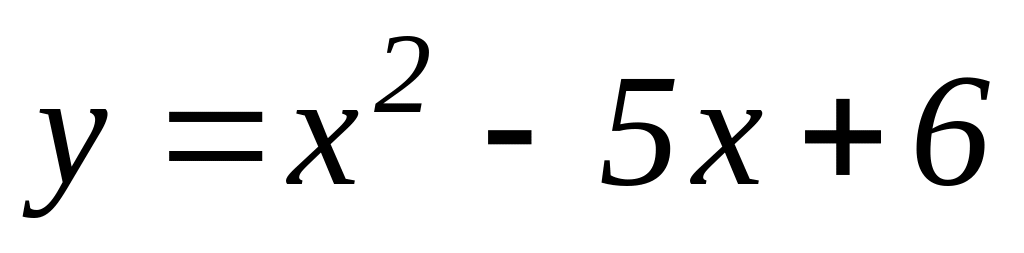 .
.При вливании глюкозы ее содержание в крови человека, выраженное в соответствующих единицах, спустя t часов составит
 .
Найдите скорость изменения содержания
глюкозы в крови при а) t
=1
ч; б) t
=2
ч.
.
Найдите скорость изменения содержания
глюкозы в крови при а) t
=1
ч; б) t
=2
ч.
Теория.
Лекция по теме «Производные и дифференциалы функции нескольких аргументов. Приложение дифференциала функции нескольких аргументов».
Занятие 3 данного методического пособия.
Павлушков И.В. и другие стр. 101-113, 118-121.
