2.5. Проведення регресійного аналізу засобами ms Excel.
2.5.1. Розрахунок параметрів лінійної регресії з використанням функції линейн.
Для лінійної апроксимації в Excel існує функція ЛИНЕЙН (від. зн. Y, від. зн. X, константа, статистика) вона повертає масив значень описуючих криву виду:
Де: від. зн. Y - це відомі значення функції від. зн. X - це відомі значення аргументів
константа – визначає чому має дорівнювати b, якщо константа має значення ХИБНО то b вважається рівним 1, інакше b обчислюється звичайним чином.
статистика – якщо значення дорівнює ІСТИННО то буде представлена додаткова регресійна статистика, якщо ХИБНО тоді ні.
Для отримання лінійної регресійної залежності, з виводом всієї статистичної інформації слід виділити діапазон A54: С58, натиснути клавішу F2, і ввести формулу = ЛИНЕЙН (P2: P38; N2: O38; 1; 1), після закінчення введення формули натиснути комбінацію клавіш Ctrl + Shift + Enter так як дана функція повертає масив значень. У результаті в даних осередках буде повна статистична інформація
Лінійна залежність |
||
0.645 |
0.176 |
229.123 |
0.039 |
0.038 |
94.969 |
0.963 |
115.657 |
#Н/Д |
441.156 |
34 |
#Н/Д |
11802358 |
454805 |
#Н/Д |
Отримані числа мають наступний зміст:
mn |
mn-1 |
… |
b |
Sen |
Sen-1 |
… |
Seb |
R2 |
Sey |
|
|
F |
Df |
|
|
Ssreg |
Ssresid |
|
|
Se – стандартна помилка для коефіцієнта m
Seb – стандартна помилка для вільного члена b
R2 – коефіцієнт детермінованості, який показує як близько рівняння описує вихідні дані. Чим ближче він до 1, тим більше сходиться теоретична залежність і експериментальні дані.
Sey – стандартна помилка для y
F - критерій Фішера визначає випадкова чи ні взаємозв'язок між залежною і незалежною змінними Df - ступінь свободи системи Ssreg - регресійна сума квадратів Ssresid - залишкова сума квадратів
Аналогічним чином побудуємо лінійну регресійну залежність при аргументі Константа рівному 0, в діапазоні E54: G58, ввівши формулу =ЛИНЕЙН(P2:P38;N2:O38;0;1):
Лінійна залежність |
||
0.728 |
0.146 |
0 |
0.021 |
0.039 |
#Н/Д |
0.9980 |
123.365 |
#Н/Д |
8925.124 |
35 |
#Н/Д |
2.7E+08 |
532666 |
#Н/Д |
2.5.2. Розрахунок параметрів лінійної регресії з використанням інструменту Регрессия надстройки Пакет анализа.
Для проведення регресійного аналізу виберемо пункт меню Сервис/Анализ данных/Регрессия. Відкриється наступне діалогове вікно:
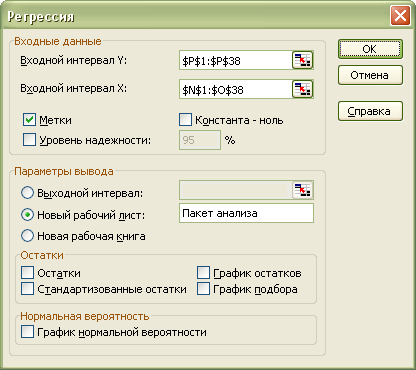
Після заповнення полів введення натискаємо кнопку OK і отримуємо наступні результати:
Регрессионная статистика |
|
Множественный R |
0.981 |
R-квадрат |
0.963 |
Нормированный R-квадрат |
0.961 |
Стандартная ошибка |
115.657 |
Наблюдения |
37 |
Дисперсионный анализ |
|
|
|
||
|
df |
SS |
MS |
F |
Значимость F |
Регрессия |
2 |
11802358 |
5901179 |
441.156 |
4.79E-25 |
Остаток |
34 |
454805.4 |
13376.63 |
|
|
Итого |
36 |
12257163 |
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t статистика |
P Значение |
Нижние 95% |
Верхние 95% |
Нижние 95.0% |
Верхние 95.0% |
Y |
229.123 |
94.969 |
2.413 |
0.021 |
36.122 |
422.123 |
36.122 |
422.123 |
X2 |
0.176 |
0.038 |
4.597 |
0.000 |
0.098 |
0.255 |
0.098 |
0.255 |
X5 |
0.645 |
0.039 |
16.336 |
1.15E-17 |
0.565 |
0.726 |
0.565 |
0.726 |
Результати, отримані при розрахунку з використанням інструменту Регрессия надстройки Пакет анализа, збіглися з результатами, отриманими за допомогою функції ЛИНЕЙН при аргументі Константа має значення ИСТИНА.