2.4. Регресійні моделі та способи їх розрахунку.

Нехай в результаті вимірювань в процесі досвіду отримана таблиця деякій залежності f(x):

			…		…
			…		…

Потрібно знайти формулу, яка має цю залежність аналітично.

Поставимо задачу так, щоб з самого початку враховувався характер вихідної функції. Знайти функцію заданого виду , яка в вузлових точках приймає як можна більш близькі значення до значень з таблиці

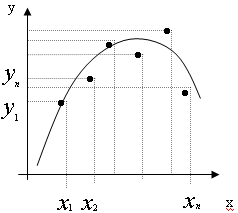
Практично вид наближає функції F встановлюють таким чином: по таблиці будується точковий графік функції f, а потім проводиться плавна крива, по можливості найкращим чином відображає характер розташування точок:

У вузлових точках функції f (x) і F (x) будуть відрізнятися на величину . (1) Відхилення можуть приймати «+» або «-» значення. Щоб ці знаки не враховувати, зведемо кожне відхилення в квадрат і підсумуємо квадрати відхилень по всіх вузлах:

. (2)

Метод побудови наближають функції F (x) з умови мінімуму величини Q називається методом найменших квадратів.

Як наближають функцію залежно від характеру точкового графіка функції f часто використовують такі функції:

1. ;	3. ;	5. ;	7. ;
2. ;	4. ;	6. ;	8. .

Тут - параметри. Коли вид наближає функції (1-8) встановлено, завдання зводиться тільки до відшукання параметрів. Розглянемо метод їх знаходження в загальному вигляді на прикладі F з трьома параметрами:

Нехай (3), де - постійні, - незалежна змінна, тоді значення та з виразу (2) набуде вигляду

= (4)

і є функцією трьох змінних (параметрів a, b, c). Завдання зводиться до відшукання її мінімуму.

Використовуємо необхідну умову екстремуму власної похідної функції повинна дорівнювати нулю: , тобто отримуємо систему з наступних рівнянь

(5)

Вирішивши цю систему трьох рівнянь з трьома невідомими щодо параметрів a, b, c, ми і отримаємо конкретний вид шуканої функції F (x, a, b, c).

Зміна кількості параметрів не змінить самого підходу, а призведе лише до зміни кількості рівнянь в системі (5).

Побудувавши функцію F (x), знаходять суму квадратів відхилень Q. З двох різних наближень вибирають те, для якого ця сума мінімальна. Зазвичай при обробці експериментальних даних, визначених з похибкою , узгодять похибка  з похибкою МНК, . Це дає оптимальний результат.

2.4.1. Лінійна функція (лінійна регресія).

Нехай наближаюча функція має вигляд: F (x, a, c) = ax + b

Тоді власні похідні:

Складемо систему виду (3): (1) (2)

Розділимо кожне рівняння системи (2) на n і приведемо її до наступного вигляду: .

Позначимо: (3)

Тоді система має вигляд: (4)

Коефіцієнти цієї системи - числа, які легко обчислюються в кожній конкретній задачі за формулами (3) через значення і з вихідної таблиці.

Вирішивши останню систему (4), отримуємо конкретний вид лінійної функції y = ax + b.