2.3. Проведення кореляційного аналізу засобами ms Excel.
Для побудови матриці коефіцієнтів парної кореляції необхідно вибирати команду меню Сервіс / Аналіз даних / Кореляція. Відкриється наступне діалогове вікно:
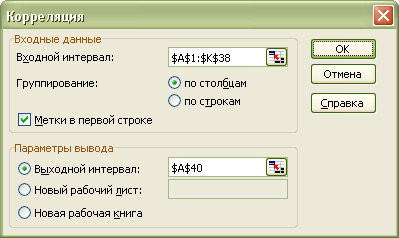
Далі слід натиснути кнопку OK. Після цього буде створена матриця коефіцієнтів парної кореляції:
|
Y |
X0 |
X1 |
X2 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
X10 |
Y |
1 |
|
|
|
|
|
|
|
|
|
|
X0 |
0.954 |
1 |
|
|
|
|
|
|
|
|
|
X1 |
0.926 |
0.880 |
1 |
|
|
|
|
|
|
|
|
X2 |
0.820 |
0.795 |
0.609 |
1 |
|
|
|
|
|
|
|
X4 |
0.917 |
0.835 |
0.926 |
0.716 |
1 |
|
|
|
|
|
|
X5 |
0.969 |
0.918 |
0.960 |
0.740 |
0.965 |
1 |
|
|
|
|
|
X6 |
0.817 |
0.739 |
0.660 |
0.888 |
0.747 |
0.751 |
1 |
|
|
|
|
X7 |
-0.920 |
-0.885 |
-0.891 |
-0.689 |
-0.928 |
-0.939 |
-0.680 |
1 |
|
|
|
X8 |
0.968 |
0.914 |
0.963 |
0.721 |
0.954 |
0.973 |
0.746 |
-0.953 |
1 |
|
|
X9 |
0.943 |
0.874 |
0.852 |
0.881 |
0.923 |
0.924 |
0.833 |
-0.885 |
0.921 |
1 |
|
X10 |
0.947 |
0.879 |
0.863 |
0.873 |
0.934 |
0.934 |
0.819 |
-0.898 |
0.930 |
0.998 |
1 |
Аналіз матриці коефіцієнтів парної кореляції показує, що істотний вплив на залежну змінну надають всі фактори. Для виключення явища мультиколінеарності всі фактори крім X2 і X5 слід виключити з моделі.