2.2. Основное уравнение гидростатики

Для вывода основного уравнения гидростатики, уста­навливающего зависимость давления р в точке от характера дей­ствующих в жидкости массовых сил, рассмотрим равновесие эле­ментарного прямоугольного параллелепипеда со сторонами dx, dy, dz, выделенного внутри покоящейся жидкости (рис. 2.2). Пусть на единицу массы параллелепипеда действует массовая сила её составляющими X, Y и Z. Если на три грани, пересе­кающиеся в точке О, будет действовать давление р, то на соот­ветствующих противоположных гранях (рис. 2.2) давления будут равны:

; .

Тогда уравнения равновесия в проекциях на оси х, y, z будут иметь вид

,

или

Три последних уравнения являются основными уравнениями гидростатики и называются уравнениями Эйлера равновесия жидкости или газа.

Эта система уравнений иногда записывается в виде:

(2.2)

Так как

,

и

,

то, очевидно, система уравнений (2.2) может быть представлена в векторном виде

(2.3)

Если систему (2.2) умножим последовательно на dx, dy, dz и сложим, то получим

Так как правая часть последнего уравнения есть полный дифференциал

, (2.4)

то уравнение (2.4) будет иметь вид

. (2.5)

Следовательно, при наличии равновесия полным дифферен­циалом должна быть и левая часть уравнения (2.4). В частности, при постоянной плотности ( = const) получим

Из этого уравнения видно, что массовые силы имеют потен­циал и проекции массовых сил можно выразить в виде:

(2.6)

Тогда уравнение (2.5) запишется таким образом:

Из этого следует, то жидкость может находиться в равно­весии только в том случае, когда массовые силы, действующие в ней, имеют потенциал, т. е. проекции массовых сил удовлетво­ряют условию (2.6).

Поверхность, в каждой точке которой давление постоянно, называют поверхностью уровня. Если в уравнении (2.5) положить р = const, то уравнение поверхности уровня будет

Х dx + У dy + Z dz = О,

или

dФ = 0.

Из последнего уравнения следует, что поверхность уровня одновременно является поверхностью равного потенциала или так называемой эквипотенциальной поверхностью.

2.3. Равновесие тяжелой несжимаемой жидкости

Для несжимаемой тяжелой жидкости при отсутствии других массовых сил, кроме сил тяжести, имеем (ось z направлена вертикально вниз) X=Y=0 и Z=g, уравнения равновесия (2.2) в этом случае принимают вид:

,

Первые два из этих уравнений выражают независимость да­вления от координат х и у, т. е. поверхностями равного давления или поверхностями уровня являются горизонтальные плоскости. Интегрирование третьего уравнения

(2.7)

при постоянных значениях g и  приводит к результату

. (2.8)

Если начало координат поместить на свободную поверхность покоящейся жидкости, на которой постоянное давление р₀ задано или для открытого сосуда равно атмосферному давлению, то, как следует из выражения (2.8), при z= 0, С = р_о. Подставив значение постоянной С в уравнение (2.8) и имея в виду, что pg =  ( - удельный вес жидкости), окончательно получим величину гидростатического давления в виде

(2.9)

Это соотношение является выражением общего гидростатиче­ского закона, который формулируется следующим образом:

давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с весом столба жидкости высотой от по­верхности до данной точки и с площадью основания, равной единице.

Заметим, что закон в такой редакции верен как для несжимае­мой, так и для сжимаемой жидкостей, т.е. для всех жидкостей и газов и их смесей. ^:

Размерность всех слагаемых в уравнении (2.9) будет иметь размерность давления — Н/м².

Закономерности, определяемые уравнением (2.9), широко ис­пользуются в различных гидростатических машинах и приборах.

К таким машинам можно отнести гидравлический пресс, гидравли­ческий аккумулятор, различные системы объемных передач и пр.

Большая часть гидростатических машин и приборов исполь­зует свойства сообщающихся сосудов. Общее свойство сообща­ющихся сосудов заключается в том, что если на свободных поверх­ностях сообщающихся сосудов давление одинаково и они запол­нены одинаковой жидкостью, то во всех сосудах уровни будут одинаковыми.

М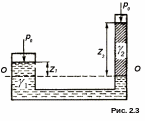 ожно показать, что в сообщающихся сосудах, заполненных жидкостями с различными удельными весами, высота столбов жидкостей над уровнем раздела обратно пропорциональна удель­ным весам. Из рис. 2.3 видно, что давления в обоих сообщающихся сосудах будут одинаковы на плоскости, проведенной через по­верхность раздела 00.

Приравняв давление в этом сечении в пра­вом и левом сосудах

получим, что .

Задача. В U образную трубу (рис. 2.4.) налиты вода и бензин. Определить плотность бензина, если Н_б=500мм, h_в=350мм. Капиллярный эффект не учитывать.

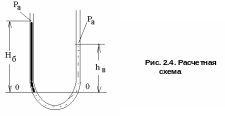
По основному уравнению гидростатики – давление по сечению 0-0 одинаково как для левой, так и для правой трубы.

р_а +_бgH_б = _вgh_в+p_a

где p_а – атмосферное давление, для левой и правой труб одинаково;

_в =1000кг/м³ - плотность воды.

Отсюда

_бgH_б = _вgh_в