3.7. Уравнение Бернулли

В потоке жидкости, движущейся в трубке с плавно изменяю­щимся сечением (см. рис. 3.4), выберем два произвольных сече­ния / и //. Обозначим р₁ и p₂ давления в центрах тяжести сечений ₁ и ₂, v₁ и v₂ - средние скорости, а z₁ и z₂—вертикальные координаты оси потока в выбранных сечениях.

Тогда величины полной удельной энергии потока в сечениях / и // соответственно могут быть записаны:

;

.

П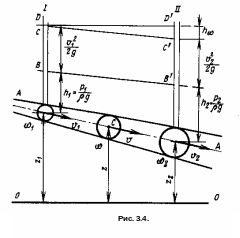 ри движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения до второго. Эта энергия обращается в тепло и рассеивается. Величину указанных потерь энергии обозна­чим h_. Тогда баланс энергии в сечениях / и // можно записать так:

.

Это уравнение называется уравнением Бернулли для реально­го потока жидкости. Оно устанавливает математическую связь между основными элементами движения жидкости, т. е. средней скоростью и гидродинамическим давлением. Оно показывает, что за счет преобразования одного вида энергии в другой наблюдает­ся при возрастании скорости уменьшение давления и, наоборот, при уменьшении скорости — возрастание давления.

Физический (энергетический) смысл уравнения Бернулли со­стоит в том, что при установившемся движении жидкости сум­ма трех удельных энергий (положения, давления и кинетической) остается неизменной.

Легко убедиться, что каждый член уравнения Бернулли име­ет размерность длины и показывает:

- высоту скоростного напора; пьезометрическую высоту, отсчитываемую в каждом сечении по пьезометру (см. рис. 3.4); z — геометрическую высоту; h_ — потерянный напор, равный части энергии, превращенной в тепло.

Сумма трех высот — скоростного напора, пьезометрической и геометрической — называется гидродинамическим напором:

.

3.8. Графическое представление и практическое применение уравнения Бернулли

Диаграмма уравнения Бернулли для потока реальной жидко­сти показана на рис. 3.4. От центров тяжести сечений / и // от­ложены отрезки, соответственно равные пьезометрическим высотам и , затем от точек В и В¹ отложены вверх отрезки, соответствующие высотам скоростного напора в этих сечениях

Линия О—О - след плоскости сравнения; линия ВВ' назы­вается пьезометрической линией; линия СС' — напорной линией; линия DD' — линией первоначального напора. Очевидно, отре­зок D'C' соответствует потере напора h_ по длине потока на участке между сечениями / — //.

На основании уравнения Бернулли сконструирован ряд при­боров, такие, как , водоструйный насос, эжектор и др.

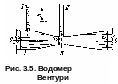Рассмотрим применение уравнения Бернулли на примере водомерного устройства в трубах — водомера Вентури (рис. 3.5), представляющего собой вставку в основную трубу диамет­ром D трубы меньшего диаметра d, которая соединена с основной трубой коническими переходами. В основной трубе (сечение 1—1) и в суженном сечении (сечение //—//) присоединены пьезометры, по показаниям которых и определим расход жидко­сти Q в трубе.

Выведем общую формулу водомера для определения расхода жидкости.

Предварительно приняв для заданных условий z₁=z₂=0, ₁=1 и ₂=1 и h_=0 (ввиду малости расстояния между се­чениями), можем записать уравнения Бернулли в виде:

.

Отсюда следует, что с увеличением скорости движения пьезометрическое давление уменьшается и наоборот. Это положение используется в водомере Вентури, где по разности показаний пьезометров h, зная диаметры D и d, можно определить мгновенный поток.

где и - площади соответствующих сечений

В 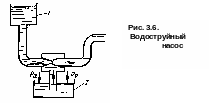водоструйном насосе (рис. 3.6) вода из бака 1 поступает в трубу, имеющую сужение. В узком сечении трубы скорость струи возрастает. При этом в соответствии с уравнением Бернулли давление здесь падает ниже атмосферного, благодаря чему происходит подсасывание жидкости по трубке, опущенной в бак 2. При больших скоростях движения жидкость будет подса­сываться из бака 2 непрерывно.

Скорость течения движущейся жидкости можно определить трубкой Пито. Этот прибор (рис. 3.7) представляет собой стек­лянную трубку, открытую с двух концов. При этом изогнутый под прямым углом конец трубки располагается в жидкости так, чтобы ось нижнего колена совпадала с линией тока. В трубке Пито создается дополнительное давление от воз­действия скорости движущейся жидкости (скоростной напор).

Измерение скорости в потоке закрытого трубопровода можно провести по разности показаний трубки Пито , определяющей полный напор h₁=((p/g)+v²/(2g)), и пьезометрической трубки, определяющей пьезометрический напор – h₂=p/g. Скорость потока (м/с) в точке расположения нижнего отверстия трубки Пито можно определить по высоте подъема жидкости h₃= v²/(2g).

П рименяя уравнение Бернулли к случаю истечения жидкости через малое отверстие при постоянном напоре, получаем выражение для расхода жидкости, известное как формула Торричелли:

где  — коэффициент расхода (истечения), который определяется экспериментально и зависит от вида (формы) отверстия; f — площадь поперечного сечения отверстия; h — напор.

Учитывая, что напор h=p/(g), формулу Торичелли преобразуем к виду

где Δp — перепад давления в отверстии.

Эту формулу часто используют для расчета процессов дросселирования, прохождения жидкости через местное гидравлическое сопротивление (золотники, клапаны и другие гидроаппараты).