2.9. Равновесие и остойчивость тел, погруженных в жидкость

2.9.1. Закон Архимеда

Рассмотрим силы давления жидкости на тело, погруженное в эту жидкость (рис. 2.15, а).

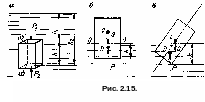
Тело призматической формы имеет высоту h и площадь верхнего и нижнего оснований . Верхнее основание погружено в жидкость на глубину h₁, нижнее — на глубину h₂. При этом на тело действуют:

сила гидростатического давления жидкости на верхнее осно­вание

сила гидростатического давления жидкости на нижнее осно­вание

силы давления жидкости на боковые поверхности (грани призмы) не учитываются, так как они взаимно уравновешены.

Равнодействующая сил гидростатического давления равна разности сил P₁ и P₂ и направлена вверх (в сторону большей) силы):

,

или

Таким образом, на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом. Это и есть закон Архимеда, открытый им в 250 г. до н. э.

Закон Архимеда справедлив для тел любой фирмы, так как тело другой, отличающейся от призматической и более сложной формы можно представить состоящим из бесконечного множе­ства элементарных вертикальных призм.

2.9.2. Равновесие тел погруженных в жидкость

На тело, погруженное полностью или частично в жидкость, действуют две силы:

• Сила тяжести тела G, приложенная в его центре тяжести С, действует сверху вниз;

• Выталкивающая сила Р, приложенная в центре давления или, как называют еще, в центре водоизмещения D, которая направлена снизу вверх (рис.2.15, б).

Центром водоизмещения является центр тяжести вытесненного объема жидкости. В зависимости от соотношения сил G и Р могут быть три состояния тела, погруженного в жидкость:

• Если G больше Р, тело тонет;

• Если G=Р, тело находится внутри жидкости в безразличном состоянии (тело плавает в погруженном состоянии);

• Если G меньше Р, тело всплывает до тех пор, пока сила тяжести вытес­ненной жидкости (т. е. выталкивающая или подъемная сила Р) не станет равна силе тяжести тела G.

Для равновесия тела, плавающего на свободной поверхности, необходимо, чтобы центр тяжести и центр давления (водоиз­мещения) лежали на одной вертикали. В самом деле, из рис.2.15, в ясно, что в случае когда центр тяжести тела и центр давления не лежат на одной вертикали (например, при наклоне или, как говорят, крене тела), появляется пара сил Р и G, которая стре­мится вращать тело.

Введем некоторые понятия. Линия пересечения свободной поверхности жидкости с поверхностью плавающего тела называется ватерлинией. Глубина погружения самой низкой точки под уровень свободной поверхности называется глубиной погружения, или осадкой.

Объем жидкости, вытесненной телом, называют объемным водоизмещением, а сила тяжести этого объема — весовым водоизме­щением (которое равно выталкивающей силе Р).

Задача. Прямоугольный понтон площадью 20*30 метров (рис.2.16) плавает в воде. Определить осадку h, если собственный вес понтона с грузом на нем G=12*10³ кН.

Решение. По условию плавучести весовое водоизмещение Р равно G, т.е. Р=G= 12*10³ кН.

Тогда по формуле , где V – объем погруженной части понтона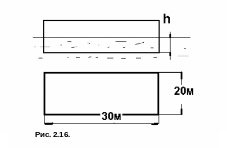

V=20*30*h, м³;

Учитывая плотность воды и силу тяжести можно записать

12*10³=10*20*30*h,

откуда осадка понтона

h=12*10³/(10*20*30) =2 м