Часть I.

Снятие вольтамперных характеристик источников энергии

и резистора

1 . Вольтамперные характеристики регулируемого и нерегулируемого источников энергии снимаются по схеме рис.1а. В качестве сопротивления нагрузки используется перемен-ный резистор стенда R₄ = 1000 Ом. При этом ток нагрузки не должен превышать 0.5 А.

Изменяя ток резисто-ром Rнг, снять несколько значений выходного напряжения источника Uвых. Данные измерений внести в таблицу 1.

2. Характеристика резистора снимается по схеме рис.1б. Здесь исполь-зуется регулируемый источник напряжения. Напряжение следует изменять в пределах 0 - Uдоп резистора. Результаты измерений внести также в таблицу 1.

Таблица 1.

Нерегулируемый			Регулируемый источн.			Резистор
Uвых	I,mA	Парам	Uвых	I,mA	Парам	UR,B	I,mA	R,Ом	Парам
		E1 = r01 =			E2 = r02 =				Rном = Рдоп = Iдоп =

3. По данным табл.1 построить графики характеристик резистора и источников энергии, определить их параметры.

Часть II

Исследование сложной цепи постоянного тока

4. При подготовке к работе необходимо просмотреть теоретический материал, относящийся к методам МН, МУП, МЭГ. Для своего варианта исследуемой схемы цепи одним из методов рассчитать токи.

5. Собрать схему исследуемой цепи своего варианта. Поочерёдно включая источники Е₁ и Е₂, измерить составляющие токов в ветвях.

Результаты измерений внести в табл. 2 для сравнения с расчётами.

6. При обоих включённых источниках измерить токи и потенциалы узлов. Результаты также внести в таблицу 2.

Таблица 2.

Результаты расчётов и измерений токов и узловых потенциалов

Режимы цепи		I1,мА	I2,мА	I3,мА	I4,мА	I5,мА
От ист.Е1=	Расчёт
	Эксперимент
От ист.Е2=	Расчёт
	Эксперимент
Включены оба источника	Расчёт
	Эксперимент

Результаты измерения потенциалов узлов в цепи.

Исследуемые величины	jА, В	jВ, В	jС, В
Расчёт
Эксперимент

7. Проверка метода эквивалентного генератора на примере тока I₄.

Для этого при включённых источниках э.д.с. Е₁ и Е₂, сначала разом-кнуть ветвь с сопротивлением r4 и измерить напряжение U₄х = Еэкв, а затем замкнуть ветвь накоротко, т.е. включить в неё только амперметр, и измерить ток I₄кз. По результатам измерений рассчитать соп-ротивление Rвх = Rэкв генератора, а также ток I₄ в рабочем режиме.

Rвх = Rэкв = ; I₄ = ;

Данные внести в таблицу 3. Таблица 3.

Результаты измерений и расчёта тока I4 по МЭГ.

Исследуемые величины	U4x, B	I4кз, mA	Rэкв, Ом	I4, mA
Расчёт
Эксперимент

8. При оформлении отчёта по работе выполнить аналитический рас-чёт тока I₄ по методу эквивалентного генератора. Результаты расчёта для сравнения также внести в табл. 3. Сделать выводы по работе.

------------------------- ♦ ---------------------------

*Пример расчёта тока I4 по методу эквивалентного генератора

Допустим, что в схеме на стр.3 э.д.с. источников: Е₁ = 20.3В, Е₂= 19В,

сопротивления: R₁ = 200 Ом, R₂ = 700 Ом, R₃ = 800 Ом,

R₄ = 75 Ом, R₅ = 300 Ом.

1.Определение э.д.с. эквивалентного генератора /см. схему цепи на стр.3 /

Токи I3x , I5x находим в оставшейся части цепи после размыкания ветви с резистором r₄.

Таким образом: Е экв = U4x = 300^. 0,0406 – 800^. 0,01267 = 2,05 B.

2. Определение сопротивления эквивалентного генератора Rэкв

493,33 Ом.

3.Теперь в схеме с эквивалентным генератором по закону Ома находим:

В таблицу 3, для сравнения, считаем также ток короткого замыкания на зажимах А-В ветви:

------------------ ---------------------

Построение потенциальной диаграммы для внешнего контура цепи

Для этого рисуем схему контура и наносим все его характерные точ-ки. Токи расставляем таким образом, чтобы они были положительны. Потенциалы точек контура можно рассчитывать относительно любой точки.

П усть jс = 0.

Тогда: ja = jс – R₂^. I₂ =

= 0 - 700^. 0,01072 = -7,504 B

j_A = ja + E₂ = + 11,5 B

j_B = j_A + R₄^.I₄ = 11,76B

jb = j_B – E₁ = - 8,54 B

jс = jb + R₁^. I₁ = 0.

По полученным значениям, в масштабах строим саму потенциальную диаграмму. При этом величины сопротивлений по оси абсцисс откла-дываются нарастающим итогом.

------------------------ ♦ -----------------------

Вопросы и задачи для самопроверки

1. Уберите из исследуемой схемы цепи резистор R3, после чего методом наложения определите ток первой ветви.

2. Изложите теорему об эквивалентных источниках. Как в лаборатории определяются их параметры?

3. В экспериментах получено: Uхх = 3.2 В, Iкз = 0.8А. Составьте схемы эквивалентных источников э.д.с. и тока, постройте вольтамперную характеристику исследуемого реального источника энергии.

4. На холостом ходу батарейка 1.7В, при токе 0.2 А напряжение падает до 1.3 В. Определите параметры батарейки и укажите, какую наи-большую мощность она может отдать в нагрузку.

5. Как экспериментально определяют входное сопротивление отно-сительно любой пары зажимов в цепи с неизвестными параметрами?

6.В исследованной цепи замените резистор R3 источником э.д.с. Е₃ = 24 В. Составьте уравнения для расчёта токов по МЗК и по МУП.

7. В исследованной цепи замените резистор R3 источником тока Jк = 0,125 А. Составьте уравнения для расчёта токов по МЗК и по МКТ.

8 .В исследуемой сложной цепи методом эквивалентного генерато-ра определите ток I1 или I2.

9. Исследованный в работе источник Е₁, r₀₁ замените эквивалентным источником тока, изобразите его схему.

10. Почему невозможна взаимная замена идеальных источников э.д.с. и тока?

------------------------ ♦ -----------------------

Лаборатория 311.

ЛАБОРАТОРНАЯ РАБОТА № 3-4

Определение параметров элементов и

исследование простейших цепей синусоидального тока

Цель работы:

- экспериментально определить параметры (сопротивления и проводимости) катушки и RС-двухполюсника;

- проверить расчётные соотношения ( Z, У, I, U, Р) при последовательном и параллельном соединении элементов.

Пояснения к работе

В цепях синусоидального переменного тока различают активное R, реактивные Х_L, Х_С и полные (импедансные) Z -сопротивления элементов. При параллельном соединении для расчёта цепи необходимы проводимости: g, b_L, b_C и у. Обычно эти параметры определяют экспериментально, с помощью вольтметра, амперметра и ваттметра.

При отсутствии ваттметра сопротивления определяют следующим образом: подключив элемент к источнику постоянного тока, находят его активное r -сопро-тивление, а затем, включив элемент на переменный ток, находят его полное z-со-противление. Проводимости двухполюсника при отсутствии ваттметра определя-ют расчётом через найденные сопротивления. Полную проводимость у двухполюс-ника можно проверить по результатам измерений.

r = , так как х_L⁽⁰⁾ = 0, Z = , Х = ; [1аб]

у = , g = = = r ∙ у ²; b = х∙ у ² = .

Расчёты простых цепей по закону Ома или по законам Кирхгофа ведутся в действующих или амплитудных значениях и через полные Z - сопротивления или у -проводимости.

Zвх = ; ║Увх = ; Zвх = ;

I = ; Uкат = Zкат ∙ I; ║ I = у_вх∙U; Iа = gвх ∙U; Iр = bвх ∙U;

Uвх= ║ Iвх = ;

φ = arctg ; ║ φ = arctg ; [2аб]

Р = U∙I∙cosφ = R ∙ I ² ; ║ Р = U∙I∙cosφ = g ∙ U ² , Вт.

Питание исследуемых элементов и цепей в лаборатории осуществляется от 3-фазного источника синусоидального тока частотой 50 Гц.

В лабораторной работе исследуются катушки К₁, К₂, К₃ и два RС-двух-полюсника.

Ориентировочные параметры исследуемых двухполюсников

Исследуемый двухполюсник	К-1	К-2	К-3	RС-1	RС-2
№ элемента на стенде	L1*	L2*	L4	С3	С2+С3
r, Ом	3,75	22	52	150	50
L, мГн	175	690	100	---	---
С, мкф	---	---	---	20	10+20

Таблица вариантов

Номер варианта	1	2	3	4	5	6
Первая ветвь схемы	К-1	К-2	К-3	К-1	К-2	К-3
Вторая ветвь схемы	RС-1	RС-1	RС-1	RС-2	RС-2	RС-2

Домашняя подготовка к работе

1. Записать название и цель лабораторной работы, ознакомиться с пояснениями к работе. В случае необходимости выписать основные расчётные формулы и вспомнить порядок построения ВД при последовательном и параллельном соединении элементов. Согласно Ваше-му варианту выбрать исследуемые двухполюсники, нарисовать их схе-мы и выписать ориентировочные параметры.

2. Нарисовать схему параллельного соединения двухполюсников и подготовить таблицу 2. При Uвх = 18 В выполнить расчёт величин для заполнения таблицы.

3. Нарисовать схему последовательного соединения двухполюсников и подготовить таблицу 3. Выполнить расчёт величин для заполнения таблицы.

4. Записать краткую последовательность выполнения работы в лаборатории.

Порядок выполнения работы

Определение сопротивлений и проводимостей двухполюсников

1. В соответствии с вариантом выбрать катушку и сформировать из элементов стенда RС-двухполюсник.

2. Подключить катушку к регулируемому источнику постоянного то -ка и, плавно повышая напряжение, при токе 100 ÷150 мА определить r -сопротивление. В случае RС-двухполюсника к источнику постоянного тока следует подключать только резистор R двухполюсника.

Для определения остальных параметров двухполюсник подключить к источнику синусоидального напряжения U~ 18 В частотой 50 Гц. На стенде это одна из фаз 3х-фазного источника.

По формулам [ 1аб ] рассчитать параметры элементов. Результаты измерений и расчётов внести в табл.1.

Таблица 1

Сопротивления и проводимости исследуемых двухполюсников

Исследуемый двухполюсник	U0,В	I0 , мА	U~ В	I~ мА	Сопротивления Ом			Проводимости, См∙10 - 2
					z	r	x	у	g	b
Катушка	1.72	358	18.1	296.5	61.0	4.8	60.85	1.638	0.13	1.633
RС-двухполюсн.	7.8	156	18.1	154.2	117.4	50	106.2	0.852	0.363	0.771

3. По результатам исследования записать сопротивления и проводимости двухполюсников в комплексной форме:

Z = r + j х Ом, У = g +jb См.

Проверка соотношений при параллельном соединении элементов

Напряжение Uвх = 18 В.

4. Собрать схему цепи с параллельным соединением двухполюсников. Включив оба двухполюсника одновременно, произвести измерения ве-личин, указанных в табл.2. Токи ветвей Iкат, I_RC принять из таблицы 1.

Таблица 2

Параллельное соединение двухполюсников

Исследуемые величины	Расчёт	Эксперимент
1. Входная проводимость цепи Увх, См	0.01705
2. Входное сопротивление цепи Zвх, Ом	58,66
3. Входное напряжение Uвх, В	18.1
4. Напряжение на резисторе RС -двухполюсн.	7.71
5. Напряжение на конденсаторе RС-двухполюс.	16.38
6. Входной (общий) ток I , мА	308.57
7. Ток в ветви катушки I кат , мА	296.5
8. Ток в RС-двухполюснике I RC , мА	153.2
9. Активная мощность цепи Рw, Вт	1.61	----

Сравнив результаты расчётов и измерений, сделать предварительные выводы о выполнении расчётных соотношений параллельного соединения двухполюсников.

Проверка соотношений последовательного соединения

двухполюсников. Напряжение Uвх = 36 В.

5. Собрать схему цепи с последовательным соединением двухпо-люсников и произвести измерения величин для табл.3.

Таблица 3

Последовательное соединение двухполюсников

Исследуемые параметры	Расчёт	Эксперимент
1.Входное сопротивление цепи Zвх, Ом	71.13
2.Входное напряжение Uвх, В	36
3.Ток I , мА	506
4.Напряжение на катушке Uкат, В	30.89
5.Напряжение на RС-двухполюснике URC, В	59.4
6.Напряжение на резисторе RС-двухполюсн.	25.3
7.Напряжение на конденсаторе RС-двухполю.	53.75
8.Активная мощность цепи Рw, Вт	14.04	-----

Сравнив результаты расчётов и измерений, сделать предварительные выводы о выполнении расчётных соотношений при последовательном соединении двухполюсников.

6. При оформлении отчёта расчётные величины в таблицах 2 и 3, полученные в домашней подготовке, необходимо уточнить в соответ-ствии с экспериментально полученными значениями сопротивлений r, x, z и проводимостей g, b, у (табл.1).

По данным таблиц 2 и 3 построить полные векторные диаграммы обеих цепей и сделать выводы по работе.

------------------------- ♦ -------------------------

Вопросы и задачи по лаб. работе № 3-4 для самопроверки

1.Каков физический смысл активного сопротивления и чем оно отличается от омического сопротивления, зависит ли от частоты?

2.Что такое индуктивность, что такое ёмкость, как рассчитывается их сопротивление синусоидальному переменному току? Постройте графики их со-противлений в функции частоты.

---------------------------- ● -----------------------------

3. Последовательно соединены двухполюсники Z₁, Z₂. Запишите в общем виде входное сопротивление Zвх цепи.

4. Последовательно соединены конденсатор С = 79,61 мкФ и катушка с параметрами: Rкат = 30 Ом, Lкат = 127,3 мГн. Определите входное сопроти-вление цепи на частоте 50 Гц. При токе I = 2 А найдите напряжения на ка-тушке и на конденсаторе. Постройте ВД цепи.

5. Последовательно включены реостат R и конденсатор: Хс = 80Ом, Uc = =120В, Рw =135 Вт. Определите величины сопротивления R, ёмкости С, тока, напряжения на входе цепи, построите векторную диаграмму.

---------------------------- ● -----------------------------

6. На напряжение 12 В параллельно включены конденсатор ХС = 8 Ом и реостат R = 2 Ом. Определите общий ток цепи по закону Ома и проверьте по I закону Кирхгофа. Постройте ВД цепи.

7. Параллельно включены реостат R = 12 Ом и конденсатор Хс= 6 Ом. Входной ток 3,354 А. Определите входное напряжение и токи ветвей.

8. В сеть Uвх =120 В последовательно включены реостат R =70 Ом и катушка: rкат =10 Ом, хкат = 60 Ом. Определить активную мощность и коэффициент мощности цепи, построить векторную диаграмму.

9. В сеть Uвх =36 В параллельно включены RL и RC- двухполюсники из второго эксперимента работы. Определите напряжение между средними точками ветвей.

10. Конденсатор С = 79,61 мкФ и катушка с параметрами: Rкат = 30 Ом, Lкат = 127,3 мГн соединены параллельно. Определите входное сопротивление цепи на частотах 50 и 100 Гц. 10а. Замените цепь эквивалентной последовательной. -------

Лаборатория 211.

РАСЧЁТНО-ЛАБОРАТОРНАЯ работА № 5

«Резонансные явления в цепях синусоидального тока.

Характеристики последовательного и параллельного

колебательных контуров»

Цель работы: -экспериментально проверить условия и признаки воз-никновения резонанса напряжений и резонанса токов;

- получить основные характеристики последовательного и параллельного резонансных контуров.

Пояснения к работе

Известно, что реактивные L и С - элементы дуальны, их сопротивления Х_L = ωL и Х_С = 1/ωС зависят от частоты и, в силу своей природы, действуют так, что могут компенсировать друг друга.

*Резонансными режимами называют режимы работы пассивных цепей, со-держащих индуктивности и ёмкости, при которых входное сопротивление или входная проводимость цепи имеют чисто активный характер, а входной ток и напряжение совпадают по фазе. При этом сами цепи называют резонан-сными или колебательными контурами.

*Колебательные контуры принято характеризовать: волновым сопротивлением ρ, резонансной частотой ω₀, добротностью Q, полосой пропускания Δ = ω₁ - ω₂, которую называют избирательностью контура, и расстройкой контура δ₁ = ω₀ - ω₁ или δ₂ = ω₂ - ω₀. Но исчерпывающе полной характеристикой контура являются его частотные характеристики Х_L(ω), Х_С(ω), Z(ω) и резонансные кривые I(ω), U_L(ω), U_C(ω).

* Различают режимы резонанса напряжений и резонанса токов.

ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

РЕЗОНАНС НАПРЯЖЕНИЙ

Резонансный режим может быть достигнут изменением индуктивности L, ёмкости С или частоты ω. В работе этот режим обеспечивается изменением индуктивности L катушки.

← Рис.1.

* Условия резонанса и резонансная частота контура:

Х_L= Х_С, ωL = 1/ωС, Х = Х_L-Х_С = 0 ω₀ = [1,2]

* Волновое или характеристическое сопротивление контура - это его ре-активное сопротивление в момент резонанса:

Х₀ = ω₀L = 1/ω₀С = = ρ; [3]

В момент резонанса напряжений общее реактивное сопротивление контура равно нулю: Х = Х_L- Х_С = 0, входное сопротивление цепи будет наименьшим: Zвх = R. Ток будет наибольшим, cos φ = 1, и активная мощность цепи Рw = U∙ I = S.

Таким образом, о наступлении резонанса напряжений можно судить по наибольшему току в цепи, а уточнять - по показанию ваттметра, сравнивая его с произведением показаний амперметра и вольтметра.

* В момент резонанса, в случае, если Х_L = Х_С > R, напряжения на индуктив-ности и на ёмкости могут значительно превышать напряжение источника:

U_L0 = U_С0 = Х₀∙ I = ρ∙ I > Uвх = Zвх∙ I = R∙ I .

Отношение напряжений на реактивных элементах при резонансе к напряжению источника называют добротностью контура Q. Добротность контура Q можно рассматривать и просто как соотношение параметров контура.

Q = = = ; [4]

* Полоса пропускания контура определяется по кривой тока I(ω), на уров-не 0.707 Iмакс, так как именно при таком снижении тока мощность (энергия) в реактивных элементах контура уменьшается вдвое. Типовой вид резонансных кривых последовательного кон-тура и выражения его частотных характеристик приведены на рис.2.

I(ω) = ;

U_L (ω) = Х_L(ω)∙I(ω);

U_С (ω) = Х_С(ω)∙I(ω).

Рис.2. Резонансные кривые последовательного контура

Заметим, что на резонансной частоте напряжения U_L и U_С равны, но их максимумы имеют место при частотах отличных от резонансной.

ω_С =ω₀ ∙ < ω₀, ω_L = ω₀ ∙ > ω₀. [5]

Необходимо также отметить, что все приведенные характеристики зависят от соотношения R, L, С-параметров контура, т.е. от добротности Q, которая может достигать значений Q макс = 100 -250.

Чем больше добротность контура, тем ос-трее резонансные кривые контура, тем лучше «настройка» контура на определённую частоту. При добротность Q ≤ 1 все кривые становятся весьма пологими.

В лабораторной работе при исследовании характеристик последовательного контура выполняются два эксперимента: при I макс = 2,5 А и при I макс = 1,4 А.

Рис.3. Резонансная кривая тока I(ω)

при различной добротности контура.

ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

РЕЗОНАНС ТОКОВ

Характеристики идеального и реального контуров существенно отличаются. Для контура с идеальными L и C элементами волновое сопротивление и резонансная частота определяются такими же выражениями, как и для последовательного контура:

ρ = ; ω₀ = . [6]

В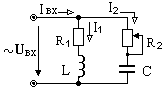 лабораторной работе сопротивления r₁ катушки и r₂ в RC-двухполюс-нике существенны, ими нельзя пренебречь. Резонансная частота такого кон-тура и его частотные характеристики определяются выражениями:

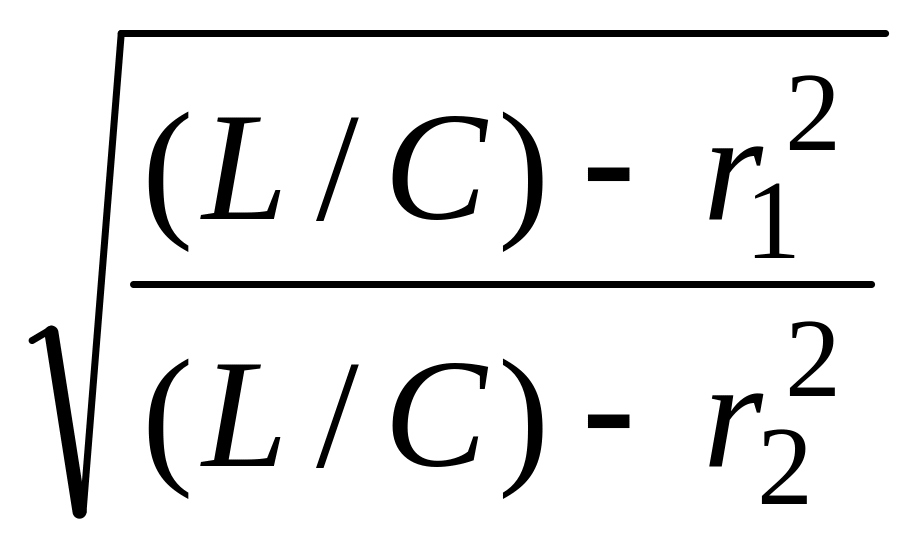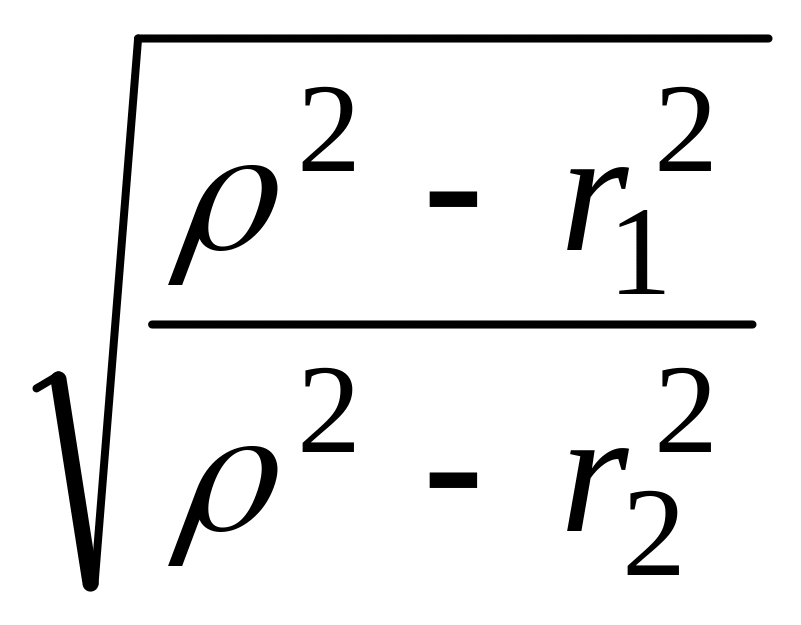ω₀′= ∙ = ω₀∙ ; [6а]

b_1L = ; b_2С = ;

Рис.4. Схема реального параллельного контура

Из выражений [1а] следует, что резонанс токов возможен лишь в случаях, когда сопротивления r₁ и r₂ оба больше или оба меньше волнового сопротив-ления ρ. На рис.5 представлен типовой вид резонансных кривых Iвх(ω), I_1L(ω), I_2C(ω) параллельного контура, приведены расчётные формулы.

Iвх(ω) = у ∙U = ∙U ; [7]

I_1L = b_2L∙U = ∙ U ; I_2C = b_2С∙U = ∙ U.

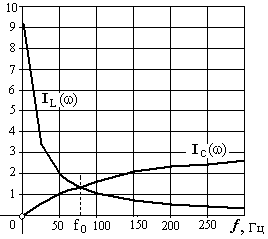Рис.5. Резонансные кривые паралл. к

В этом случае при резонансе равными по величине становятся реактивные составляющие токов I₁ и I₂. Полные токи (из-за неравенства составля-ющих I1а, I2а) могут быть и не равны между собой, но они могут значите-льно превышать общий ток цепи, который в этот момент будет наименьшим:

I вх = (g₁+g₂)∙U.

Таким образом, для параллельного контура признаками наступления резонанса токов будут наименьший общий ток цепи I и показание ваттметра Рw, которое должно быть равно произведению U вх∙I вх , поскольку в момент резонанса cos φ = 1.

* Вид кривой Iвх(ω) зависит также от добротности контура, которая у па-раллельного контура определяется как отношение проводимостей:

Q = . [8]

* Избирательность контура по кривой тока определяется как ширина полосы пропускания контура на уровне I = Iмin: Δ = f ₂ - f ₁ .

Ход работы

Исследование-расчёт режима резонанса напряжений

последовательного контура

1. Собрать схему цепи по рис.6 с последовательным соединением реостата, катушки и конденсатора, включив её на напряжение Uвх =73,32 В. Выдвигая сердечник катушки, ориентировочно найти режим резонанса, с помощью реостата установить в цепи ток Iмакс = 2.5 А, измерить напряжение на реостате U_R и определить его сопротивление R′. После этого сердечник вернуть в исходное положение.

2. Вновь выдвигая сердечник, произвести 6-7 измерений тока I, актив -ной мощности Рw, напряжений на катушке и на конденсаторе Uк и Uс.

Результаты измерений внести в табл.1.

Рис.6. Схема для исследова-

ния резонанса напряжений

3. Повторить пункты 1 и 2 работы, включив схему на напряжение Uвх = 127 В и установив в режиме резонанса ток Iмакс = 1,35-1,4 А.

Измерить напряжение на реостате U_R и определить его сопротивление R′′.

Результаты измерений также внести в таблицу 1.

Таблица 1.

Результаты измерений при исследовании резонанса напряжений

№ пп	UR = I = RR′ =					UR= I = RR′′=
	Uвх,В	I, A	Рw,Вт	Uк,В	Uс, В	Uвх, В	I, A	Рw, Вт	Uк	Uс В
1.
2.
3.
4.
5.
6.
7.
8.

4. По данным таблицы 1 построить зависимости I(L), U_L(L), U_C(L).

Расчёт индуктивности Lк, напряжения U_L по каждому эксперименту мож-но выполнить в следующем порядке:

r к = Rвх – R′ = Рw/ I² - R′;

Хк = ;

Lк = Хк /ω;

U_L = Хк ∙ I ; U_C = I ∙1/ωC.

5. Рассчитать основные характеристики последовательного колебательного контура: волновое сопротивление ρ, резонансную частоту ω ₀, частоты ω _С и ω _L, добротность Q и избирательность ∆ контура, сведя их для наглядности в итоговую таблицу 3.

Исследование-расчёт режима резонанса токов

параллельного контура

6 . Собрать схему исследуемого параллельного контура – рис.7. Вклю-чив её на напряжение Uвх = 73,32 В и, выдвигая сердечник катушки, ориентировочно найти режим резонанса, с помощью реостата в RC-ветви устано-вить в цепи ток Iмin ≈0.6 А.

После этого сердечник катушки вернуть в исход-ное положение.

Рис.7.Схема исследуемого

параллельного контура.

7. Рубильником Р₂ включить RC-ветвь. Измерить ток I_2RC, мощность Р₂, рассчитать сопротивление реостата R_2RC. Результаты внести в табл.2.

8. Включив всю цепь и выдвигая сердечник катушки, произвести 6-7 измерений тока I, активной мощности Рw и тока I₁ в ветви с катушкой.

Ток и мощность ветви с конденсатором I₂ , Р₂ при этом остаются неизменными, такими как их определили в пункте 7. Результаты измерений внести в табл.2.

Таблица 2.

Результаты измерений и расчётов при исследовании резонанса токов

№ пп	И з м е р е н о						В ы ч и с л е н о
	Uвх,В	I, A	Рw,Вт	I1RL	I2RC	Р2,Вт	R2RC	ρ, Ом	ω 0,рад/с	Q
1.	127
2.
3.
4.
5.
6.
7.

9. По данным измерений /табл.2/ рассчитать основные характеристики ρ, ω ₀, Q параллельного контура и построить резонансную кривую тока I(ω).

Необходимые для построений величины можно рассчитать по выражениям, имеющимся в пояснениях к работе.

Сопротивление R₂ имеется в таблице, а сопротивление r₁ катушки в момент резонанса можно рассчитать или принять по результатам экспериментов с последовательным контуром.

Расчёт индуктивности Lк по каждому эксперименту выполняется как обычно:

Хк = ; Lк = Хк /ω; ρ = ,

ω ₀ = ; ω₀^’= ω ₀ ∙ ; b_1L= ; b_2С = ;

Q = = ,

где I_1L, I_2C -реактивные составляющие токов ветвей в момент резонанса.

Результаты исследования характеристик последовательного и параллельного резонансных контуров для наглядности свести в итоговую табл. 3.

Таблица 3.

Основные характеристики резонансных контуров

Последовательный контур
ρ, Ом	ω 0,рад/с	ω С,рад/с	UC , В	ω L,рад/с	UL, В	Q	∆ = ω 2- ω 1

Параллельный контур

ρ = , Ом

ω 0= , рад/с

Q =

Сделать выводы по работе.

----------------------------- ♦ -------------------------------

Вопросы и задачи по расчётно-лабораторной работе № 5

1. Какие режимы в электрической цепи называют резонансными? Каким образом можно достичь резонансного режима?

2. При каких условиях в электрических цепях возникает резонанс напряжений и по каким признакам можно судить о его наступлении?

3. При каких условиях в электрических цепях возникает резонанс токов и по каким признакам можно судить о его наступлении?

4. Чем, какими величинами характеризуют колебательные контуры? Приведите их расчётные выражения.

5. Приведите и поясните вид частотных характеристик последовательного контура.

6. Приведите и поясните вид резонансных кривых последовательного контура.

7. Для схемы рис.6 по данным лабораторной работы постройте векторную диаграмму цепи в момент резонанса.

8. Для схемы рис.7 лабораторной работы постройте векторную диаграмму цепи в момент резонанса.

9. В схеме по рис.7 между средними точками ветвей включён вольтметр. Определите его показание по данным лабораторной работы в момент резонанса.

10. В схеме по рис.1: Uвх = 24В, f = 50 Гц, R =10 Ом, Х_L = 17,32 Ом. Определите необходимую ёмкость С конденсатора, чтобы в цепи наступил ре-зонанс напряжений. Рассчитайте ток, напряжения на катушке и на конденсаторе, постройте векторную диаграмму цепи.

11. В схеме по рис.4: Uвх = 24В, f = 50 Гц, R₁=10 Ом, Х₁ =17,32 Ом, сопро-тивление R₂ отсутствует. Определите необходимую ёмкость С конденсатора, чтобы в цепи наступил резонанс токов. Рассчитайте токи, постройте век-торную диаграмму цепи.

12. В схеме по рис.1: Uвх = 24В, f = var, R = 6 Ом, С=26,54мкФ, L =15,3 мГн Определите основные характеристики резонансного контура / ρ, ω₀, Q,

ω _L, ω_C / и постройте резонансную кривую тока I (ω).

----------- АВХ. 25 октября 2009г.------------

Лаборатория 311.

Лабораторная работа № 7.

ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

С ИНДУКТИВНО СВЯЗАННЫМИ ЭЛЕМЕНТАМИ

Цель работы: - экспериментально определить параметры реальных ка-тушек, имеющих индуктивную связь, найти их одноимённые зажимы и величину коэффициента связи;

- проверить расчетные соотношения, справедливые для последовательного и смешанного соединения элементов, а также для трансформаторной схемы.

Пояснения к работе

* Два элемента называют индуктивно связанными, если у них весь магнитный поток или его часть являются общими.

Кроме обычных r, x, z -параметров катушки в этом случае характеризу-ют взаимной индуктивностью М или сопротивлением Хм = wМ, или коэф-фициентом связи Ксв. Все эти величины можно рассчитать по данным первого или второго эксперимента лабораторной работы:

< 1.

* Два зажима двух индуктивно связанных катушек называются одноимён-ными (однополярными), если при одинаково направленных токах i₁, i₂ от-носительно этих зажимов магнитные потоки самоиндукции и взаимной ин-дукции в каждом элементе складываются. Это так называемые «начала» и «концы» обмоток.

Одноимённые зажимы определяются экспериментально, и для каждой пары катушек отдельно. В нашей лабораторной работе это можно сделать по результатам второго эксперимента, когда станут известны сопротивления при согласном Хсогл и при встречном Хвстр включении катушек.

* Индуктивно связанные катушки при последовательном соединении мо-гут оказывать друг на друга согласное или встречное влияние. Расчёт выполняется по закону Ома, с учётом знака сопротивления ±Хм :

;

;

* В цепях со смешанным соединением элементов, в трансформаторных схемах и в цепях с несколькими источниками энергии расчёты выполняются в комплексной форме. Расчёты ведут либо по МЗК, либо, после «развязки» связи, по закону Ома.

Правило «развязки» связи: если катушки в узел соединены разноимёнными зажимами, то для эквивалентной замены связи в ветви катушек необходимо ввести элемент +Хм, а в общую для них ветвь - элемент -Хм. И наоборот. И это не зависит от принятых направлений токов в ветвях.

Домашняя подготовка к работе

1.Изучить тему «Цепи с индуктивно связанными элементами», познако-миться с целью и пояснениями к данной лабораторной работе. Подготовить схемы и таблицы, необходимые для выполнения экспериментов.

2.В рабочей тетради выполнить расчёт цепи по Вашему варианту схемы (см. далее таблицу вариантов). Результаты расчёта занести в таблицу для сравнения с данными эксперимента в лаборатории.

Порядок выполнения работы

1. Собрать схему для определения параметров катушек – рис.1.

П одключая каждую из катушек к регулируемому источнику пос-тоянного напряжения U₀ = 1-2 B, а затем к источнику синусоидаль-ного напряжения U~10-20 B час-тотой 50 Гц, данные измерений занести в таблицу 1.

¬Рис.1.

2. По измеренным величинам рассчитать и также внести в таблицу 1 сопротивления катушек, их взаимную индуктивность и коэффициент связи, записать параметры в комплексной форме.

Таблица 1. Экспериментальное определение параметров

индуктивно связанных катушек

* * *	U0, B	I0, A	U1, В	I1, A	U2x, B	Zk, Ом	Rk, Ом	Xk, Ом	Хм, Ом	М, мГн
1катушка	0,8	0,2	15	0,272	20,5	55,1	4,0	55	75,4	240
2катушка	2,2	0,1	24	0,111	8,34	216,2	22	216	75,1	239

3. Собрать схему по рис. 2 для проверки расчётных формул, справедли-

в ых для последовательного соединения индуктивно связанных реальных ка-тушек.

На схеме разметка зажимов показана для встречного влияния катушек.

¬Рис.2

Измерения выполнить при напряжении U~ = 20-24 B, 50 Гц

как для согласного, так и для встречного включения катушек.

Принимая rсогл = rвстр = r₁+ r₂ из первого эксперимента, по данным из-мерений вычислить индуктивные сопротивления цепи при согласном и при встречном влиянии элементов и значение взаимной индуктивности М .

; ; ;

Результаты измерений и расчётов внести в таблицу 2.

Таблица 2.

Результаты исследования цепи при согласном и встречном

последовательном соединении катушек

Последовательное соединение		Uвх В	I, мA	U1, B	U2, B	Х, Ом
Согласное	Расчёт	24	56,9	7,42	16,61	421,8
	Эксперимент	24
Встречное	Расчёт	24	195	4,05	27,75	120,2
	Эксперимент	24

Сопоставить значения токов Iсогл и Iвстр в таблице 2 и сформулировать порядок определения одноимённых зажимов различных обмоток.

4. Далее исследование выполняется в двух вариантах: чётные номера зве-ньев работают со схемой, представляющей смешанное соединение элементов (рис. 3); нечётные варианты исследуют трансформаторную схему в режиме короткого замыкания (рис.4).

Таблица вариантов схем со смешанным соединением

индуктивно связанных элементов

4а. Собрать схему цепи со смешанным соединением индуктивно связан-ных элементов, рассчитанную в домашней подготовке к работе. Резисторы R₁= 100 Ом или R₂= 200 Ом, конденсаторы С₂= 10 мкФ или С₃ = 20 мкФ, указанные в схеме, взять из блока пассивных элементов стенда. При напряжении Uвх= 30 В измерить токи в ветвях схемы. Результаты измерений вне-сти в табл.3 для сравнения с их значениями, рассчитанными ранее.

Таблица 3.

Расчётные и измеренные значения токов в схеме со смешанным

соединением индуктивно связанных элементов

Вариант 09	Uвх, B	I1, A	I2, A	I3, A	P2-1, Вт
Эксперимент	24				--
Расчёт	24	0,41	0,207	0,235	2,554

Для схемы рис.3 построить полную векторную диаграмму цепи.

4б. Трансформаторную схему включения индуктивно связанных катушек (рис.4) будем исследовать в следующем порядке: сначала в лаборатории проводим измерения, а затем, по параметрам катушек, полученным в первом эксперименте, выполняем домашний проверочный расчёт.

В качестве примера, пусть: Uвх = 24B, 50 Гц, r₁ = 4 Ом , Х₁ = 55 Ом,

r₂ = 22 Ом, Х₂ = 216 Ом, Хм = 75.4 Ом.

.

*Трансформатор описывается дву-мя уравнениями по II закону Кирх-гофа:

Отсюда выражения токов:

А

* Активная мощность, потребляемая трансформатором из сети:

Р₁ = Re Вт

Активная мощность, передаваемая через узел связи во вторичную обмотку

= - Хм^. I₁∙ I2 ∙ sin (y₁ - y₂) =

= - 75,4^. 0.808^. 0,28 sin (-77,06 – [-71,244] ) = 1,732 Вт.

Все расчётные и измеренные величины для сравнения заносим в табл.4.

Результаты расчёта и измерений Таблица 4.

при трансформаторной схеме включения катушек

Трансформатор	U1, B	I1, A	P1, Вт	I2, A	Р1-2,Вт
Эксперимент	24	0,8	---	0,28	---
Расчёт	24	0,808	4,342	0,28	1.73

Как видно из таблицы, расчётные величины практически совпадают с из-меренными в эксперименте.

Заключение по работе.

В первом эксперименте лабораторной работы определены параметры ка-тушек, имеющих индуктивную связь: Zкат, Rкат, Xкат, Xм.

Во втором эксперименте проверены формулы расчёта Zсогл, Zвстр и определены одноимённые зажимы катушек.

В третьем эксперименте подтверждена пригодность развязки связи для расчёта цепей со смешанным соединением индуктивно связанных элементов. Проверен также расчёт трансформаторной схемы по законам Кирхгофа. Результаты отражены в таблицах 3 и 4.

Вопросы и задачи по лабораторной работе

1. В чём сущность явлений самоиндукции и взаимной индукции?

2. Поясните сущность «ёмкостного эффекта» в цепях с индуктивно связанными элементами. Возможен ли ёмкостный эффект в условиях третьего экспериментов лабораторной работы?

3. Каким образом определяются одно-имённые зажимы катушек?

4. На примере приведенной слева схе-мы поясните, как определить одноимён-ные зажимы и взаимную индуктивность

М обмоток трансформатора.

5 . Поставлены три эксперимента, результаты которых указаны на схемах. Определите Хм, укажите, согласно или встречно включены катушки в третьем эксперименте, разметьте зажимы катушек.

6. Каково условие передачи активной мощности через узел связи и чему равно Рм_1-2 во втором эксперименте при встречном включении катушек?

7. Как можно проверить передаваемую мощность Рм_1-2 в условиях третье-го эксперимента?

8. Как определяется знак напряжения взаимной индукции в уравнениях, со-ставляемых по II закону Кирхгофа? /правило знака слагаемого ±Zм Iq /.

9. Сформулируйте правила развязки связи и укажите, зачем она нужна и когда она целесообразна.

10. Определите входное сопротивление исследуемой трансформаторной схемы.

-------------- Скорректировано. АВХ, 9 мая 2012г.

Лаборатория 311.

ЛАБОРАТОРНАЯ РАБОТА № 11.

ИССЛЕДОВАНИЕ ЦЕПИ

ПРИ НЕСИНУСОИДАЛЬНОМ ВХОДНОМ НАПРЯЖЕНИИ

Цель работы: - проверка методики разложения в ряд Фурье пери-одических несинусоидальных функций и исследование влияния индуктивности и ёмкости на форму кривой тока в цепи.

Пояснения к работе

Методика расчёта линейных электрических цепей при несинусоидальных напряжениях или токах состоит в том, что заданное несинусоидальное воздействие представляют в виде гармонического ряда Фурье, расчёт цепи выполняют по каждой гармонике в отдельности, пос-ле чего записывают результирующие выражения мгновенных значе-ний iнеsin, uнеsin, и находят действующие значения величин Iнеsin Uнеsin.

[1]

Здесь А_1т sin(ωt+ψ₁) - первая гармоника, которую называют основной, так как она имеет период, равный периоду исследуемого сигнала. Ряд называется дискретным, так как все последующие гармоники ряда в целое число раз по частоте отличаются от основной. Раскрывая синусы суммы углов по каждой гармонике, получим запись ряда в более удобном виде, через синусные и косинусные составляющие с нулевыми начальными фазами:

[1а]

Если несинусоидальное напряжение или ток имеют типовую форму, то их представление рядом Фурье можно найти в учебнике или справочнике.

Если же несинусоидальная функция получена экспериментально, в виде осциллограммы, то её разложение в ряд Фурье выполняется графоаналитическим способом, по приближённым формулам, где интегралы заменяются конечными суммами слагаемых. А₀ - постоянная составляющая ряда;

Коэффициенты ряда: А₀ - постоянная составляющая ряда,

- косинусная составляющая,

- синусная составляющая ряда

определяются интегральными выражениями, или, приближённо, как конечные суммы fq (ωt).

≈ = ;

Вк_т = ≈ ; [2]

Ск_т = ≈ ;

Через синусные и косинусные составляющие далее рассчитываются амплитуда и начальная фаза по каждой гармонике ряда:

[3]

В зависимости от требуемой точности разложения, период функции разбивают на n = 12- 24 -36 интервалов. Если функция обладает каким-либо ви-дом симметрии: относительно оси абсцисс, оси ординат или относительно начала координат, то её разложение в ряд упрощается. Во-первых, можно исследовать лишь полупериод или даже четверть периода функции, причём, по тем же формулам [2-3], а во-вторых, не надо будет рассчитывать не-которые слагаемые ряда.

* При расчёте цепи несинусоидального тока следует помнить о том, что индуктивное и ёмкостное сопротивления зависят от частоты:

Х_L⁽⁰⁾ = 0, Х_L^(к) = К ∙Х_L⁽¹⁾ , Х_С⁽⁰⁾ = ∞, Х_L^(к) = Х_С⁽¹⁾/ к.

Из этого следует, что индуктивность подавляет высшие гармоники в кри-вой тока, делая её по форме близкой к виду первой гармоники подаваемого напряжения. Ёмкость, наоборот, способствует увеличению доли высших гармоник в кривой тока, чем делает её более искажённой в сравнении с кри-вой питающего напряжения.

Действующие значения несинусоидального тока и напряжения рассчитываются через действующие значения всех входящих гармоник, и не зави-сят от их начальных фаз:

; ; [4]

В лабораторной работе несинусоидальное входное напряжение получа-ют с помощью дросселя (катушка с ферросердечником). При подаче на дрос-сель синусоидального напряжения, ток (при насыщении сердечника) стано-вится несинусоидальным, и имеет сильно выраженную пикообразную фор-му. Напряжение, снимаемое с резистора R, повторяет эту форму кривой.

Пример графоаналитического разложения несинусоидальной кривой напряжения сложной формы в ряд Фурье.

С хема цепи для получения

несинусоидального

напряжения

Как видим, полученная осциллограмма напряжения u(t) - это периодиче-ская несинусоидальная функция, симметричная относительно оси абсцисс и начала координат. Следовательно, при разложении в ряд кривая не будет содержать постоянной составляющей и чётных функций, и при этом достаточно будет исследовать лишь полупериод функции. Разбиваем его, напри-мер, на n = 6 равных интервалов с ∆ωt =30 ⁰, мгновенные значения напряжений uq(ωt) снимаем в конце каждого интервала. По формулам 2 рассчитываем коэффициенты ряда В_1т , С_1т для первой гармоники, В_3т , С_3т для третьей гармоники и т.д. Расчёты по каждой гармонике сводим в таблицы.

Таблица 1. Расчёт первой гармоники.

**	ωt, град	uq(ωt), B	uq·sinq(ωt)	uq·cosq(ωt)
1.	30	7,5	3,75	6,5
2.	60	25,5	22,08	12,75
3.	90	63,0	63,0	0
4.	120	32,1	27,8	-16,05
5.	150	8,0	4,0	-6,93
6.	180	0	0	0
= 40,21 B = - 1,243 B

По формулам [3] считаем амплитуду и начальную фазу первой гармони-ки. Величину угла ψк считаем с учётом знаков sin и cos - составляющих:

= 40,23 В = -1,77 ⁰.

Таблица 2. Расчёт третьей гармоники.

**	ωt, град	uq(ωt), B	uq·sinq(3ωt)	uq·cosq(3ωt)
1.	90	7,5	7,5	0
2.	180	25,5	0	-25,5
3.	270	63,0	-63	0
4.	360	32,1	0	32,1
5.	450	8,0	8,0	0
6.	540	0	0	0
= -15,83 B = + 2,2 B

= 15,982 В = +172,1 ⁰.

Итак, выражение несинусоидального напряжения, рассчитанного с точностью до 3-ей гармоники, будет:

Чтобы убедиться в правильности выполненного разложения, рассчитаем действующее значение напряжения и построим расчётную кривую напряжения, сравнив их с полученными экспериментально.

.

Расчётный график входного напряжения u(t) .

Обратим внимание на следующее: первая и третья гармоники сдвинуты почти на 180⁰, т.е. находятся почти в противофазе. Именно в таком случае несинусоидальная функция получается пикообразной. В противном случае несинусоидальная кривая получается уплощённой.

Подготовка к работе и порядок выполнения

1. В домашней подготовке к работе необходимо изучить тему «Электри-ческие цепи при несинусоидальных ЭДС и токах». Вычертить схему источ-ника несинусоидального напряжения и подготовить таблицы для расчёта 1,3 и 5-ой гармоник и формулы для их расчёта.

2. В лаборатории собрать схему с источником несинусоидального напря-жения. На вход источника подать синусоидальное напряжение частотой 50 Гц от одной из фаз 3х-фазного источника, имеющегося на стенде. В качестве ре-зистора R, с которого снимается несинусоидальное напряжение, сформиро-вать (параллельным соединением) сопротивление 20-25 Ом.

3. Из съёмных элементов стенда, в соответствии с вариантом, сформировать исследуемую RL или RС-нагрузку.

Таблица 1. Варианты нагрузки

Параметры	1вариант	2вариант	3вариант	4вариант
R1, Ом	51	51	51	51
rк, Ом	4	52	4.5	22
L, мГн	175	100	120	0.69
rС, Ом	200	100	150	75
С, мкФ	2	4.5	2.5	5

4. Регулируя подаваемое напряжение, добиться на осциллографе кривой входного несинусоидального напряжения uнеsin c параметрами, близкими к изображённым на рисунке. Записать масштабы по напряжению m_u и по вре-мени m_t, определяемые положением переключателей осциллографа, и снять кривую с экрана осциллографа для домашней обработки. Измерить и внес-ти в таблицу 2 действующее значение напряжения (Uнеsin ≈ 5-10В).

Таблица 2. Амплитуды гармоник входного неsin-напряжения.

Действующие значения напряжения и токов нагрузки

Исследуемые величины	Um(1), B	Um(3), B	Uнеsin, B	IRL, мА	IRС, мА
Эксперимент	---	---
Расчёт

5. Подключая RL, а затем RС-нагрузку, с резистора R₁ снять кривые токов и измерить их действующие значения I_RL и I_RС. Измеренные величины для сравнения и анализа внести в таблицу 2.

6. Сравнивая величины и графики токов в RL- и RС- нагрузках, сделать вывод о влиянии индуктивности и ёмкости на форму кривой тока.

7. При оформлении отчёта по работе, полагая кривую напряжения uнеsin заданной, выполнить расчёты, необходимые для заполнения таблицы 2.

Вопросы по лабораторной работе для самопроверки

1. Почему в лабораторной работе при разложении осциллограммы в ряд Фурье не рассчитывали нулевую и вторую гармоники?

2. Какое значение несинусоидального тока измеряет амперметр магнито-электрической системы? Рассчитайте это значение, если i = 4sin(ωt) -2 sin(3ωt).

3. Какие значения несинусоидального напряжения измеряют вольтметры электромагнитной и электродинамической систем? Рассчитайте показание электромагнитного амперметра, если i = 4sin(ωt) - 2 sin(3ωt).

4. Как изменяется индуктивное и ёмкостное сопротивление току разных гармоник?

5. Сопротивление цепи для токов 5^й гармоники: Z⁽⁵⁾ = 10 - j10 Ом. Определите сопротивление цепи для токов 2^й гармоники.

6. Как влияют индуктивность и ёмкость на форму кривой несинусоидального тока в сравнении с кривой напряжения?

7. Определите действующее значение несинусоидального напряжения u(t) = 100 +200 sin(ωt - 30⁰) - 100 sin(3ωt + 45⁰) В.

--------------------- АВХ, 26 мая 2012г. ---------------------

Ремарка. Цель работы и таблицу вариантов надо доработать.

Лаборатория 311.

Расчётно-Лабораторная Работа № 17

ИССЛЕДОВАНИЕ пассивного ЧЕТЫРЕХПОЛЮСНИКА

Цель работы: определить характеризующие 4-полюсник коэффи-циенты и передаточные W(jω) функции. Составить схему замещения четырехполюс­ника.

Пояснения к работе

Четырехполюсником называют электрическую цепь или её часть любой конфигурации, у которой выделены два входных и два выходных зажима.

Четырехполюсник можно характеризовать А,В,С,D - коэффициентами (первичные параметры), характеристическими (волновыми) параметрами Zc, g = а + jb и передаточными функциями W (jω) по напряжению и по току.

Уравнения, связывающие напряжения и токи на входе и выходе 4-полюсника (как симметричного, так и несимметричного), при любой нагрузке, записанные в А-форме, имеют вид:

│ ;

│ ; (17.1)

А, В, С, D - комплексные коэффициенты, характеризующие 4-по-люсник на данной частоте. У линейных пассивных четырёхполюсни-ков они подчиняются соотношению:

(17.2)

Коэффициенты четырехполюсника могут быть определены чисто аналитически по его схеме и заданным параметрам элементов:

А = ; В = А∙Z_2к; . (17.3)

Здесь Z_1Х, Z_2Х - комплексы входного сопротивления четырехполюсника в режиме холостого хода относительно входных и выходных зажимов; Z_2К - комплекс входного сопротивления четырехполюсника относительно выходных зажимов, когда входные зажимы замкнуты накоротко.

У симметричного четырёхполюсника равны его сопротивления

Z_1Х = Z_2Х = Z_ХХ, Z_1К = Z_2К = Z_КЗ и коэффициенты А = D.

Если схема четырёхполюсника неизвестна, его А,В,С,D- коэффициенты могут быть рассчитаны по данным соответствующих опытов ХХ и КЗ.

Для исследования различных режимов работы 4-полюсника обыч-но пользуются трёхэлементными Т- и П- схемами замещения, параметры которых находят по следующим выражениям:

Т- схема: ; (17.4)

П- схема: (17.5)

Естественно, что если 4-полюсник представляет собой стандарт-ную Т- или П- схему, то его А,В,С,D- коэффициенты проще найти из соотношений (17.4 или 17.5).

* Если устройства, представляемые четырёхполюсниками, работа-ют в широком диапазоне частот (усилители, электрические фильтры, длинные линии), удобнее пользоваться характеристическими (волно-выми) параметрами 4-полюсника:

Z_С1, Z_С2 - характеристические сопротивления несимметричного 4-полюсника со стороны входных и со стороны выходных зажимов;

g = а + jb - постоянная передачи 4-полюсника, безразмерная величина, характеризующая передачу сигнала по мощности:

По определению постоянная передачи

g = а+jb = ½ ℓп = ½ ℓп , (17.6)

причём, по модулю: а =½ ℓп = ½ ℓп , Нп.

а - коэффициент затухания (ослабления) сигнала по мощности в неперах [Нп], белах [Б ] или децибелах [дБ ].

1 Нп = 8.686 дБ, 1 дБ = 0.115 Нп.

b - коэффициент изменения фазы “мощностного” сигнала при прохождении через четырёхполюсник:

b = ½ [(ψu1 - ψu2) + (ψ_i1 - ψ_i2)], рад.

Уравнения симметричного 4-полюсника в А-форме, записанные через его волновые параметры, имеют вид:

│U₁ = U₂ ch g + Zc∙I₂ sh g;

│I ₁ = U₂ (sh g /Zc) + I₂ ch g; (17.1a)

Характеристические параметры 4-полюсника могут быть рассчитаны через А,В,С,D- коэффициенты или непосредственно по дан-ным опытов ХХ и КЗ.

(17.7)

g = а + jb .

По данным опытов холостого хода и короткого замыкания мож-но находить как характеристические параметры Z_C и g = а + jb , так и первичные А,В,С,D- коэффициенты четырёхполюсника:

(17.8)

.

или

А = ; В = А∙Z_2к; . (17.3)

* Рассмотренные А,В,С,D- коэффициенты и волновые параметры Z_C и g = а + jb характеризуют непосредственно сам 4-полюсник. Но он может быть включён и на произвольную несогласованную нагруз-ку, от чего затухание сигнала изменится. Чтобы охарактеризовать передачу сигнала при произвольной нагрузке, пользуются понятием коэффициентов передачи по напряжению Кu и по току Кi, или в об-щем случае – передаточными функциями W(jω).

К_u = = ; К_i = = ; (17.9)

В лабораторной работе в качестве нагрузки используется резис-тор R_нг = 100 Ом.

Задания по лабораторной работе № 17 «Исследование 4-полюсников»

Нечётные 1, 3, 5, 7 варианты

Схема, параметры
r1, Ом	100 Ом [ 03 ]	20 Ом [ R4 ]	300 Ом [ 03 ]	510 Ом [ 07 ]
r2, Ом	100 Ом [ R4 ]	--	300 Ом [ R4 ]	--
L, мГн	--	690 мГн [ L2 ]	--	--
С1, мкФ	20 мкФ	10 мкФ [ С4 ]	20 мкФ [ С3 ]	20 мкФ [ С3 ]
С2, мкФ	--	10 мкФ [ С2 ]	10 мкФ [ С2 ]	10 мкФ [ С2 ]
Uвх, В	36 В f =50Гц	24 В f =50Гц	24 В f =50Гц	36 В f =50Гц

Чётные 2, 4, 6, 8 варианты задания

Схема, параметры	Т- схема, симметричный	П- схема, симметричный	П- схема, симметричный	Т- схема, симметричный
Zxх, Ом	187.832 φ = -57.8330	78.616 φ = -81.620	156.7 φ = -9.440	601.0 φ = -31.940
Zкз, Ом	177.473 φ = -14.710	667.473 φ = +76.630	99.95 φ = -70.540	565.31 φ = -75.370
Uвх, В	36 В f =50Гц	24 В f =50Гц	24 В f =50Гц	36 В f =50Гц

Домашняя подготовка к работе

При подготовке к работе необходимо внимательно изучить изло-женные выше пояснения к работе, чтобы правильно использовать приведенные расчётные формулы.

Расчёты величин, характеризующих 4-полюсник, рекомендуется выполнять в следующем порядке:

- рассчитать АВСD-коэффициенты (17.3), проверив их по соотно-шению 17.2. По выражениям (17.7 или 17.8) найти характеристические параметры Z_C1, Z_C2 и g = а + jb четырёхполюсника;

- рассчитать элементы и составить Т- или П-схему замещения 4-полюсника, указав, реализуема ли она в лабораторных условиях;

- рассчитать коэффициенты передачи Кu и Кi четырёхполюсника при Rнг = 100 Ом;

- при напряжении Uвх, указанном в варианте задания, по уравне-ниям 17.1 или с помощью коэффициентов передачи Кu и Кi рассчи-тать токи и напряжения в трёх режимах:

- при холостом ходе I_1X, U_2X; - при коротком замыкании I_1К, I_2К;

- при Rнг = 100 Ом -- I₁, U₂, I₂.

Результаты расчётов внести в таблицы 1 и 2.

Таблица 1

Основные параметры 4-полюсника

Характеристики 4-полюсника	А , б/р	В , Ом	С , См	D , б/р	ZC1 Ом	ZC2 Ом	g=а+jb
Расчёт

Таблица 2

Исследование режимов работы 4-полюсника

Режимы 4-полюсника		Uвх, В	I1, мА	Zвх, Ом	U2 , В	I2 , мА
Холостой ход	расчёт	36	191.7	187.83	30.48	0
	экспер.
Короткое замыкание	расчёт	36	202.8	177.47	0	172
	экспер.
Rнг =100 Ом	расчёт	36	187.8	191.48	11.7	117
	экспер.

В нечётных вариантах задания исходными данными являются заданная схема 4-полюсника и параметры её элементов.

В чётных вариантах расчёты выполняются по заданным сопротивлениям холостого хода Z_ХХ и короткого замыкания Z_КЗ.

Ход выполнения работы

1. Подобрать необходимые элементы из имеющихся на стенде, и собрать схему замещения 4-полюсника, рассчитанную в домашней подготовке.

2. С помощью блока трёхфазных напряжений установить напря-жение U_вх = 24 ÷ 36В, f = 50 Гц и произвести измерения входного тока I₁, а также напряжения U₂ и тока I₂ на выходе 4-полюсника в трёх режимах: холостой ход, короткое замыкание, работа при сопротивлении Rнг = 100 Ом.

3. Заполнить таблицу 2 и сравнить расчётные и измеренные величины. Сформулировать выводы по работе.

Вопросы для самоконтроля

1. Что называют четырехполюсником, какими величинами его характери-зуют?

2. Напишите основные уравнения 4-полюсника в А-форме как при питании со стороны первичных зажимов, так и при питании со стороны вторичных зажимов.

3. В чём смысл гибридных h-параметров 4-полюсника? Как перейти к уравнениям в Н-форме, если известны АВСD - коэффициенты 4-полюсника /Атабеков Г.И., ТОЭ, 1979г., с.575/.

4. Как определяются АВСD - коэффициенты четырехполюсника экспери-ментально?

5. Как связаны между собой коэффициенты четырехполюсника?

6. Почему схемы замещения 4-полюсника можно сформировать из трёх элементов? Как рассчитывают параметры Т- и П-схем замещения.

7. Какие величины называют волновыми параметрами 4-полюсника, как они рассчитываются и когда их применение необходимо?

8. Что понимают под передаточными функциями 4-полюсника, что они характеризуют, как рассчитываются и когда их применение необходимо?

--------------------------------- ♦ ---------------------------------

Лаб.работа №17 - 6стр. Σ23часа. 8 - 12 февраля 2011 года.

------- Лаборатория 311.

РАСЧЁТНО-Лабораторная работа № 20

«ИССЛЕДОВАНИЕ ЭЛЕКТРИЧЕСКИХ ЧАСТОТНЫХ ФИЛЬТРОВ»

Цель работы - расчёт рабочих характеристик а(ξ), b(ξ), Zс(ξ), Кu(ξ) филь-тра типа “К” и экспериментальная проверка его фильтрующие свойства.

Пояснения к работе

Частотные электрические фильтры - это четырёхполюсники, чаще всего построенные из LС-элементов, и пропускающие к приёмнику сигналы не всех частот, а лишь определённого диапазона. Основные свойства фильтра определяются произведением продольного сопротивления на поперечное: Z₁Z₂ = K = const или Z₁Z₂ = φ(ω). По основным свойствам различают фильтры типа k и фильтры типа m, по пропускаемым частотам - фильтры нижних частот (НЧФ), фильтры высоких частот (ВЧФ), а также полосовые и заграждающие филь-тры.

Фильтры характеризуют номинальным характеристическим сопротивлением ρ и частотой среза ωср, fср, которая является граничной между зо-ной прозрачности и зоной затухания фильтра. Рабочими характеристиками фильтра называют зависимости коэффициента затухания a(ω), коэффициента фазы b (ω) и характеристического сопротивления Zс(ω).

О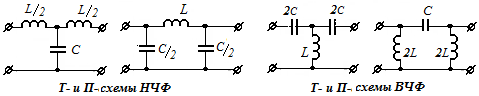 братим также внимание на то, что у фильтров различают расчётные Lрасч, Срасч и конструктивные параметры. На приведенных типовых Т и П-схемах LС-фильтров типа k указаны конструктивные параметры.

Номинальные характеристические сопротивления и частоты среза фильтров рассчитываются через расчётные величины Lрасч, Срасч:

ρ_НЧФ = Zс(ω = 0) = ; ρ_ВЧФ = Zс(ω = ∞) = ;

ω_{ср НЧФ} = ω ₀ = ; ω_{ср ВЧФ} = ω ₀ = ;

На рисунках ниже приведен типовой вид рабочих характеристик фильтров, а также формулы, по которым выполняется их расчёт.

Выражения и графики рабочих характеристик низкочастотных фильтров

В ыражения и графики рабочих характеристик высокочастотных фильтров

В качестве примера приведём расчётную таблицу для построения

характеристик НЧ- фильтра с параметрами ρ = 158 Ом, fср = 100.7 Гц.

№ пп	Низкочастотный фильтр Т- и П- схемы	Зона прозрачности фильтра		Гранична частота	Зона затухания фильтра
1.	Частота: f, Гц	0	50	100.7 Гц	150	250
2.	ω, рад/с	0	314	632.4	942.5	1570.8
3.	ξ = f / f ср	0	0.5	1.0	1.49	2.48
4.	К.затух. ch а(ξ) = 2 ξ 2 - 1, Нп	0	0	0	1.907	3.12
5.	К. фазы cos b = 1 - 2 ξ 2, рад	0	60 0	+ π	+ π	+ π
6а.	ZсП (ξ) = ρ / , Ом	158	182.4	∞	-j141	-j68.9
6б.	ZсТ (ξ) = ρ ∙ , Ом	158	137.2	0	+j447	+j774
7а	Снг, мкФ	--	--	--	7.51	9.232
7б	Lнг, Гн	--	--	--	0.474	0.493
	Zнг = Zсп (ξ)	Согласованная нагрузка
8.	Кu (ξ) = е – а (ξ)	1	1	1	0.1485		0.0441
9.	Напряжение на выходе U2m(ξ)	---	20 В	---	0.99		0.088

Рабочие характеристики а (ω), b (ω), Zс (ω) конкретного фильтра - это известные типовые кривые, только с конкретными значениями величин.

Обычно фильтр рассчитан на работу при согласованной нагрузке: Zнг = = Zс. Но волновые сопротивления Zc_п (ξ) и Zc_т (ξ) в зоне пропускаемых частот, как видим, у обоих типов фильтра значительно изменяются с частотой, и согласовать фильтр с его нагрузкой по всему диапазону пропускаемых частот практически невозможно.

Для оценки фильтра в условиях несогласованной нагрузки используются его амплитудно-фазовые частотные характеристики - АФЧХ:

К u = = А(ω)∙е ^jφ(ω) ; К i = = В(ω)∙е ^jφ(ω) ;

---------------------- ♦ ----------------------

В лабораторной работе будем полагать, что в зоне прозрачности фильтры работают на «почти согласованную» нагрузку.

Для выработки сигнала, содержащего 1-ю, 3-ю и 5-ю гармоники, в лаборатории используется катушка L₄ с насыщенным сердечником (дроссель), питаемая от регулируемого источника напряжения u(t) частотой 50 Гц.

Согласованное сопротивление нагрузки Rнг.согл устанавливается с помощью переменного резистора R₄ на стенде.

Исследование фильтрующих свойств схем предполагается выполнить качественно, наблюдая и сравнивая осциллограммы напряжений на входе и на выходе фильтра.

Таблица вариантов (параметры конструктивные)

1вариант	2вариант	3вариант	4вариант
НЧФ, Т-схема	ВЧФ, Т-схема	ВЧФ, П-схема	НЧФ, П-схема
0.175 Гн	0.175 Гн	50 мГн	0.69 Гн
30 мкФ	4.5 мкФ	10 мкФ	10 мкФ

Подготовка к работе и порядок выполнения

1. В домашней подготовке к работе необходимо изучить тему «Электри-ческие частотные фильтры». Пользуясь конструктивными параметрами своего варианта фильтра рассчитать величины ρ, fср, ωср, а также построить гра-фики рабочих характеристик а(ω), b(ω), Zс (ω) фильтра (см. пример выше).

2. Пользуясь конструктивными параметрами фильтра, указанными в варианте, собрать исследуемую схему фильтра. Сопротивление согласованной нагрузки Rнг.согл принять равным волновому сопротивлению на основной пропускаемой фильтром частоте. Для НЧФ это будет Zc (50Гц), для ВЧФ - Zc (150Гц). Установить Rнг.согл с помощью переменного резистора R₄.

3. Собрать схему с источником несинусоидального напряжения. Регули-

руя подаваемое напряжение, добиться на осциллографе кривой входного не-синусоидального напряжения uнеsin c параметрами, близкими к изображённым на рисунке. Измерить действующее значение напряжения: Uнеsin ≈ 5.7В.

Разложение такого напряжения в ряд Фурье даёт следующее выражение:

uнеsin = 7.6 sin(314t + 10⁰) + 2.54 sin(3ωt - 150⁰) + 0.75 sin(5ωt + 42⁰) В.

Это напряжение следует принять в качестве базового для всех вариантов.

4. Подать на вход фильтра исследуемое напряжение. С помощью вольтметра измерить действующие значения напряжений Uвх и Uвых. С экрана осциллографа снять и проанализировать кривые напряжений uвх и uвых(t).

Указание: на каждой из осциллограмм должны быть приведены масштабы по напряжению m_u и по времени m_t, определяемые положением переключателей ос-циллографа.

4а. Заменить низкочастотный фильтр высокочастотным П-образным фильтром и по его параметрам (4вариант) определить f₀ и ZсП на частоте f = 150 Гц.

f₀ = , ρ = ; Z_CП = .

С экрана осциллографа снять и объяснить форму напряжения uвых(t) ВЧ-фильтра.

5. В отчёте следует привести:

- цель работы;

- схему фильтра, таблицу расчёта и построенные графики рабочих характеристик;

- схему источника несинусоидального напряжения;

- графики напряжений uвх(t) и uвых(t), расположив их один под другим для удобства сравнения;

- выводы о фильтрующих свойствах исследованных фильтров.

--------------------------- ♦ -------------------------

Вопросы по лабораторной работе для самопроверки

1. Дайте определение частотного электрического фильтра. Какими параметрами характеризуется четырехполюсник именно как фильтр?

2. Каким образом по схеме LС-фильтра определить, является ли фильтр низкочас-тотным или высокочастотным?

3. Какой интервал частот называется полосой пропускания фильтра?

4. Почему на практике нельзя осуществить согласование фильтра с нагрузкой по всей полосе пропускания фильтра?

5. По определению коэффициент затухания а = ½ ℓn S₁/S₂, т.е. характеризует затухание сигнала по мощности. Полагая напряжение U₁ = 10В, а = 10 дБ, определите напряжение на выходе фильтра при согласованной нагрузке.

6. В лаборатории для экспериментов выданы две индуктивнос­ти по 20 мГн и два конденсатора по 2 мкФ. Сколько П и Т-схем фильтров можно составить из этих эле-мен­тов? Нарисуйте эти схемы. Ответ № 4.1.

7. Для НЧ- фильтра по Т-схеме, имеющего две индуктивности по 20 мГн и два конденсатора по 2мкФ, определите параметры f₀, ω₀, ρ, Zнг.согл. и приведите ти-повой вид его рабочих характеристик. Ответ № 4.9 в конспекте лекций.

8. Для НЧ-фильтра по Т-схеме известно: f₀ =1125.4 Гц, на частоте f₁ = 2 f₀ сопро-тивление Zнг.согл = +j245 Ом. Определить конструктивные параметры L и С филь-тра, найти коэффициент затухания а(f₁) и коэффициент фазы b(f₁). Ответ № 4.7.

9. Составьте П-схему ВЧФ с частотой среза f₀ = 397.9 Гц, если имеются две индуктивности по 20 мГн и два конденсатора по 2 мкФ. Определите Zс_П(ω) сопротив-ление фильтра на частотах 0 и ∞ . Ответ № 4.6.

10. Сигнал uвх=10sin(314t)+3.6sin (942t - 60⁰) В подаётся на вход НЧ - фильтра, с частотой среза f₀ = 100 Гц. К согласованной нагрузке на выходе фильтра подключён вольтметр электромагнитной системы. Запишите выражение выходного напря-жения uвых(t) и найдите показание вольтметра Uv.

11. Сигнал uвх=10sin(314t)+3.6sin (942t - 60⁰) В подаётся на вход ВЧ - фильтра, с частотой среза f₀ = 100 Гц. К согласованной нагрузке на выходе фильтра подключён электромагнитный вольтметр. Запишите выражение uвых(t) и найдите Uv. .

12. На вход НЧ -фильтра, собранного по П-схеме и имеющего два конденсатора по 10мкФ, подан сигнал с напряжением: uвх=10sin (314 t) + 5sin (942t - 60⁰) В. Известно, что на частоте 150Гц сопротивление Zнг.согл = -j142,34 Ом, а выходное на-пряжение третьей гармоники uвых⁽³⁾ = 0,73 sin (942t - 240⁰) В. Определить L и С, найти волновое сопротивление ρ и частоту среза ω₀ фильтра. Ответ № 3.1.

--------------------------- ♦ АВХ, 13 мая 2012 года ♦-----------------------------

ЛІТЕРАТУРА

1. Атабеков Г.И. ТОЭ. Линейные электрические цепи. -М. Энергия, 1979.

2. Бессонов Л.А. ТОЭ. Теоретические основы электротехники. Электрические цепи. - М.: Высшая школа, 1984. – 525с.

3. В.Х. Антамонов. Конспект лекций и примеры расчёта по теории электрических цепей и сигналов - 2012г. Электронный вариант.

4. Методические указания по выполнению расчётно-лабораторных работ по теоретической электротехнике. ч.1. - Дон НТУ, 2002. – 72с. (МУ-648).

5. Методические указания по выполнению расчётно-лабораторных работ по теоретической электротехнике. ч.2. - Дон НТУ, 1988. – 63с. (МУ-142а).

6. Методические указания и домашние задания для выполнения домашних заданий по теоретической электротехнике. - Донецк: Дон НТУ, 2010. – 96с. (МУ-126).

------------------------- ♦ --------------------------

СОДЕРЖАНИЕ

Общие сведения о стенде УИЛС-2 …………………………… 3

Образец титульного листа отчёта о лабораторной работе ….. 6