Элементы теории экстремальных задач
1. Основные определения
Множество, между элементами которого установлены определенные соотношения, называют пространством.
Множество, элементами
которого являются всевозможные наборы
из
действительных чисел
(1)
причем каждой паре
элементов
,
этого множества поставлено в соответствие
действительное число
:
,
(2)
называется n-мерным
вещественным пространством
.
Число
называется расстоянием между элементами
множества и удовлетворяет следующим
аксиомам:
1)
,
тогда и только тогда, когда
;
2)
;
3)
.
Число
называют размерностью
пространства
.
Элемент
называют точкой
пространства. Элемент
называют нулевым элементом пространства
.
Множество, в котором введено расстояние,
называют метрическим
пространством.
Пространство
в котором
– числовая
прямая,
пространство
в котором
–
плоскость,
пространство
для которого
–
обычное трехмерное
пространство.
Пусть дана точка
и число
.
Множество всех точек
,
таких, что
,
называется
-окрестностью
точки
в пространстве
и обозначают
.
Для элементов пространства можно ввести понятия суммы элементов
,
(3)
и произведения на действительное число:
,
и
.
(4)
Множество элементов , в котором сумма и произведение на число определены формулами (3), (4) называется линейным векторным пространством, а элементы этого множества (1) называют векторами.
В линейном векторном
пространстве
можно ввести скалярное
произведение
,
поставив в соответствие каждым двум
векторам
число
.
(5)
Скалярное произведение элементов обладает следующими свойствами
1)
;
2)
;
3)
,
;
4)
,
причем
тогда и только тогда, когда
.
Число
называют длиной
вектора
.
Элементы называются ортогональными, если
.
Рассмотрим
произвольное непустое подмножество
множества
:
.
Точка
называется внутренней
точкой множества
,
если
такое, что
(т.е. каждая внутренняя точка содержится
во множестве со своей
-окрестностью).
Множество
называется открытым,
если все его точки – внутренние.
Точка
называется
точкой прикосновения множества
,
если для
,
т.е. в любой окрестности точки
содержится, хотя бы одна точка множества
.
Точка
называется предельной
точкой множества
,
если для
,
т.е. в любой окрестности точки
содержится хотя бы одна точка множества
,
отличная от
.
При этом сама точка может как принадлежать
множеству
,
так и не принадлежать ему.
Точка
называется изолированной
точкой множества
,
если для
,
т.е. существует окрестность точки
,
не содержащая никаких других точек
множества
,
кроме самой точки
.
Точка
называется граничной
точкой
,
если любая её окрестность содержит
точку, принадлежащую множеству
,
и точку, не принадлежащую множеству
.
В частности, изолированная точка является
граничной. Границей
множества
называется совокупность всех его
граничных точек; обозначение –
.
Например,
.
Все точки интервала
–
внутренние; предельными точками являются
точки отрезка
;
точки прикосновения – все точки отрезка
и
;
граничные точки –
.
Точка
также является изолированной точкой.
Множество называется
замкнутым,
если оно содержит все свои точки
прикосновения. Множество, полученное
присоединением к
всех его граничных точек называется
замыканием
множества
и обозначается
.
Множество
называется замкнутым, если
.
Множество
называется ограниченным,
если
:
,
т.е. ограниченное множество можно
заключить в шар радиуса
.
Ограниченное замкнутое множество
называется компактным.
Например, отрезок:
(6)
Точки
называются
концами отрезка,
а точки
,
в случае
,
называются внутренними
точками отрезка.
Примером замкнутого
неограниченного множества является
множество:
,
где
– фиксированное число,
–
фиксированный вектор. В случае
множество
называется
прямой
;
в
случае
– плоскостью
;
в случае
– гиперплоскостью
.
Множество называется выпуклым множеством, если отрезок, соединяющий любые две его точки, целиком содержится в этом множестве:
.
Гиперплоскости, окрестности точки, а также замкнутые полупространства
,
где
,
(7)
являются выпуклыми множествами.
Пересечение произвольного числа выпуклых множеств является выпуклым множеством.
Пусть на некотором
множестве
задана функция нескольких переменных
или, короче
,
т.е. задано правило
,
по которому каждой точке
ставится в соответствие некоторое
единственное число
(
).
Функция переменных имеющая вид
,
(8)
называется линейной функцией.
Квадратичной формой называется функция переменных
,
(9)
где
– некоторая симметричная матрица
порядка
(
).
Квадратичная
форма называется положительно
определенной
(отрицательно
определенной),
если
(соответственно
)
для любой точки
,
,
и
только при
,
т.е.
.
Например, две квадратичные формы
(a)
и (b)
являются
неотрицательными (никогда не принимают
отрицательных значений). Однако первая
является положительно определенной,
т.к. она обращается в нуль только в точке
,
а вторая не будет положительно
определенной, т.к. она обращается в нуль,
например, при
.
Квадратичная форма, принимающая как положительные, так и отрицательные значения, называется неопределенной.
Графиком функции
переменных называется множество точек
(
+1)
мерного пространства
.
Для
графиком функции является некоторая
поверхность в
.
Например, графиком линейной функции
(а) является плоскость
,
графиком функции
(б) будет параболоид
.
Поверхностью
(линией)
уровня функции
называется множество
,
где
.
(10)
Обычно поверхность
уровня имеет размерность на единицу
меньше, чем переменная
.
Если
,
то
представляют собой множество линий на
плоскости. Например, для линейной функции
(а) имеем множество параллельных прямых,
для квадратичной функции (б) линии уровня
– концентрические окружности.
Пусть функция дифференцируема в , тогда градиентом функции в точке называется вектор
.
(11)
Свойства градиента:
1. Вектор
перпендикулярен
к поверхности уровня (линии уровня) в
каждой точке.
2. Вектор
направлен в сторону возрастания функции
;
Градиентом линейной
функции
является вектор
.
Если функция дважды непрерывно дифференцируема в каждой точке области , то для неё существует симметричная матрица порядка из вторых производных
,
(12)
называемая матрицей Гессе.
Второй дифференциал функции
является квадратичной
формой с матрицей
.
Функция
определенная
на выпуклом множестве
называется выпуклой
(вогнутой)
функцией, если неравенство
.
(13)
выполнено для
любых двух точек
и любого
Если неравенство
строгое (
или
),
то функция называется строго выпуклой
(вогнутой).
Для функции одной переменной графики выпуклых и вогнутых функций обладают геометрическими свойствами:
любая точка хорды графика выпуклой (вогнутой) функции расположена не ниже (не выше) самого графика функции.
график выпуклой (вогнутой) функции расположен над (под) касательной, проведенной в любой его точке.
|
|
Строго выпуклая функция |
Строго вогнутая функция |
Если функция
дважды непрерывно дифференцируема, то
для неё можно сформулировать относительно
простой признак, по которому можно
вычислить является ли эта функция
выпуклой или вогнутой с помощью матрицы
Гессе. Функция
выпукла (вогнута) на
тогда и только тогда, когда её матрица
Гессе
неотрицательно (неположительно)
определена для
.
Если при этом матрица Гессе положительно
(отрицательно) определена для
,
то
строго выпукла (вогнута) на
(достаточное условие).
Знакоопределённость
симметричной матрицы можно установить
с помощью критерия Сильвестра. Будем
обозначать через
угловой минор
порядка
матрицы
,
т.е. минор, расположенный на пересечении
первых строк и
столбцов
.
Будем обозначать
через
главный минор
порядка
матрицы
,
т.е. минор, расположенный на пересечении
строк и
столбцов с номерами
,
.
Критерий Сильвестра:
Матрица
положительно определенная
,
;
Матрица
отрицательно определенная
,
;
Матрица
неотрицательно определенная
,
,
;
Матрица
неположительно определенная
,
,
.
Пример 1.
Исследуем на выпуклость квадратичную функцию
.
Составим матрицу Гессе
.
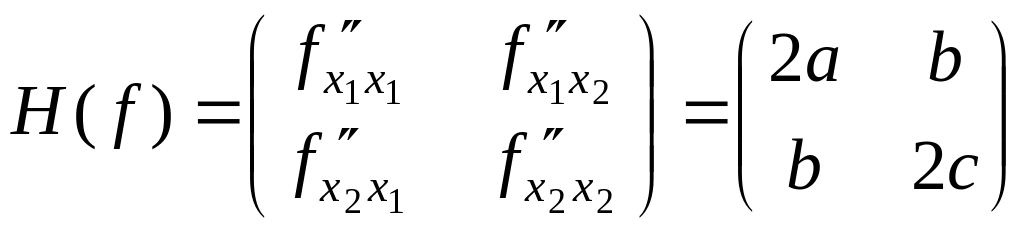Угловые миноры
,
.
Таким образом,
если
и
,
то функция
будет строго выпукла в
.
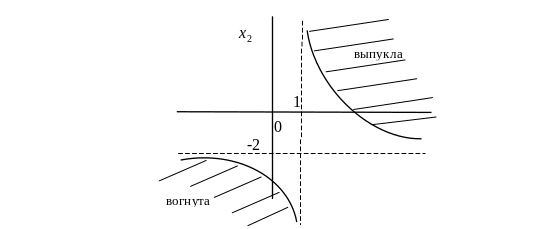
Пример 2.
Найти области выпуклости и вогнутости функции
.
Составим матрицу Гессе
,
вычислим главные миноры:
,
,
.
Функция выпукла в области, где матрица Гессе неотрицательно определена, т.е.
и вогнута в области, где матрица Гессе неположительно определена
.
Решаем неравенства
и получаем, что функция выпукла в области
и вогнута в области
.
