
- •Теория рядов. Лекция №1.
- •§1. Основные определения
- •§2. Свойства рядов
- •§3. Необходимые и достаточные условия сходимости ряда Необходимые признаки сходимости ряда
- •Достаточные признаки сходимости ряда
- •1. Признаки сравнения рядов с неотрицательными членами
- •2. Признак Даламбера.
- •3. Признаки Коши.
- •§3. Знакопеременные ряды. Знакочередующиеся ряды.
- •Абсолютная и условная сходимость рядов
- •Свойства абсолютно сходящихся рядов.
Теория рядов. Лекция №1.
Числовой ряд, сходимость, сумма. Основные свойства сходящихся рядов. Признаки сходимости числовых рядов.
Повторить: 1. понятие числовой последовательности;
2. арифметическую и геометрическую прогрессии;
3. технику вычисления пределов;
4. факториал;
5. сходимость несобственного интеграла.
§1. Основные определения
Пусть дана
последовательность
![]() ,
где индексы 1,2,3…п
показывают место членов последовательности.
,
где индексы 1,2,3…п
показывают место членов последовательности.
Определение. Сумма членов бесконечной числовой последовательности
называется рядом.
![]() (1)
(1)
При
этом числа
![]() будем называть членами
ряда, а un
– общим
членом ряда.
будем называть членами
ряда, а un
– общим
членом ряда.
Если - числа, то ряд называют числовым.
Если - функции, то ряд называют функциональным.
Определение.
Суммы
![]() ,
n
= 1, 2, …
называются
,
n
= 1, 2, …
называются
частными (частичными) суммами ряда.
Таким образом, возможно рассматривать последовательности частичных сумм ряда S1, S2, … ,Sn, …
Пример 1
Записать первые три члена ряда
![]() На практике довольно часто требуется
записать несколько членов ряда.
На практике довольно часто требуется
записать несколько членов ряда.
Сначала
![]() ,
тогда:
,
тогда:
![]() Затем
Затем
![]() ,
тогда:
,
тогда:
![]() Потом
Потом
![]() ,
тогда:
,
тогда:
![]()
Процесс можно
продолжить до бесконечности, но по
условию требовалось написать первые
три члена ряда, поэтому записываем
ответ:
![]()
Пример 2.
Записать первые
три члена ряда
![]()
подставляем
в общий член ряда
сначала
,
потом
и
.
В итоге:
![]()
Ответ оставляем
в таком виде, полученные
члены ряда лучше не упрощать,
то есть не
выполнять
действия:
![]() ,
,
![]() ,
,
![]() .
.
Ответ оставим в
виде
![]()
Пример 3.
Записать сумму в
свёрнутом виде с общим членом ряда
![]() Здесь
нет какого-то четкого алгоритма решения,
закономерность
нужно просто увидеть.
В
данном случае:
Здесь
нет какого-то четкого алгоритма решения,
закономерность
нужно просто увидеть.
В
данном случае:
![]()
Пример 4.
Записать
сумму в свёрнутом виде с общим членом
ряда
![]()
Пример 5.
Записать первые
три члена ряда
![]()
Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость. При этом возможны два случая:
Определение. Ряд называется сходящимся, если
сходится последовательность его частных сумм. Сумма
сходящегося ряда – предел последовательности его частных
сумм.
![]() (2)
(2)
Определение. Если последовательность частных сумм ряда расходится, т.е.
не имеет предела, или имеет бесконечный предел, то ряд
называется расходящимся и ему не ставят в соответствие
никакой суммы.
Хороший пример расходящегося числового ряда встретился в начале лекции:
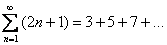 .
.
Здесь
совершенно очевидно, что каждый следующий
член ряда – больше, чем предыдущий,
поэтому
![]() и,
значит, ряд расходится. Чуть ниже мы
рассмотрим более строгий математический
критерий для данного примера.
и,
значит, ряд расходится. Чуть ниже мы
рассмотрим более строгий математический
критерий для данного примера.
В качестве примера сходящегося числового ряда можно привести
бесконечно убывающую
геометрическую прогрессию, известную
нам со школы:
![]() .
Сумму членов бесконечно убывающей
геометрической прогрессии можно найти
по формуле:
.
Сумму членов бесконечно убывающей
геометрической прогрессии можно найти
по формуле:
![]() ,
где
,
где
![]() –
первый член прогрессии,
–
первый член прогрессии,
![]() –
основание прогрессии. В данном случае:
–
основание прогрессии. В данном случае:
![]() ,
,
![]() .
Таким образом:
.
Таким образом:
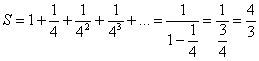 .
Получено конечное число, значит, ряд
.
Получено конечное число, значит, ряд
![]() сходится,
что и требовалось доказать.
сходится,
что и требовалось доказать.
