2.1. Система п уравнений с п неизвестными.

2.1.1. Метод обратной матрицы

Систему линейных уравнений можно записать в матричной форме, для этого введем обозначения:

- матрица коэффициентов при неизвестных;

- матрица-столбец переменных; - матрица-столбец свободных членов. Теперь систему можно записать в виде: .

Матрица называется расширенной матрицей системы уравнений.

Пусть число уравнений системы равно числу переменных, т.е. . Тогда матрица системы является квадратной, а её определитель является определителем системы.

Для получения решения системы при предположим, что квадратная матрица системы невырожденная, т.е. ее определитель . В этом случае существует обратная матрица .

Умножая слева обе части матричного равенства на матрицу , получим . Т.к. , то решением системы методом обратной матрицы будет матрица–столбец

2.1.2. Решение системы линейных уравнений по формулам Крамера.

Теорема Крамера. Пусть - определитель матрицы системы А, а - определитель матрицы, получаемой из матрицы А заменой -го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам: .

Эти формулы получили название формул Крамера.

Из рассмотрения формул ясно, что при =0 система или не имеет решения (если один из определителей ), или имеет бесчисленное множество решений при всех =0.

Заметим: 1. Если система однородна, т.е. все свободные члены равны нулю, то она всегда имеет нулевое (тривиальное) решение при ;

2. Если =0, то однородная система имеет ненулевые решения.

Существенным недостатком решения систем методом Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не применяются для решения экономических задач, сводящихся часто к системам с большим числом неизвестных.

Элементарные преобразования системы линейных уравнений, не нарушающие равносильность системы:

1. Вычеркивание уравнения системы, у которой все коэффициенты при неизвестных и свободный член равны нулю. Такое уравнение называется тривиальным.

2. Умножение обеих частей какого-либо уравнения системы на отличное от нуля число.

3. Замена -го уравнения системы уравнением, которое получается путем почленного сложения -го и -го уравнений системы.

Пример. Решим систему

методом Крамера.

Определитель данной системы

Вычислим определители , и :

.

.

.

Решение системы:

Для того чтобы убедиться в правильности решения, сделаем проверку, то есть подставим найденные значения в исходную систему

.

2.2. Решение систем линейных уравнений методом Гаусса.

Нахождение обратной матрицы через алгебраические дополнения - трудоемкий вычислительный процесс, поэтому при решении системы линейных уравнений воспользуемся численным методом, который поз­воляет с помощью элементарных преобра­зо­ваний за конечное число шагов найти решение (если оно сущест­ву­ет) и при необходимости по­лучить обратную матрицу. Этот метод называется методом полного исключения неизвестных или мето­дом Гаусса.

Пусть дана система уравнений, запишем ее расширенной матрицей

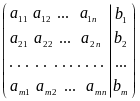
Идея метода состоит в том, чтобы с помощью элементарных преобразований свести расширенную матрицу системы к виду .

Преобразование системы состоит из ряда последовательных шагов. Условимся, что перед выполнением очередного шага в таблице вычеркиваются все строки, состоящие из одних нулей, т.е. вычеркиваются все тривиальные уравнения.

Пример. Решим систему методом Гаусса.

Начальная расширенная матрица имеет вид .

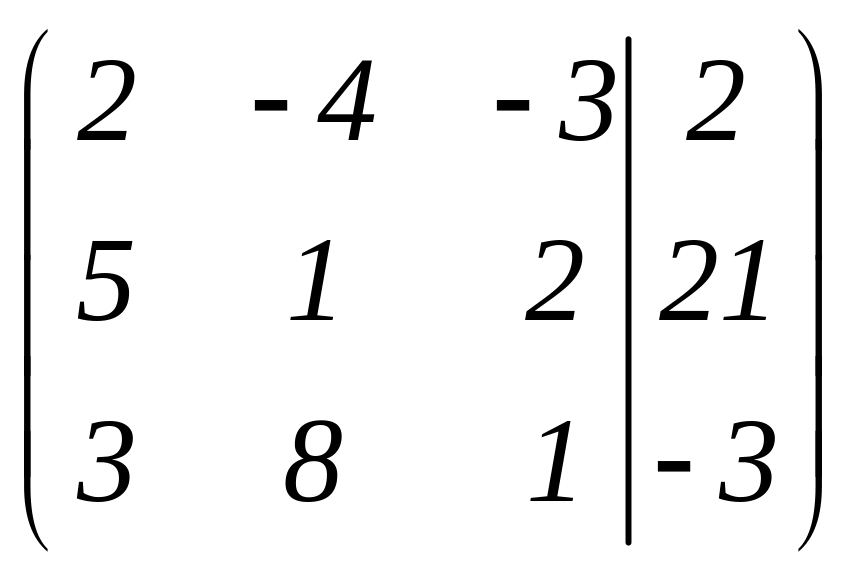Приведем ее к диагональному виду.

1-й шаг. Получим в первой строке единицу, для этого разделим первую строку матрицы на 2.

.

2-й шаг. «Обнулим» первый столбец, т.е. получим нули на месте элементов . Для этого 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:

Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда

Расширенная матрица примет вид .

В результате 1-й столбец преобразовался в .

3-й шаг. Получим 1 во второй строке, для этого делим вторую строку на 11.

.

4-й шаг. «Обнулим» второй столбец: (получим нули на месте элементов . Для этого 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда

Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на

(-14) и складываем ее с 3-й строкой, тогда

.

В результате 1-й столбец матрицы не изменился, а 2-й превратился в .

5-й шаг. Получим 1 в третьей строке. Делим 3-ю строку на :

.

6-й шаг. «Обнулим» третий столбец, для чего 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на и складываем ее с 1-й строкой, тогда

Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на и складываем ее с 2-й строкой, тогда

.

В результате 5-го и 6-го шагов 3-й столбец принял вид .

Таким образом, решение системы следующее:

Проверка: