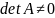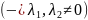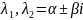- •I. Обыкновенные дифференциальные уравнения (оду)
- •Линейные уравнения. Теорема о существовании и единственности решения задачи Коши для линейного уравнения n-го порядка.
- •Линейно зависимые и линейно независимые системы функций. Определитель Вронского.
- •4. Необходимое и достаточное условие линейной независимости системы решений линейного однородного уравнения.
- •5. Фундаментальная система решений (фср) линейного однородного уравнения. Теорема о существовании фср.
- •6. Теорема о представлении общего решения линейного однородного уравнения.
- •7. Структура общего решения линейного неоднородного уравнения.
- •II. Системы оду.
- •8. Системы уравнений в нормальной форме. Задача Коши. Теорема о решения задачи Коши для системы в нормальной форме.
- •9. Линейные системы. Теорема о решения задачи Коши для линейной системы.
- •10. Линейно зависимые и линейно независимые системы вектор-функций. Определитель Вронского.
- •11. Необходимое и достаточное условие линейной независимости решений линейной од-нородной системы уравнений.
- •12. Фср для системы линейных уравнений. Теорема о существовании фср.
- •13.Теорема о представлении общего решения линейной однородной системы.
- •14.Структура общего решения линейной неоднородной системы.
- •III. Автономные систему оду
- •16. Фазовое пространство и фазовые траектории автономной системы.
- •17. Первые интегралы однородной системы. Достаточное условие первого интеграла. Теорема о существовании независимых первых интегралов.
- •18. Устойчивость по Ляпунову и асимптотическая устойчивость положения равновесия автономной системы. Условие асимптотической устойчивости положения равновесия линейной системы.
- •19. Линеризация нелинейной системы в окрестности положения равновесия. Условие асимптотической устойчивости положения равновесия нелинейной системы.
- •20. Фазовые портреты линейных однородных систем с постоянными коэффициентами на плоскости: случаи узла, седла, фокуса и центра.
- •21. Фазовые портреты нелинейных систем. Исследование положения равновесия нелинейной системы на плоскости по линейному приближению. Предельные циклы.
- •22. Фазовая плоскость оду 2-го порядка. Пример: математический маятник.
- •23. Линейные и квазилинейные учп 1-го порядка. Представление общего решения через первые интегралы системы уравнений характеристик.
18. Устойчивость по Ляпунову и асимптотическая устойчивость положения равновесия автономной системы. Условие асимптотической устойчивости положения равновесия линейной системы.
(1)
Положение равновесия (т.е. )
Начальное
условие
 (2)
(2)
Решение
задачи Коши :
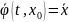
Предположение:
решение задачи (1), (2) -
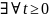 и
и
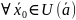 ,
где
,
где
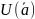 - некоторая окрестность т.
.
- некоторая окрестность т.
.
Положение
равновесия
системы (1) называется устойчивым по
Ляпунову, если
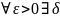 такое, что для
такое, что для
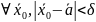 и
и
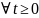 выполнено
выполнено
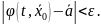
Положение
равновесия
системы (1) называется асимптотически
устойчивым по Ляпунову, если оно устойчиво
по Ляпунову, и для всех достаточно малых
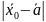 выполнено
выполнено
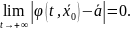
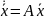 (3),
A
- постоянная (квадратная матрица). (лин.
сист.)
(3),
A
- постоянная (квадратная матрица). (лин.
сист.)
Положение
равновесия:
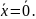
Теорема:
Положение равновесия
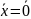 системы
(3) является асимптотически устойчивым
тогда и только тогда, когда все собственные
значения
системы
(3) является асимптотически устойчивым
тогда и только тогда, когда все собственные
значения
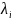 матрицы А имеют отрицательные
действительные части
матрицы А имеют отрицательные
действительные части
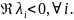 (4)
(4)
19. Линеризация нелинейной системы в окрестности положения равновесия. Условие асимптотической устойчивости положения равновесия нелинейной системы.
(1)
Предположение:
вектор функции
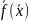 - дважды непрерывно дифференцируемая
в окрестности положения равновесия
ф-ия. По формуле Тейлора
- дважды непрерывно дифференцируемая
в окрестности положения равновесия
ф-ия. По формуле Тейлора
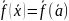 +
+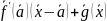 .
.
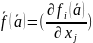 -
матрица Якоби;
-
матрица Якоби;
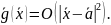
Тогда
система (1):
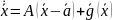 ,
где
,
где
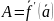 .
Положим
.
Положим
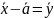 и отбросим нелинейные слагаемые.
и отбросим нелинейные слагаемые.
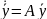 (2) - линейная система, полученная
линеризацией системы (1) в окрестности
п.р.
.
(2) - линейная система, полученная
линеризацией системы (1) в окрестности
п.р.
.
Теорема:
Если
п.р.
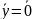 линейной системы (2) асимптотически
устойчиво, т.е. для всех собственных
значений
матрицы Якоби
выполнено условие
линейной системы (2) асимптотически
устойчиво, т.е. для всех собственных
значений
матрицы Якоби
выполнено условие
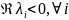 ,
то асимптотически устойчиво п.р.
.
,
то асимптотически устойчиво п.р.
.
Теорема:
Если
матрица Якоби
имеет собственное значение
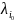 такое,
что
такое,
что
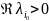 ,
то п.р.
системы (1) неустойчиво по Ляпунову.
,
то п.р.
системы (1) неустойчиво по Ляпунову.
20. Фазовые портреты линейных однородных систем с постоянными коэффициентами на плоскости: случаи узла, седла, фокуса и центра.
(1)
Точка (0,0) является положением равновесия системы (1). В зависимости от собственных значений матрицы , различают четыре типа невырожденных особых точек линейных систем: узел, седло, фокус, центр.
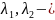 действительны
и различны
действительны
и различны
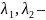 одного
знака
одного
знака
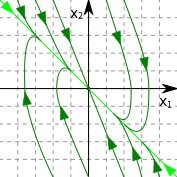
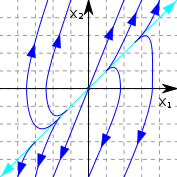
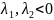 -устойчивый
-неустойчивый
-устойчивый
-неустойчивый
разного знака седло
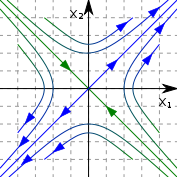
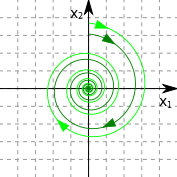

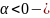 устойчивый
устойчивый
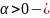 неустойчивый
неустойчивый
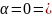 центр
центр
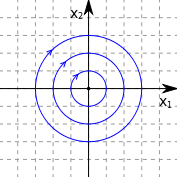
21. Фазовые портреты нелинейных систем. Исследование положения равновесия нелинейной системы на плоскости по линейному приближению. Предельные циклы.
(2)
Пусть - положение равновесия (2). Линеаризуем (2) в окрестности т. .
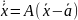 (3)
(3)
или
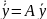 ,
где
,
где
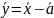
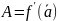 – матрица
Якоби
– матрица
Якоби
Теорема.
Пусть
собственные
значения матрицы
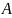 .
Если действительные части
.
Если действительные части
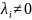 для
для
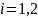 ,
то фазовые портреты линейной системы
(3) и нелинейной системы (2) в некоторой
окрестности положения равновесия
топологически эквивалентны.
,
то фазовые портреты линейной системы
(3) и нелинейной системы (2) в некоторой
окрестности положения равновесия
топологически эквивалентны.
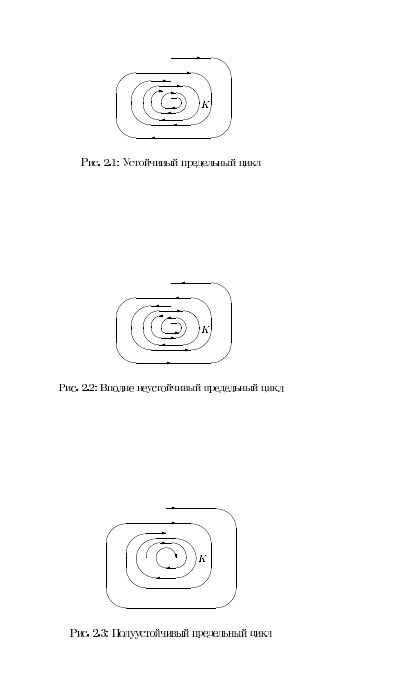
Предельные циклы
Предельным циклом системы называется изолированная замкнутая траектория P этой системы.
У
траектории P
существует окрестность, целиком
заполненная траекториями, асимптотически
приближающихся к P
при
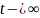 или
или
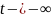 .
.