7. Структура общего решения линейного неоднородного уравнения.
Неоднородное уравнение:
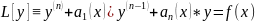(1)
Однородное уравнение:
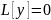(2)
Если
– фундаментальная система решений
(ФСР) однородного уравнения (2), то решение
уравнения (1) можно искать в виде:
,
где
функции
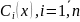подлежат определению.
II. Системы оду.
8. Системы уравнений в нормальной форме. Задача Коши. Теорема о решения задачи Коши для системы в нормальной форме.
Система ОДУ в нормальной форме:
(1)
где
,
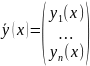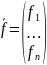
Начальное условие (НУ):
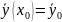(2)
где
,
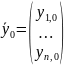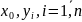– заданные числа
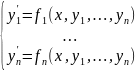(1)’
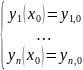(2)’
Задача Коши: найти решение системы (1), удовлетворяющее начальному условию (2).
Теорема:
Пусть функции
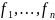и их производные
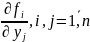непрерывны в некоторой области
.
Тогда для
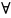точки
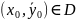решение задачи Коши (1)(2)
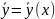существует и единственно в некоторой
окрестности точки
.
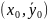9. Линейные системы. Теорема о решения задачи Коши для линейной системы.
Линейная система:
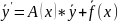(1)
где
,
,
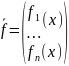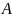– квадратная матрица порядка
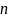
Начальное условие (НУ):
(2)
где , – заданные числа
Задача Коши: найти решение системы (1), удовлетворяющее начальному условию (2).
Теорема:
Пусть
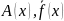непрерывны на интервале
.
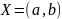Тогда для
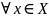и
решение задачи Коши (1)(2) существует и
единственно на
.
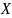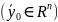
10. Линейно зависимые и линейно независимые системы вектор-функций. Определитель Вронского.
Вектор
функции
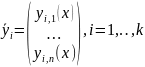- называется линейно
зависимыми,
если существуют числа
,
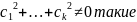такие что
,
что
.
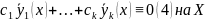Если (4) возможно только при
,
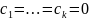то
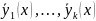- линейно
независимы.
Пусть
k=n.
Тогда (4)
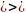
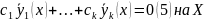
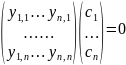(5’)
Определитель Вронского:
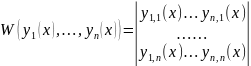
11. Необходимое и достаточное условие линейной независимости решений линейной од-нородной системы уравнений.
Теорема.
Решения
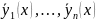однородной системы
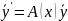линейно независимы на
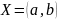
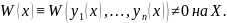
Доказательство:
Пусть
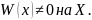Тогда в силу леммы ( если существует
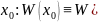то
– линейно независимы) следует
– линейно независимы.Пусть решения – линейно независимы
.
Тогда пусть (от противного) существует
.
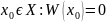Тогда система
при
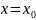имеет ненулевое решение
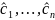.Рассмотрим функцию
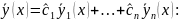
а)
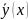решение системы
б)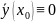
По
теореме существования единственности
это решение совпадает с решением
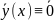, т.е.
,
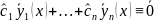т.е.
- линейно зависимы – это противоречие!!!
=>
.
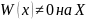Следствие:
Если
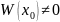в
некоторой точке
,
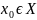то решения
– линейно независимы и
.
12. Фср для системы линейных уравнений. Теорема о существовании фср.
Любые n линейно независимые решения системы называются фундаментальной системой решений (ФСР).
Теорема. ФСР существует.
Доказательство:
Пусть
существует единственная матрица порядка
n,
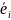- её столбцы. Пусть
– некоторая точка. Найдем решение
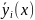системы
с начальными условиями:
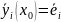(сущ. по Т
),
т.е.
=>
- линейно независимы, т.е. образуют ФСР
системы.
13.Теорема о представлении общего решения линейной однородной системы.
Tеорема
: Общее
решение системы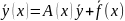
(1) имеет вид :
,
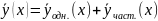где
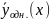– общее решение однородного уравнения
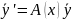(2),
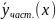– частное
решение однородной системы.
Док-во:
Пусть – некоторое решение системы (1).
Замена:
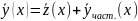
Система
(1):
,):
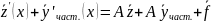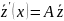–однородная
система (2) =>
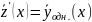–общее
решение однородной системы, ч.т.д.,
т.е.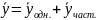
ч.т.д.