I. Обыкновенные дифференциальные уравнения (оду)

1. ОДУ n-го порядка в нормальной форме. Задача Коши. Теорема о существовании и единственности решения задачи Коши.

ОДУ – уравнение вида , где F – заданная функция, х – независимая переменная, у(х)- искомая функция, - ее производная, n –порядок уравнения. Функция у(х) называется решением, если при подстановке ее в уравнение, уравнение обращается в тождество.

Теорема. - (уравнение первного порядка, разрешенная относительно производной) (1)

Начальное условие: y(x0)= (2)

заданная точка.

Задача Коши: Найти решение уравнения (1), удовлетворяющее НУ (2).

Теорема!.

Пусть функция f(x,y) непрерывную в некоторой области и имеет в этой области непрерывную производную . Тогда для любой точки решение задачи Коши (1), (2) существует и единственно в некоторой окрестности .

2. Линейные уравнения. Теорема о существовании и единственности решения задачи Коши для линейного уравнения n-го порядка.

НУ: (4)

Предположение. Коэф. 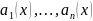и правая часть непрерывны на некотором интервале (a,b).

Теорема. При сделанных предположениях решение задачи Коши (5), (4) существует и единственно для .

3. Линейно зависимые и линейно независимые системы функций. Определитель Вронского.

Опр.: Система функций

К (4)

Если равенство (4) возможно только при то система функций называется линейно независимой.

Определитель Вронского.

4. Необходимое и достаточное условие линейной независимости системы решений линейного однородного уравнения.

Решение y₁(x),…, y_n(x) уравнения L(y)=0 линейно независимо тогда и только тогда, когда на Х.

Док-во:

1) Если 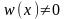на Х, то функции y₁(x),…, y_n(x) линейно независимы.

2) Пусть y₁(x),…, y_n(x) линейно независимы. Предположим (от противного), что : , тогда система (*)

при x=x₀ имеет нетривиальное решение ,

Рассмотрим функцию . Она является решением уравнения L(y)=0 (в силу леммы), удовлетворяющим условиям (в силу (*)) при x=x_0.

Тем же условиям удовлетворяет решение . По теореме о ! , эти решения совпадают: на Х. Т.е. функции y₁(x),…, y_n(x) линейно зависимы (противоречие). Отсюда ни в какой точке интервала.

5. Фундаментальная система решений (фср) линейного однородного уравнения. Теорема о существовании фср.

Любые n линейно независимых решений y₁(x),…, y_n(x) уравнения L(y)=0 называются ФСР этого уравнения.

Теорема. ФСР уравнения L(y)=0 существует.

Док-во:

Пусть Е – единичная матрица n*n, e_i, i=1,…, n – её столбцы.

Для каждого i=1,…, n найдем решение y_i(x) уравнения L(y)=0, удовлетворяющее условиям = e_i , где – произвольная точка.

По теореме о ! эти решения существуют.

6. Теорема о представлении общего решения линейного однородного уравнения.

Общим решением линейного однородного уравнения L(y)=0 является линейная комбинация

(*)

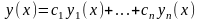n линейно независимых частных решений этого уравнения y₁(x),…, y_n(x).

Док-во:

То, что функция y(x), определяемая формулой (*), является решением уравнения L(y)=0, следует из леммы о том, что линейная комбинация является решением однородного уравнения. Теперь покажем, что любое решение уравнения L(y)=0 представимо в виде линейной комбинации функций y₁,…, y_n. Для некоторой фиксированной точки рассмотрим систему линейных уравнений:

(**)

Определителем этой системы является определитель Вронского для функций y₁,…, y_n в точке x₀, который в силу их линейной независимости не равен 0. Значит система (**) имеет единственное решение .

Тогда функция удовлетворяет тем же начальным условиям, что и функция (*). В силу единственности решения задачи Коши имеем , т.е. – линейная комбинация функций y₁,…, y_n, ч. и т.д.