2. Задание

2.1. Теоретическая часть

1. Дать определение следующим понятиям: момент силы, момент инер­ции, угловое ускорение (Что характеризует каждая из величин, как определяется её численное значение , каково её направление, если величина векторная?). Пояснить на рисунке смысл использованных буквенных обозначений.

2. Сформулировать II закон Ньютона для вращательного движения (словами

и аналитически) . Изобразить графически характер зависимости углового

ускорения от действующего момента сил (при постоянном моменте

инерции) и от момента инерции (при постоянном моменте сил).

3.Каким образом в работе предлагается проверить спра­ведливость основного уравнения динамики вращательного движения?

4. Какими способами на маятнике Обербека можно изменить момент силы ?

5. Какими способами на маятнике Обербека можно изменить момент инерции системы?

6. Вывести рабочие формулы для определения углового ускорения и момента силы натяжения нити.

2.2. Экспериментальная часть

1. Установить грузики на спицах маятника Обербека в положение, указанное преподавателем, и сбалансировать маятник.

(Почему необходима балансировка?).

2. Привести систему во вращение с помощью грузика m, подвешенно­го к нити, и измерить:

а) высоту опускания грузика;

б) время опускания грузика (не менее трех раз);

в) радиус шкива, на котором намотана нить.

3. Повторить измерения по п.2., изменяя массу грузика так, чтобы получилось не менее 4-х экспериментальных точек. Все данные занести в таблицу.

4. Вычислить угловое ускорение и момент силы в каждом из 4 ва­риантов опыта по формулам (1.5) и (1.6).

5. Нанести экспериментальные точки на график зависимости между и М.

6. Проверить выполнимость основного закона динамики вращательно­го движения одним из методов, описанных в тексте (по указанию преподавателя).

ЛАБОРАТОРНАЯ РАБОТА № 209

ОПРЕДЕЛЕНИЕ ГОРИЗОНТАЛЬНОЙ СОСТАВЛЯЮЩЕЙ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ

ПРИБОРЫ И ОБОРУДОВАНИЕ: блок питания, сменный модуль, магазин сопротивления, измерительный прибор.

1.Теория метода

Земля - естественный магнит, магнитное поле которого, как полагают современные теории, обусловлено, в основном токами, текущими по поверхности ядра Земли и частично намагниченностью горных пород Земли.

Магнитное поле невидимо, но его можно обнаружить с помощью магнитной стрелки (или пробного контура с током).

Для наглядного представления магнитных полей используют линии напряженности (индукции) - линии, касательные к которым в каждой точке совпадают с вектором напряженности.

Магнитное поле Земли представлено на рис. 1. Северный магнитный полюс N - в нынешнюю геологическую эпоху располагается вблизи южного географического S, а южный магнитный S - вблизи северного географического n.

Рис. 1

Наибольшее практическое значение имеет горизонтальная составляющая вектора напряженности магнитного поля Земли ,направление которой принимается за направление магнитного меридиана.

Для определения горизонтальной составляющей воспользуемся

методом сравнения с искусственным магнитным полем , созданным электрическим током, текущем по проводнику и направленным перпендикулярно .

Пусть магнитный меридиан MN располагается в плоскости чертежа, как показано на рис. 2. Направление горизонтальной составляющей в точке А нам покажет магнитная стрелка, помещенная в эту точку (положение 1 рис. 2). Создадим в этой точке искусственное поле . Поля по принципу суперпозиции складываются геометрически: _. Магнитная стрелка повернется на угол и установится вдоль результирующего поля рез (положение 2, рис. 2).

Рис. 2

Из геометрии рис. 2 , отсюда

. (1)

Искусственное поле создается с помощью электрического тока, текущего по кольцевым проводникам (колеца Гельмгольца), которые представляют собой две одинаковые катушки (содержащие одинаковое число проволочных витков ), расположенные симметрично оси магнитной стрелки компаса (рис. 5), поэтому

, (2)

где - напряженность магнитного поля катушки;

- число витков в катушке;

- напряженность магнитного поля, создаваемого проволочным витком.

Напряженность магнитного поля витка вычисляется на основании принципа суперпозиции и закона Био-Савара-Лапласа.

В соответствии с принципом суперпозиции напряженность магнитного поля на оси витка в точке А равна геометрической сумме напряженностей полей , создаваемых элементами витка в этой точке

. (3)

В соответствии с законом Био-Савара-Лапласа

.

Построив векторы от всех элементов тока (по правилу векторного произведения) замечаем, что они образуют коническую поверхность (рис. 3)

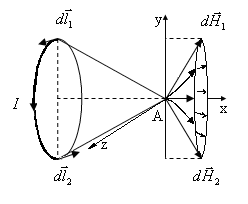
Рис. 3

Для определения модуля напряженности Н_В запишем уравнение (3) в проекциях на оси х, у, z:

и найдем .

Для любой пары диаметрально противоположных элементов (например dl₁ и dl₂) проекции векторов и на ось у равны по абсолютной величине и имеют противоположные знаки, поэтому в сумме дают ноль, тогда =0. Аналогично для проекций на ось z: =0.

Проекции же на ось х для всех векторов имеют одинаковые знаки, тогда

H_B= . (4)

На основании закона Био-Савара-Лапласа модуль найдется, как

,

А его проекция на ось х:

, (5)

где α – угол между и ; α=90; sinα=1;

β – угол между и осью х (рис.4), β одинаков для всех элементов тока

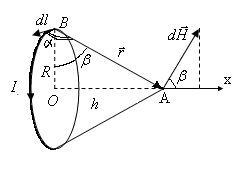
Рис. 4

Подставляя (5) в (4), получим

, (6)

где R – радиус витка.

В треугольнике ОВА В=β, ;

С учетом этих соотношений для модуля напряженности поля, созданного одним витком, по которому течет ток I, получаем:

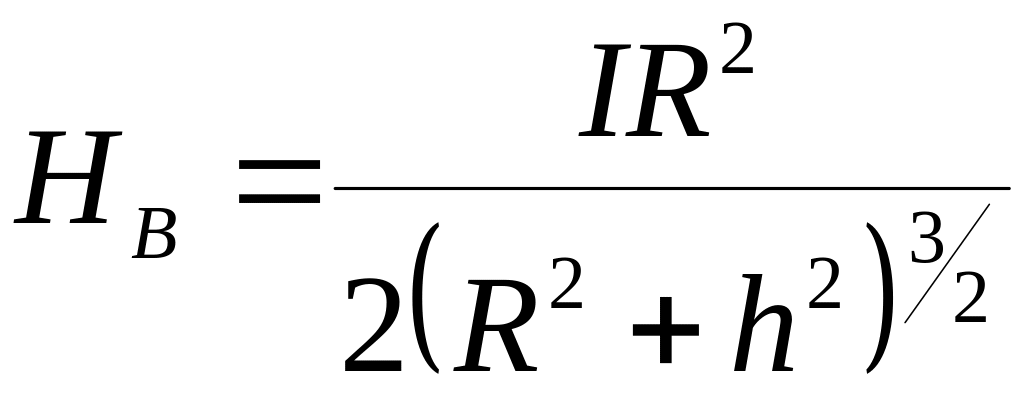. (7)

Так как в каждой катушке n витков, а токи в катушках направлены так, что их магнитные поля усиливают друг друга

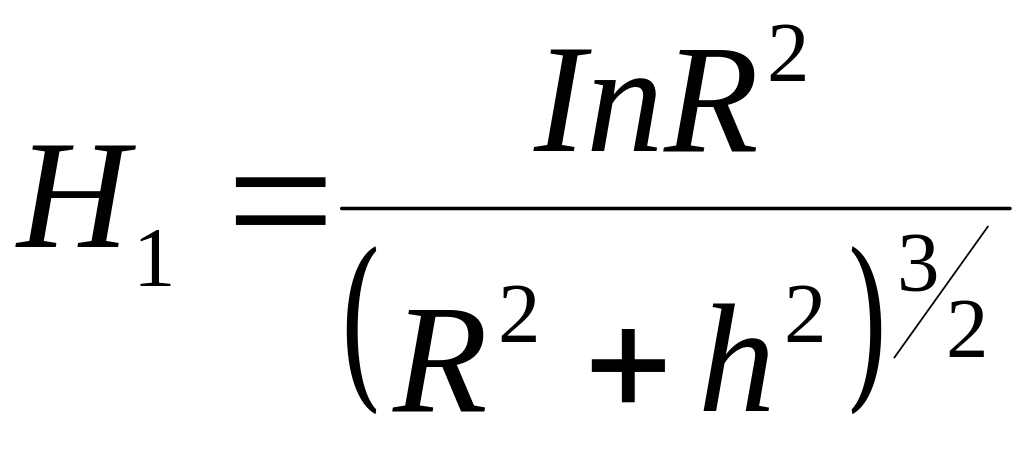. (8)

Подставляя это выражение в (1), окончательно получаем рабочую формулу для определения горизонтальной составляющей поля Земли

. (9)