4.1.3 Процесс дросселирования.

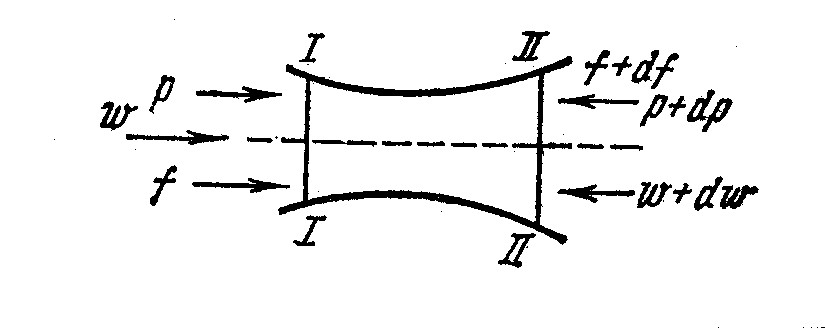
Адиабатное расширение газа от одного давления р₁ до другого постоянного давления р₂ без совершения внешней работы называется д р о с с е л и р о в а н и е м. Суть процесса заключается в проходе потока вещества через какое-то препятствие – дроссельный вентиль, заслонку и калиброванное отверстие. Если рассмотреть поток перед и за препятствием на некотором расстоянии, то можно заключить, что в первом сечении совершается работа при входе, а во втором сечении работа при выходе. Сумма этих работ с точностью до кинетической энергии потока равна : -p₁v₁ + p₂ v₂. Тогда согласно первому закону термодинамики:

При отсутствии теплообмена с внешней средой (Q=0) имеем:

или i₁=i₂=const (4.15)

Вывод выражения (4.15) не сопровождался какими-то предположениями о свойствах вещества, поэтому оно справедливо и для идеального и для реальных газов. При дросселировании энтальпия рабочего тела не меняется. Для идеального газа внутренняя энергия не зависит от объема и в процессе дросселирования имеет место равенство работ : p₁v₁=p₂ v₂ , что соответствует уравнению изотермы. Температура при дросселировании идеального газа не меняется.

Для реальных газов в зависимости от протекания кривых i =const дросселирование сопровождается изменением температуры. Величина называется дифференциальным эффектом Джоуля – Томсона.

Учитывая, что в процессе дроселирования имеется конечный перепад давлений, запишем:

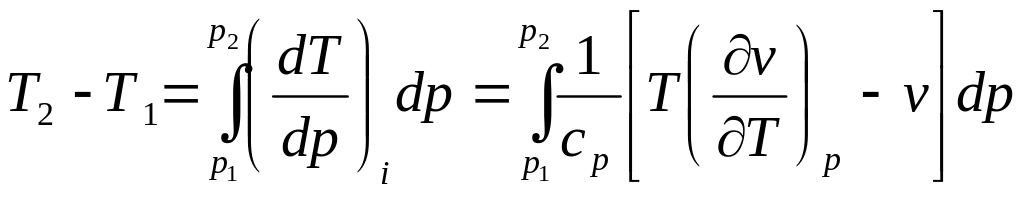(4.16)

Это выражение определяет так называемый интегральный эффект Джоуля-Томсона (изменение температуры при конечной разности давлений). В инженерных расчетах уравнение (4.16) решается с помощью S-T диаграммы (рис.4.16).

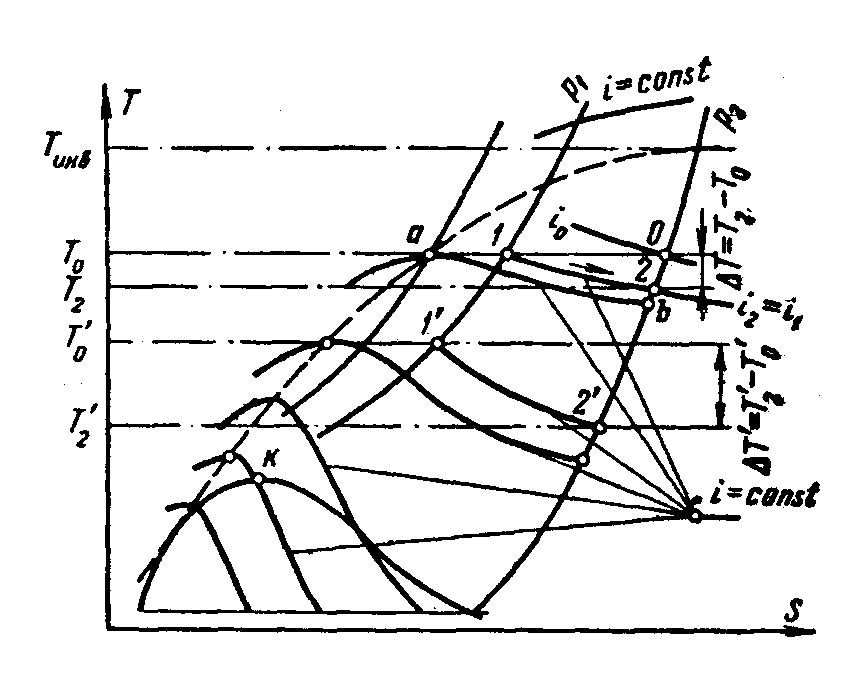
Рис. 4.16. Процесс дросселирования в T-S координатах

Из анализа уравнения (4.16) и рис.4.16 можно видеть, что знак изменения температуры может быть как положительным, так и отрицательным. Изменение знака дроссель-эффекта называют инверсией. Кривая инверсии разграничивает области положительного (охлаждение) и отрицательного (нагревание) дроссель эффекта.

Ориентировочные значения инверсии получаются с использованием безразмерной формы записи уравнения состояния веществ.

Уравнение кривой инверсии в относительных (приведенных) величинах для газа, подчиняющегося уравнению ван-дер- Ваальса, имеет вид:

(4.17)

или

(4.18)

Здесь

- относительная температура

- относительное давление

График кривой, описанной уравнением (4.18), приведен на рисунке 4.17.

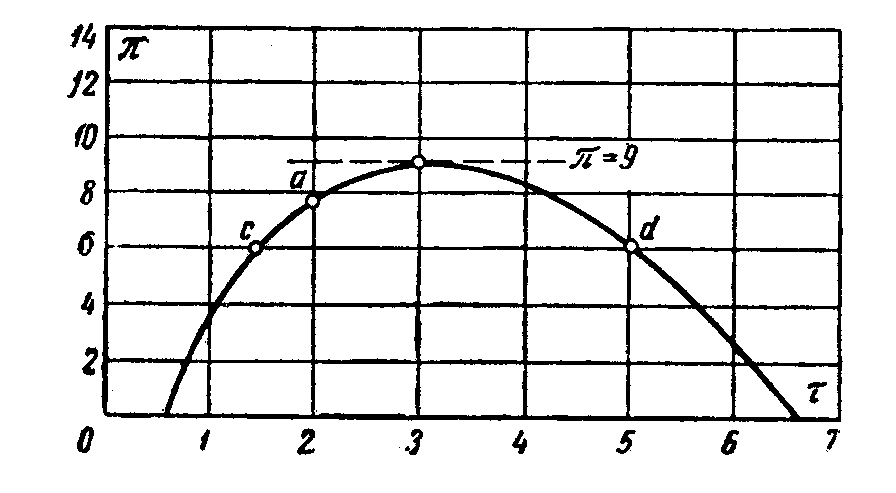
Рис. 4.17. Кривая инверсии в приведенных координатах

Область внутри зтой кривой соотвествует положительному дроссель – эффекту. Если фиксировать температуру (τ = const), и изменять давление, то имеет место одно значение точки инверсии. Если фиксировать относительное давление, то наблюдается две точки инверсии с и d . Доказано экспериментально существование точки инверсии в области пара, а другой – в области жидкости. Из графика рис.4.17 видно, что имеется максимальная температура, при которой возможен положительный дроссель-эффект, он равен 6,75. На рис.4.16 пунктиром нанесена кривая, проходящая через экстремальные значения изоэнтальп, которая асимптотически приближается к максимальному значению.

В области малых плотностей и высоких температур Джоулем и Томсоном получена простая зависимость для дроссельного эффекта:

(4.19)

Можно получить простую связь двух эффектов понижения температур

и

(4.20)

Здесь означает дифференциальный эффект снижения температуры при отборе энергии (расширение в турбинах, которое предполагается по адиабате).

Если сравнивать процессы снижения температур веществ путем отбора работы в турбинах (детандерах) с процессом дросселирования, то можно сделать следующие выводы.

1. Величина эффекта снижения температуры отбором работы существенно положительная в областях состояний, физически допускающих расширение.

2. С увеличением температуры эффект снижения температуры отбором работы возрастает, при этом увеличивается и сама полезная работа.

3. С увеличением давлений, т.е при уменьшении удельных объемов, эффект понижения температур отбором работы снижается.

4. В окрестности критических состояний и в области состояний кипящей жидкости величины и 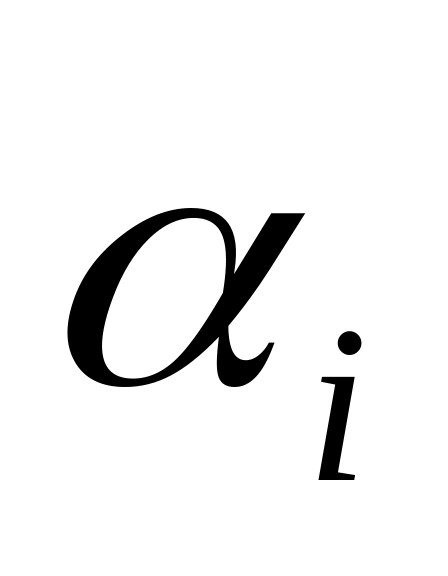наиболее близки друг к другу, и в этом случае более сложное устройство в виде детандера может быть заменено простым дроссельным вентилем.

Истечение газов и паров.

Уравнение энергии в механическом виде, называемое уравнением Бернулли, приведе-

но при рассмотрении первого закона термодинамики.

При выводе этого уравнения не учитывалось влияние гравитационных сил и при рассмотрении истечения газа считалось, что газом не совершается так называемая техническая работа.

Изменение кинетической энергии рабочего тела может происходить как в трубах постоянного сечения, так и в специально спрофилированных каналах переменного сечения, называемых соплами и диффузорами.

Если при перемещении газа по каналу происходит его расширение с уменьшением давления и увеличением скорости, то такой канал называют соплом.

Если в канале происходит торможение потока с увеличением статического давления,то такой канал называют диффузором.

Основным условием при истечении является сохранение постоянства потока массы рабочего тела по сечениям или уравнение неразрывности струи

, (а)

где f₁, f₂, _... f – площади поперечного сечения канала;

с₁, с₂, ...с – скорости течения рабочего тела;

v₁, v₂, ...,v – удельные объемы.

Течение газа по каналу полагаем без подвода и отвода теплоты, т.е. адиабатное.

В каждом поперечном сечении канала скорость с , давление р, температура Т и другие параметры тела постоянны по сечению канала, т.е. имеют во всех точках плоскости, перпендикулярной к оси трубы, одинаковое значение (осредненные величины).

Рассматривается установившееся движение, называемое стационарным. При этом величины скоростей, давления, температур и удельных объемов могут меняться по длине канала от сечения к сечению, но не зависят от времени. Все величины являются функцией одной координаты – длины канала.