XIV.Розширення поняття числа.

Множина дійсних чисел, її властивості і геометрична інтерпретація.

Завдання вчителя математики початкових класів – ввести дитину в світ цифр і чисел.

Ми в математиці користуємося десятковою системою числення:

0,1,2,3,4,5,6,7,8,9.

Ці цифри ми запозичили в арабів. Серед них є 5 парних (0,2,4,6,8) і 5 непарних (1,3,5,7,9). Усі парні числа можна об’єднати у формулу:

2п, якщо п = 0,1,2,3…

Усі непарні числа можна записати такою формулою:

2п – 1, якщо п = 0,1,2,3…

Спочатку я ввожу дітей в світ чисел від 1 до 10, потім від 1 до 100, і так до +&. Отже множина натуральних чисел є

N = 1,2,3,4,5…

0 – не входить в множину натуральних чисел.

Розширяємо кругозір учня з математики, до натуральних чисел включаємо цілі від’ємні числа. Утворюється множина цілих чисел

Z = N + цілі від’мні + 0

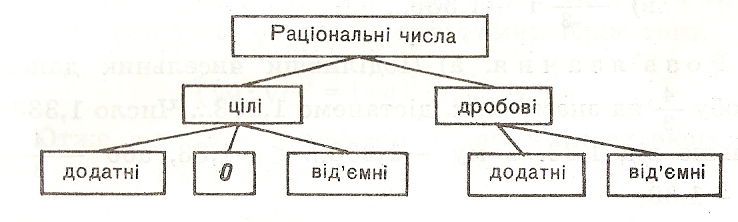
Додаючи до цілих чисел дробові (додатні і від’ємні) одержуємо множину раціональних чисел.

Q= Z + дробові (додатні і від’ємні)

Відомі вам досі числа – цілі і дробові, додатні і від’ємні – становлять множину раціональних чисел. Раціональними їх називають тому, що кожне з них можна записати у вигляді частки двох цілих чисел, а слово «частка» латинською мовою – ratio.

XV.Поняття функції.

Пряма пропорційність, її властивості і графік.

Якщо дві змінні величини зв’язані між собою так, що кожному значенню однієї з них відповідає єдине значення іншої, то кажуть, що між цими змінними існує функціональна залежність.

Прямою пропорційність називається функція, яку можна задати формулою виду у = кх, де х – незалежна змінна, к – число, що дорівнює нулю. Графіком прямої пропорційності є пряма, яка проходить через початок координат.

Обернена пропорційність, її властивості і графік.

Залежність між змінними х і у, яку можна задати формулою у = , де к – деяке стале число, називають оберненою пропорційністю.

Графіком оберненої пропорційності є крива лінія, що складається із двох віток, розміщених в першому і третьому координатних кутах при к  0, або в другому і четвертому – при к  0. Ця лінія називається рівносторонньою гіперболою.

Графік функції симетричний відносно початку координат, тому що функція непарна. Ця функція необмежена. Якщо х  0 і х  0 і к  0 , то функція спадна.

Якщо к  0 , то функція зростаюча.

Xvі. Поняття числового виразу та його значення. Вираз зі змінною.

Числовий вираз і його значення.

Богданович М.В.Математика : Підруч. для 2 кл. – К.: Освіта, 2002.- 160 с.

с. 71, №383

Записи виду : 25 + 3, 60 – 20, 10 + 4 – 8, 16 – (9-5) називаються числовими виразами. Якщо виконаємо дії, то знайдемо значення виразів : 28 – значення першого виразу, 40 – другого, 6 – третього і 12 четвертого. Запис 25 + 3 = 28 можна читати так : сума чисел 25 і 3 дорівнює 28, або значення виразу 25 + 3 дорівнює 28.

Мета – виховувати математичну мову учнів.

Вираз зі змінною, його область визначення.

Областю визначення виразу зі змінною називається множина допустимих значень цієї змінної.

Богданович М.В. Математика : Підруч. для 3 кл.- К.: Освіта, 2003.-160 с.

с. 42, №258

Розглянь розв'язання двох задач, кожна з яких містить буквене дане.

1) 3 однієї грядки зібрали 6 гарбузів, а з другої — а гарбузів. Усі гарбузи поклали в 2 ящики, порівну в кожний. Скільки гарбузів поклали в один ящик?

6 + а — зібрали всього гарбузів;

(6 + а) : 2 — поклали гарбузів в один ящик.

Відповідь: (6 + а) : 2 гарбузів.

2) 3 однієї грядки зібрали к гарбузів, а з другої — в 3 рази більше. Усі гарбузи поклали в 2 ящики, порівну в кожний. Скільки гарбузів поклали в один ящик?

К  3 — зібрали гарбузів з другої грядки; к + к  3 — зібрали гарбузів з двох грядок; (к + к-3) : 2 — поклали гарбузів в один ящик. Відповідь: (к + к  3) : 2 гарбузів.

Якщо умова задачі містить буквене дане, то відповідь записують у вигляді виразу.

Мета – розвивати математичну мову учнів.

Тотожні перетворення виразів зі змінною.

Заміна одного виразу іншим, тотожно рівним йому, називається тотожним перетворенням виразу.

Наприклад : х + 2х + 5х = 8х.

Мета : розвивати математичну мову.

Тотожність.

Рівність, правильна при всіх допустимих значеннях букв, що виходять із неї, називається тотожністю. Властивості математичних дій є тотожності.

Мета : розвивати математичну мову.