
- •Учебный модуль №10 «ряды» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Ряды» «Важные сведения из пределов»
- •Ряды «эталоны»
- •Знакопеременные ряды
- •Степенные ряды
- •Ряд Фурье
- •10.1. Числовые ряды. Сходимость и сумма ряда
- •10.2. Простейшие свойства числовых рядов
- •10.3. Необходимое условие сходимости ряда. Гармонический ряд
- •10.4. Ряды с положительными членами. Теоремы сравнения
- •10.5. Признаки Даламбера и Коши
- •10.6. Знакочередующиеся ряды. Признак Лейбница
- •10.7. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды
- •10.8. Функциональные ряды. Область сходимости
- •10.9. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенных рядов
- •10.10. Интегрирование и дифференцирование степенных рядов
- •10.11. Ряды Тейлора и Маклорена. Условия разложения функции в ряд Тейлора
- •10.12. Разложение по степеням х функций
- •10.13. Приложение рядов к приближенным вычислениям
- •10.14. Ряды Фурье. Коэффициенты Фурье
- •10.15. Разложение в ряд Фурье четных и нечетных функций
- •10.16. Разложение в ряд Фурье функций, заданных на
- •10.17. О разложении в ряд Фурье непериодических функций
- •Вопросы к экзамену по модулю №10
10.5. Признаки Даламбера и Коши
Рассмотрим еще три достаточных признака для исследования числовых рядов с положительными членами.
Теорема 10.5.1 (признак Даламбера). Если в ряде
отношение (n+1)-го члена к n-му при n имеет конечный предел
 ,
,
то 1) ряд сходится, если р < 1;
2) ряд расходится, если р > 1.
(В случае р = 1 ответа на вопрос о сходимости или расходимости ряда теорема не дает, нужны дополнительные исследования.)
Доказательство.
1) Пусть р < 1. Рассмотрим число q, удовлетворяющее соотношению р < q < 1.
Из определения
предела следует, что
![]() ,
что для всех
,
что для всех
![]() будет иметь место
будет иметь место


 .
Запишем это неравенство для различных
значений n,
начиная с номера N.
.
Запишем это неравенство для различных
значений n,
начиная с номера N.

Рассмотрим теперь три ряда
![]() (исходный ряд)
(исходный ряд)
![]()
![]()
Ряд есть сумма геометрической прогрессии с q < 1, следовательно, он сходится. Члены ряда меньше соответствующих членов ряда ввиду выполнения неравенств , поэтому он сходится.
Но ряд получается добавлением к сходящемуся ряду конечного числа членов (N 1), поэтому он тоже сходится.
2) Пусть р
> 1. Тогда
из равенства
 (где р >
1) следует, что, начиная с некоторого
номера N,
т.е. для
(где р >
1) следует, что, начиная с некоторого
номера N,
т.е. для
![]()
 .
.
![]() для всех
.
Но это означает, что члены ряда возрастают,
начиная с номера N
+1, и поэтому
общий член ряда не стремится к нулю.
Следовательно, ряд расходится.
для всех
.
Но это означает, что члены ряда возрастают,
начиная с номера N
+1, и поэтому
общий член ряда не стремится к нулю.
Следовательно, ряд расходится.
Замечание
10.5.1. Ряд
будет расходиться и в том случае, когда
р =
.
Это следует из того, что если
 ,
то, начиная с некоторого номера n
= N,
будет иметь место неравенство
,
то, начиная с некоторого номера n
= N,
будет иметь место неравенство
 ,
или
,
или
![]()
![]() .
.
Пример 10.5.1. Исследовать сходимость ряда
![]()
Решение. Здесь
![]() ,
,
 .
Следовательно,
.
Следовательно,

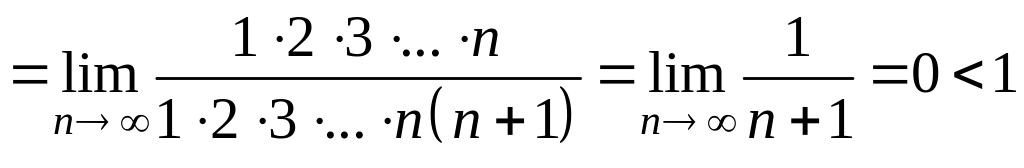 .
Ряд сходится.
.
Ряд сходится.
Пример
10.5.2. Исследовать
сходимость ряда
![]() .
.
Решение.  .
Ряд расходится.
.
Ряд расходится.
Замечание
10.5.2. Если
р =
1, но отношение
![]() для всех номеров n,
начиная с некоторого, больше единицы,
то ряд расходится. Это следует из того,
что если
>1,
то
для всех номеров n,
начиная с некоторого, больше единицы,
то ряд расходится. Это следует из того,
что если
>1,
то
![]() и общий член не стремится к нулю, когда
n
.
и общий член не стремится к нулю, когда
n
.
Пример 10.5.3. Исследовать сходимость ряда
![]()
Решение.
 .
.
В данном случае
ряд расходится, так как
![]() >1
для всех п:
>1
для всех п:
 .
.
Теорема
10.5.2 (радикальный
признак Коши). Если для ряда с положительными
членами
существует конечный предел
![]() ,
то
,
то
если р < 1, ряд сходится;
если р > 1, ряд расходится.
Как и в признаке Даламбера, случай р = 1 требует дополнительного исследования.
Доказательство практически ничем не отличается от доказательства теоремы 10.5.1, поэтому его приводить не будем.
Пример 10.5.4. Исследовать сходимость ряда

Решение. Применим радикальный признак Коши:
 .
Ряд сходится.
.
Ряд сходится.
Теорема
10.5.3 (интегральный
признак Коши). Пусть члены ряда
имеют вид
![]() ,
где f(x)
– неотрицательная монотонно убывающая
функция на промежутке
,
где f(x)
– неотрицательная монотонно убывающая
функция на промежутке
![]() ,
а
1.. Тогда ряд
сходится (расходится) тогда и только
тогда, когда сходится (расходится)
несобственный интеграл
,
а
1.. Тогда ряд
сходится (расходится) тогда и только
тогда, когда сходится (расходится)
несобственный интеграл
 .
.
Пример
10.5.5. Исследовать
на сходимость ряд
 .
.
Решение. Положим
![]() .
Функция f(x)
непрерывна и монотонно убывает на
.
Функция f(x)
непрерывна и монотонно убывает на
![]() .
Так как несобственный интеграл
.
Так как несобственный интеграл
 ,
,
т.е. расходится, то в соответствии с интегральным признаком Коши расходится и заданный ряд.
Пример 10.5.6. Исследовать на сходимость обобщенный гармонический ряд . Эта функция удовлетворяет всем условиям теоремы 10.5.3. Рассмотрим несобственный интеграл
 .
.
Рассмотрим три случая:
пусть р > 1 р-1 > 0, тогда
 ,
т.е
,
т.е
интеграл конечен и, следовательно, ряд сходится.
пусть р < 1 1-р > 0 и
 ,
т.е.
,
т.е.
интеграл расходится и, следовательно, ряд расходится.
если р = 1, рассматриваем
 ,
ряд расходится.
,
ряд расходится.
Таким образом, ряд Дирихле сходится, если р > 1, и расходится, если р 1.
Заметим, что ни признак Даламбера, ни радикальный признак Коши не решают вопрос о сходимости этого ряда, так как соответствующие пределы равны 1.
Обобщенный гармонический ряд (ряд Дирихле), а также ряд, составленный из членов геометрической прогрессии, часто используются как «эталонные» ряды при применении обоих признаков сравнения.
