
- •Учебный модуль №10 «ряды» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Ряды» «Важные сведения из пределов»
- •Ряды «эталоны»
- •Знакопеременные ряды
- •Степенные ряды
- •Ряд Фурье
- •10.1. Числовые ряды. Сходимость и сумма ряда
- •10.2. Простейшие свойства числовых рядов
- •10.3. Необходимое условие сходимости ряда. Гармонический ряд
- •10.4. Ряды с положительными членами. Теоремы сравнения
- •10.5. Признаки Даламбера и Коши
- •10.6. Знакочередующиеся ряды. Признак Лейбница
- •10.7. Знакопеременные ряды. Абсолютно и условно сходящиеся ряды
- •10.8. Функциональные ряды. Область сходимости
- •10.9. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенных рядов
- •10.10. Интегрирование и дифференцирование степенных рядов
- •10.11. Ряды Тейлора и Маклорена. Условия разложения функции в ряд Тейлора
- •10.12. Разложение по степеням х функций
- •10.13. Приложение рядов к приближенным вычислениям
- •10.14. Ряды Фурье. Коэффициенты Фурье
- •10.15. Разложение в ряд Фурье четных и нечетных функций
- •10.16. Разложение в ряд Фурье функций, заданных на
- •10.17. О разложении в ряд Фурье непериодических функций
- •Вопросы к экзамену по модулю №10
10.15. Разложение в ряд Фурье четных и нечетных функций
Пусть f(x)
четная 2-периодическая
функция. Тогда
![]() является нечетной, а
является нечетной, а
![]()
четной функцией. Следовательно,
четной функцией. Следовательно,
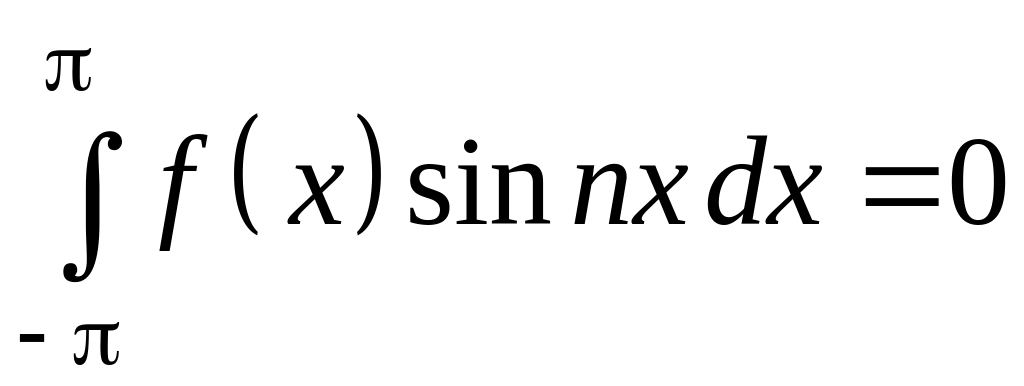 ,
,
 .
Согласно формулам
для коэффициентов ряда Фурье получаем
.
Согласно формулам
для коэффициентов ряда Фурье получаем
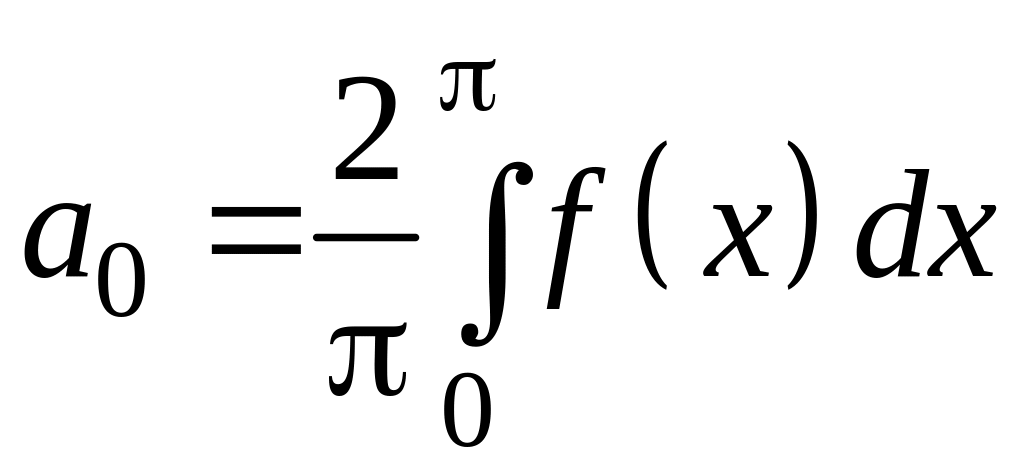 ,
,
 ,
bn
= 0,
,
bn
= 0,
т.е. ряд Фурье для четной функции имеет вид
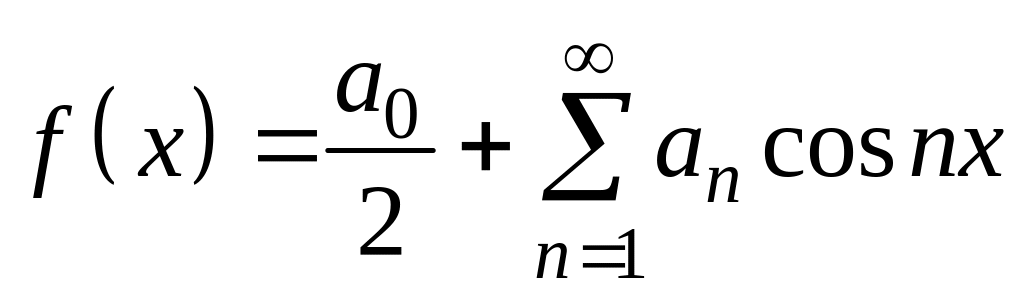 .
.
Аналогично, если
f(x)
нечетная 2-периодическая
функция, то
![]()
нечетная, а
нечетная, а
![]()
четная функция. В этом случае имеем:
четная функция. В этом случае имеем:
а0
= 0, аn
= 0, 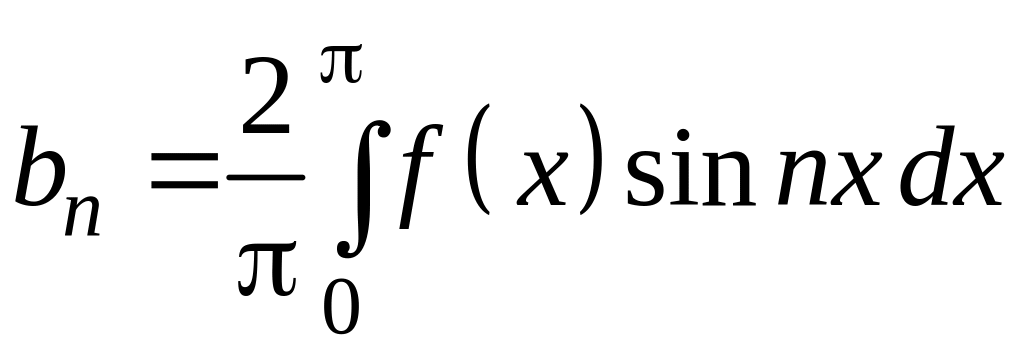 ,
,
а ряд Фурье для нечетной функции имеет вид
 .
.
Таким образом, четная 2-периодическая функция разлагается в ряд Фурье только по косинусам, а нечетная 2-периодическая функция раскладывается в ряд Фурье только по синусам.
Пример
10.15.1. Разложить в ряд Фурье 2-периодическую
функцию
![]() ,
заданную на [,
].
,
заданную на [,
].
Решение. Функция четная, поэтому bn = 0.
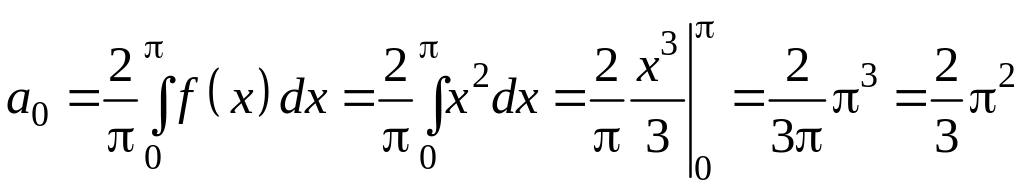 .
.



![]() .
Значит, ряд Фурье данной функции имеет
вид
.
Значит, ряд Фурье данной функции имеет
вид
 .
.
Так как функция кусочно-монотонна, ограничена и непрерывна, то это равенство выполняется во всех точках.
Полагая х = в этом равенстве, получим
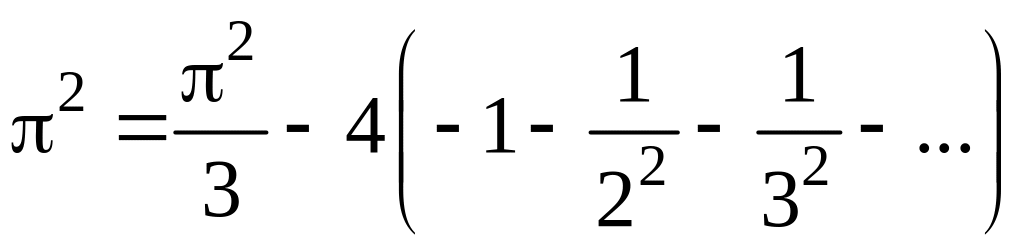

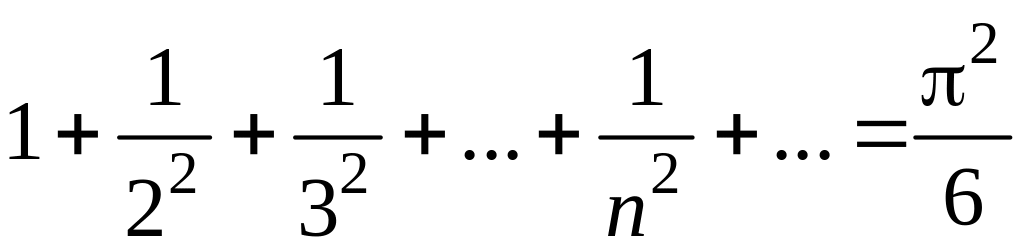 .
Мы нашли сумму обобщенного гармонического
ряда для р
= 2,
.
Мы нашли сумму обобщенного гармонического
ряда для р
= 2,
 .
.
Полагая х
= 0, получаем:

10.16. Разложение в ряд Фурье функций, заданных на
Пусть f(x)
есть периодическая функция с периодом
![]() ,
вообще говоря, отличным от 2.
Разложим ее в ряд Фурье.
,
вообще говоря, отличным от 2.
Разложим ее в ряд Фурье.
Сделаем замену переменной по формуле
![]() .
.
Тогда функция
 будет периодической функцией от t
с периодом 2.
Действительно,
будет периодической функцией от t
с периодом 2.
Действительно,
 .
.
Ее можно разложить в ряд Фурье на [-p, p]:
 ,
,
где
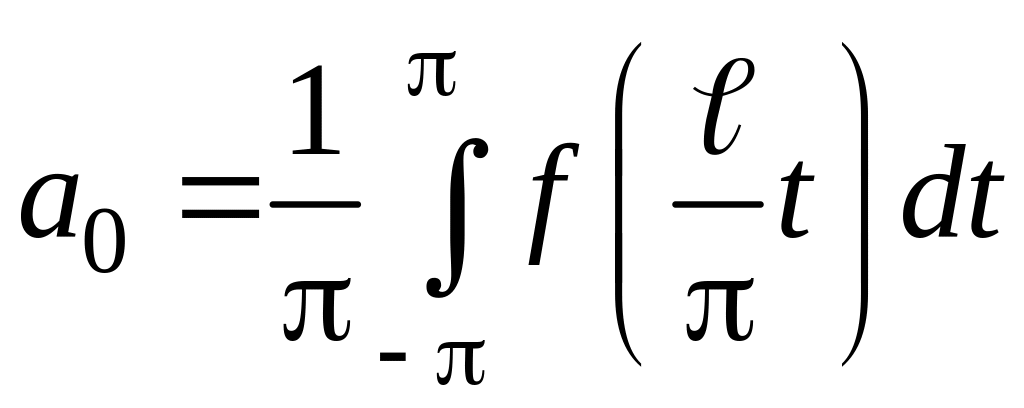 ,
,
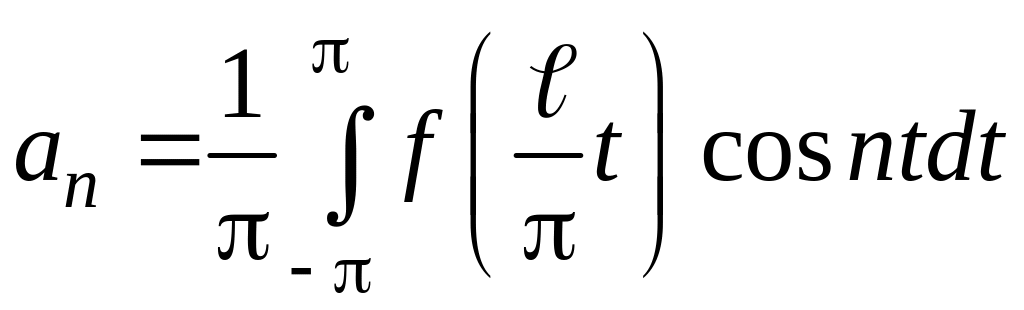 ,
, 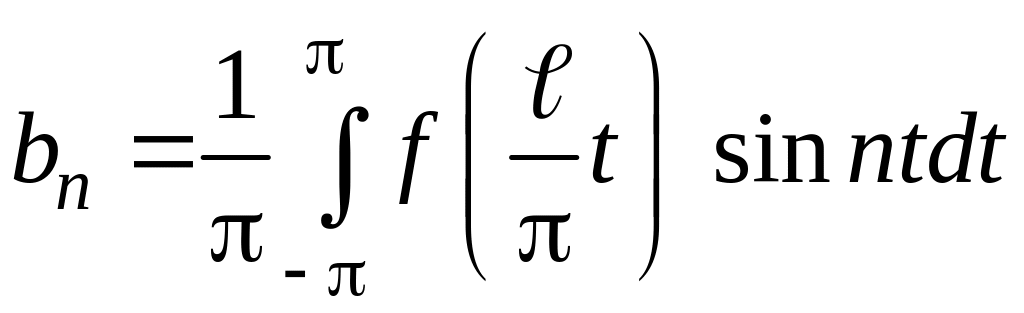 .
.
Вернемся теперь к старой переменной х:
,
![]() ,
, ![]() .
.
Тогда будем иметь
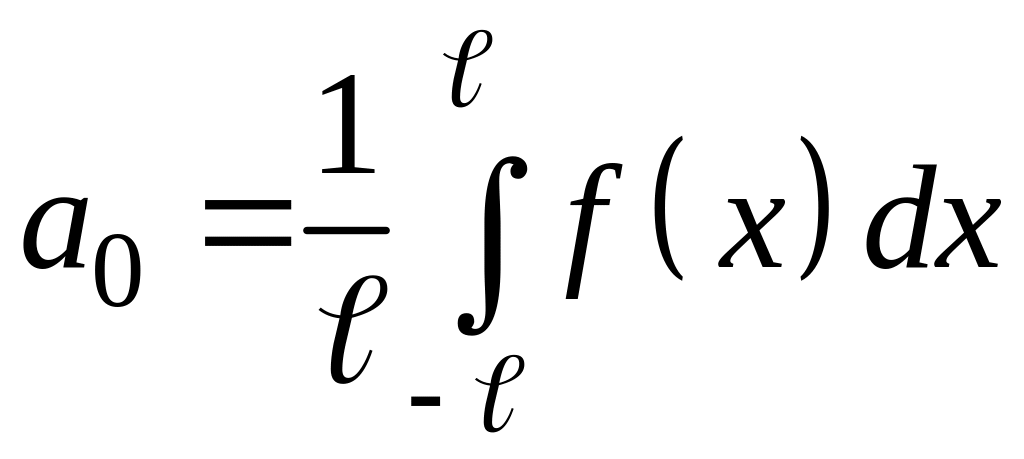 ,
, 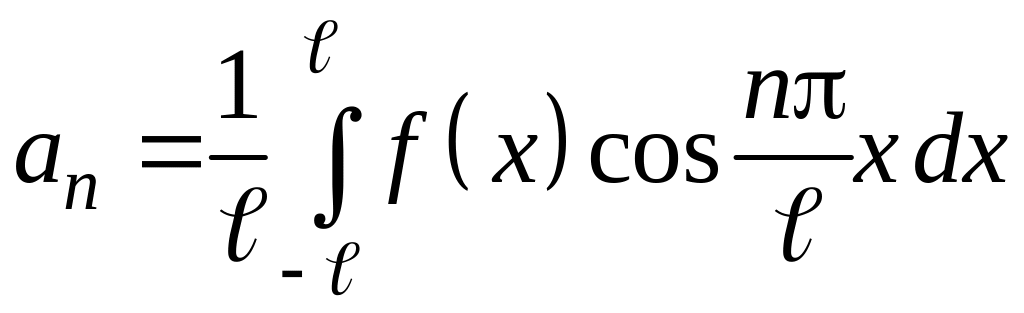 ,
, 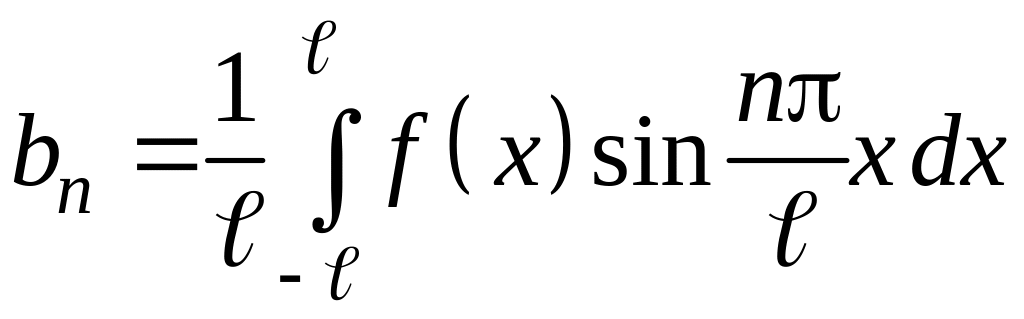 ,
,
а формула примет вид
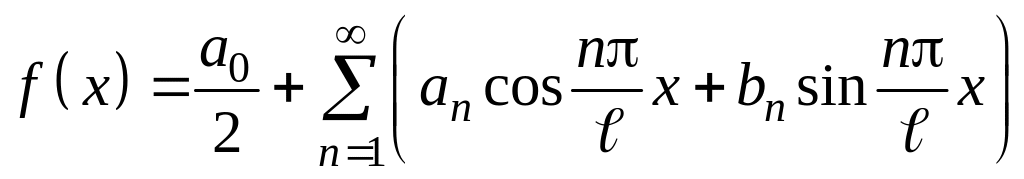 .
.
Если f(x) четная функция, то
bn
= 0, 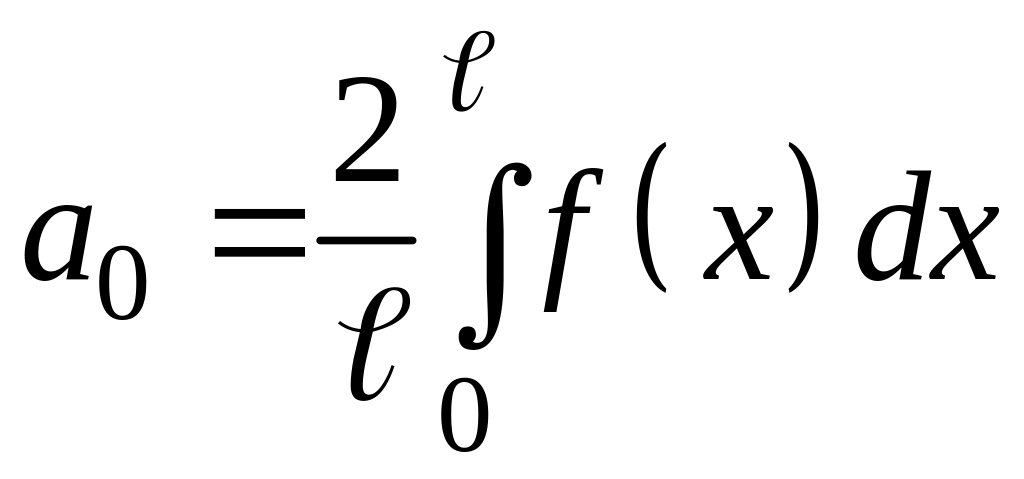 ,
,
 ;
;
если же f(x) нечетная функция, то
а0
= 0, аn
= 0, 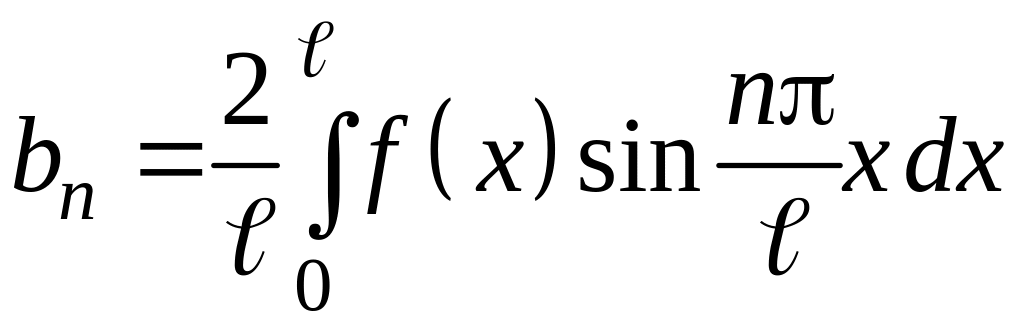 .
.
Пример
10.16.1. Разложить в ряд Фурье периодическую
функцию f(x)
с периодом
,
которая на
![]() задается равенством
задается равенством
![]() .
.
Решение. Все условия теоремы Дирихле выполняются. Так как функция четная, то bn = 0,
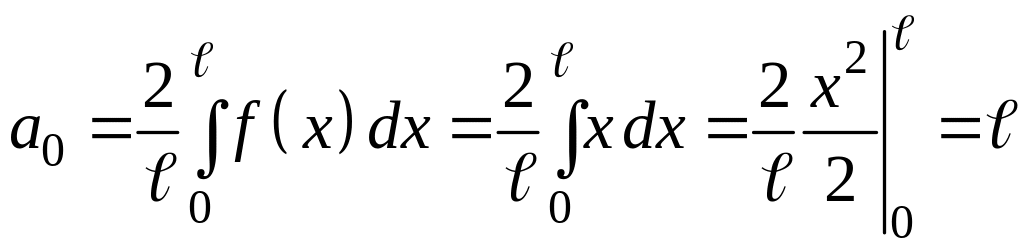 ,
,
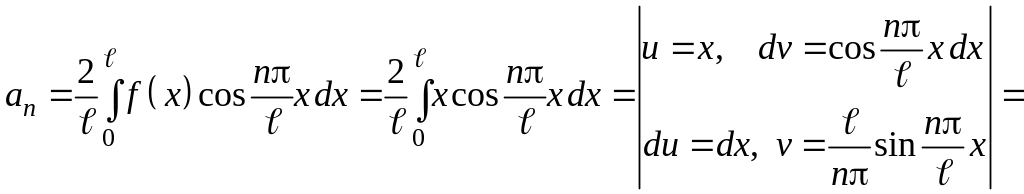

 .
.
Следовательно,
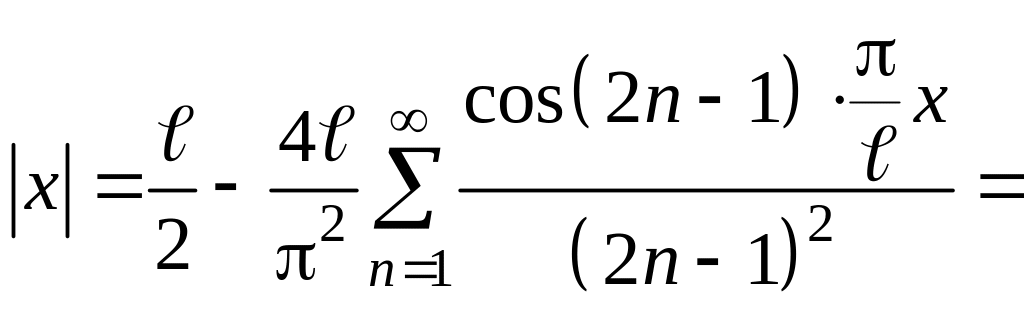
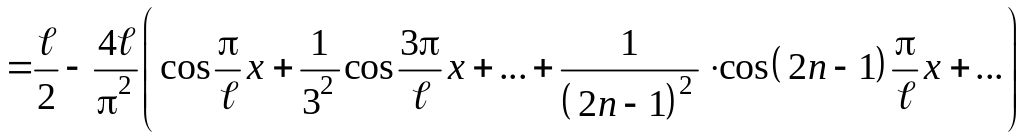 .
.
Пусть х
= 0,

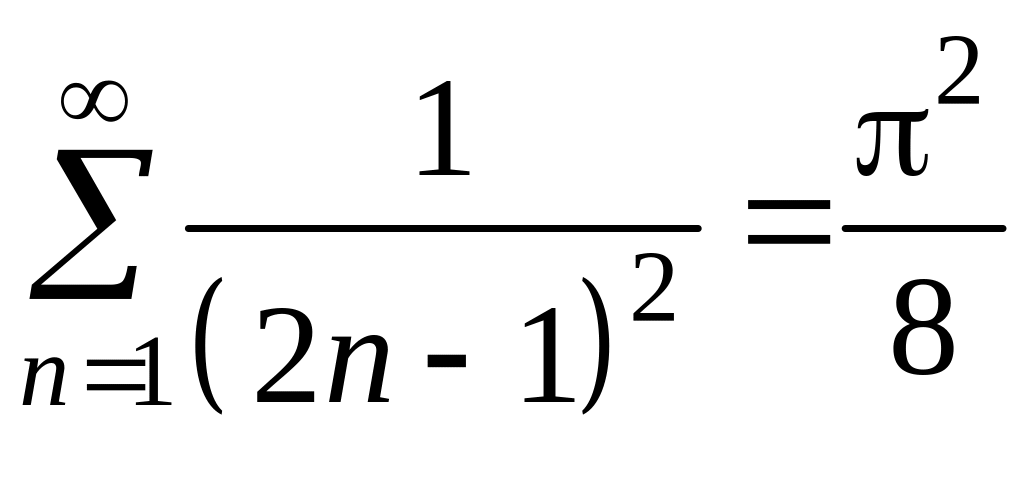 .
.
10.17. О разложении в ряд Фурье непериодических функций
Пусть функция f(x) задана на [0, p]. Чтобы разложить f(x) на этом отрезке в ряд Фурье, доопределим ее на отрезке [p, 0]. В результате получим функцию, заданную на всем отрезке [p, p], которую уже можно разложить в ряд Фурье. Ясно, что получившийся ряд будет зависеть от характера продолжения первоначальной функции на [p, 0]. Рассмотрим два возможных случая.
Если продолжить (доопределить) f(x) четным образом с отрезка [0, p] на отрезок [p, 0] (рис.10.17.1), то получим четную функцию, которая, как известно, раскладывается в ряд Фурье только по косинусам.
А
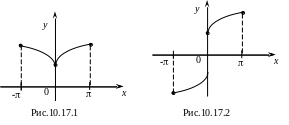 налогично,
продолжая f(x)
нечетным образом с отрезка [0, p]
на отрезок [p,
0] (рис.10.17.2), то получим нечетную функцию,
разлагающуюся в ряд Фурье только по
синусам.
налогично,
продолжая f(x)
нечетным образом с отрезка [0, p]
на отрезок [p,
0] (рис.10.17.2), то получим нечетную функцию,
разлагающуюся в ряд Фурье только по
синусам.
