
- •9.16. Линейные однородные дифференциальные уравнения
- •I. Основные понятия теории дифференциальных уравнений.
- •III. Линейные дифференциальные уравнения первого порядка
- •Учебный модуль №9 «Дифференциальные уравнения» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Дифференциальные уравнения»
- •9.1. Физические задачи, приводящие к дифференциальным уравнениям
- •9.2. Основные понятия теории дифференциальных уравнений
- •9.3. Дифференциальные уравнения первого порядка. Задача Коши
- •9.4. Дифференциальные уравнения с разделенными и разделяющимися переменными
- •9.5. Однородные дифференциальные уравнения и приводящиеся к ним
- •9.6. Линейные дифференциальные уравнения первого порядка
- •9.7. Уравнение Бернулли
- •9.8. Дифференциальные уравнения в полных дифференциалах
- •9.9. Особые решения дифференциальных уравнений первого порядка
- •9.10. Модели прикладных задач с применением дифференциальных уравнений
- •9.11. Дифференциальные уравнения высших порядков. Задача Коши. Понятие общего и частного решений
- •9.12. Дифференциальные уравнения, допускающие понижение порядка
- •9.13. Понятие о краевых задачах для обыкновенных дифференциальных уравнений
- •9.14. Линейные дифференциальные уравнения высших порядков
- •9.15. Линейные однородные дифференциальные уравнения, свойства их решений. Определитель Вронского. Условия линейной зависимости и независимости решений
- •9.16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •9.17. Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных
- •9.18. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •9.19. Системы дифференциальных уравнений. Решение систем дифференциальных уравнений с постоянными коэффициентами
- •Вопросы к экзамену по модулю №9
- •Дифференциальные уравнения в полных дифференциалах.
9.11. Дифференциальные уравнения высших порядков. Задача Коши. Понятие общего и частного решений
Уравнение вида
![]() ,
где n
> 1, называется
дифференциальным
уравнением n-го
порядка.
Уравнение
,
где n
> 1, называется
дифференциальным
уравнением n-го
порядка.
Уравнение
![]()
называется
уравнением n-го
порядка, разрешенным относительно
старшей производной
![]() .
Всякому решению дифференциального
уравнения n-го
порядка (как и уравнению первого порядка)
на плоскости XOY
соответствует интегральная кривая.
Общее решение дифференциального
уравнения n-го
порядка зависит от n
произвольных
постоянных С1,
С2,
…, Cn.
Оно имеет вид
.
Всякому решению дифференциального
уравнения n-го
порядка (как и уравнению первого порядка)
на плоскости XOY
соответствует интегральная кривая.
Общее решение дифференциального
уравнения n-го
порядка зависит от n
произвольных
постоянных С1,
С2,
…, Cn.
Оно имеет вид
![]() ,
где
- n
раз дифференцируемая функция. Если
решение дифференциального уравнения
n-го
порядка удается получить в неявном виде
,
где
- n
раз дифференцируемая функция. Если
решение дифференциального уравнения
n-го
порядка удается получить в неявном виде
![]() ,
,
то оно называется общим интегралом этого уравнения.
Геометрически общее решение (или общий интеграл) дифференциального уравнения n-го порядка представляет собой семейство интегральных кривых на плоскости XOY, зависящее от n параметров С1, С2, …, Cn. Для выделения конкретного (частного) решения из общего необходимо иметь, помимо дифференциального уравнения, некоторые дополнительные условия, позволяющие определить значения произвольных постоянных С1, С2, …, Cn. Одним из таких условий является задание значений неизвестной функции и ее первых n1 производных в некоторой точке x0 интервала (a, b), на котором определено решение уравнения:
![]() ,
,
где
![]() – заданные числа. Условия называются
начальными
условиями
или условиями
Коши.
– заданные числа. Условия называются
начальными
условиями
или условиями
Коши.
Задача отыскания частного решения уравнения n-го порядка, удовлетворяющего начальным условиям , называется задачей Коши для этого уравнения.
Теорема
9.11.1 (о
существовании и единственности решения
задачи Коши). Пусть дано уравнение и
начальные условия . Если функция
![]() непрерывна в окрестности точки
непрерывна в окрестности точки
![]() и имеет непрерывные производные
и имеет непрерывные производные
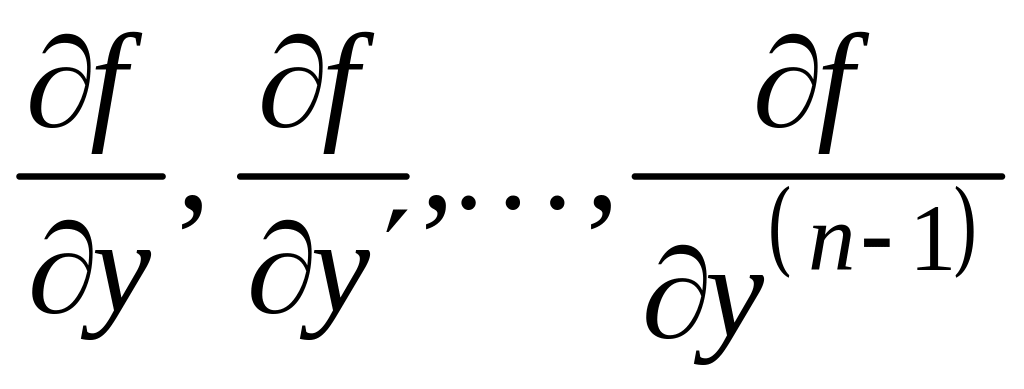 ,
то существует единственное решение
уравнения, определенное в некотором
интервале (a,
b),
содержащем точку x0,
и удовлетворяющее заданным начальным
условиям.
,
то существует единственное решение
уравнения, определенное в некотором
интервале (a,
b),
содержащем точку x0,
и удовлетворяющее заданным начальным
условиям.
9.12. Дифференциальные уравнения, допускающие понижение порядка
Задача интегрирования дифференциальных уравнений высших порядков является значительно более сложной, чем задача интегрирования дифференциальных уравнений первого порядка. Одним из основных методов (для некоторых частных видов) интегрирования дифференциальных уравнений высших порядков является понижение порядка уравнения, т.е. сведение его с помощью соответствующей замены к уравнению более низкого порядка.
Рассмотрим некоторые виды дифференциальных уравнений, допускающих понижение порядка.
Уравнение вида
![]() .
.
Порядок этого уравнения понижается всякий раз на единицу путем последовательного интегрирования:
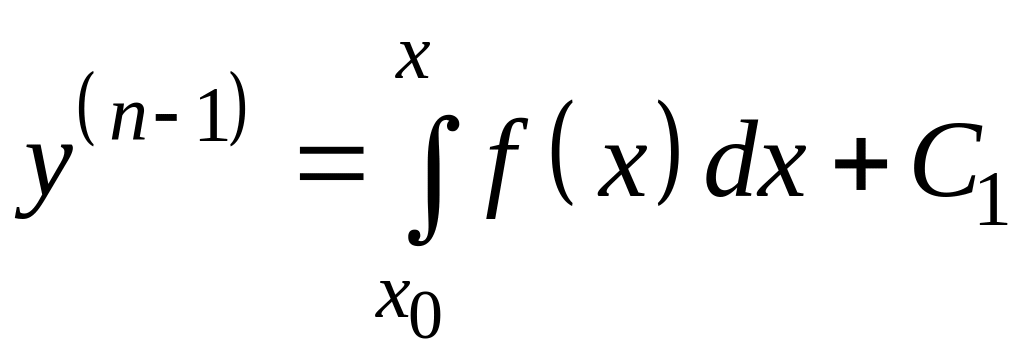 ,
,
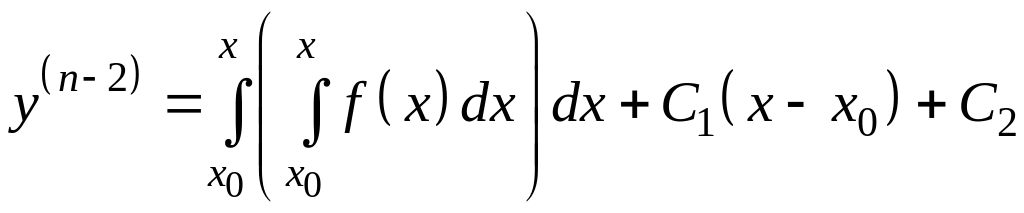 ,
,
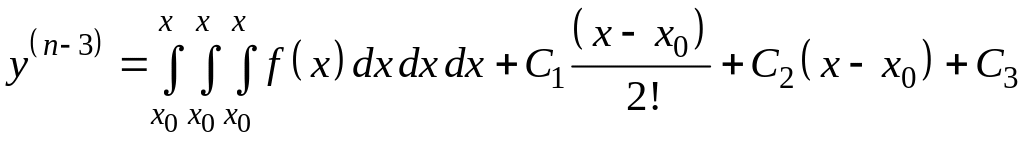 ,
,
………………………………………………………………
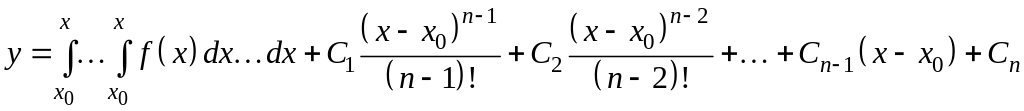
Запись общего
решения в виде определенного интеграла
позволяет легко решить задачу Коши по
заданным начальным условиям
,
![]() .
Подставляя эти условия снизу вверх,
получим (так как
.
Подставляя эти условия снизу вверх,
получим (так как
![]() ):
):
![]() ,
, ![]() , …,
, …, ![]() .
.
Пример
9.12.1. Найти
частное решение уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]() ,
,
![]() ,
,
![]() .
.
Решение. Так
как х0
= 0,
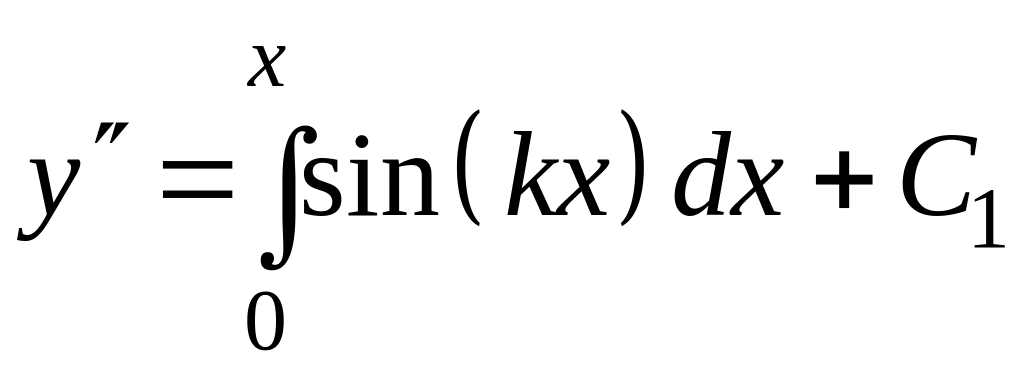
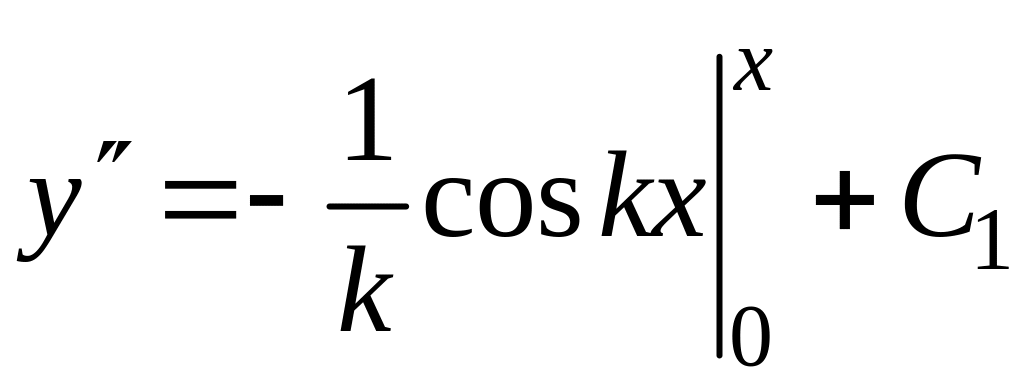
![]() .
Подставляем начальное условие
.
.
Подставляем начальное условие
.
![]()
С1=2,
т.е.
С1=2,
т.е.
![]()
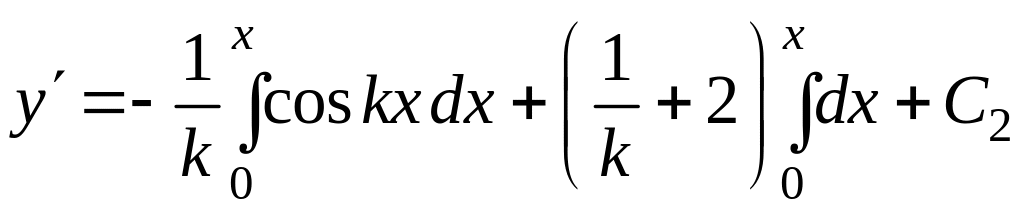
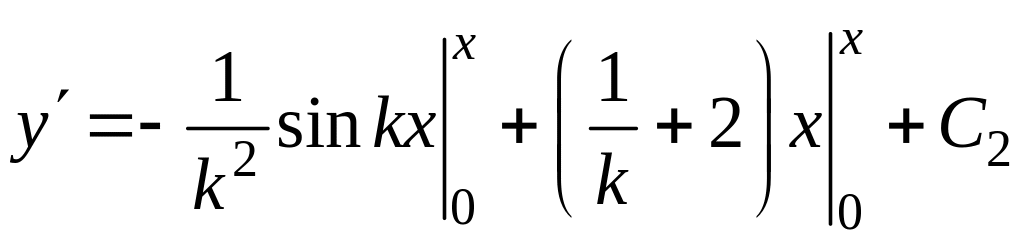 ,
т.е.
,
т.е. 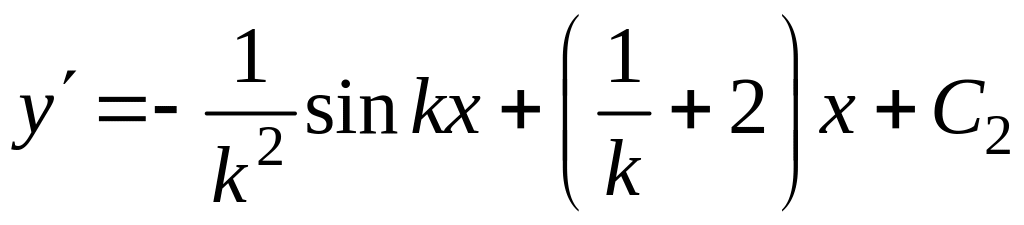
1=С2
(т.к.
).
И, наконец,
1=С2
(т.к.
).
И, наконец,
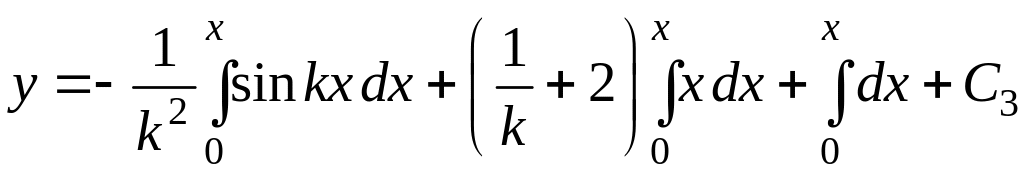
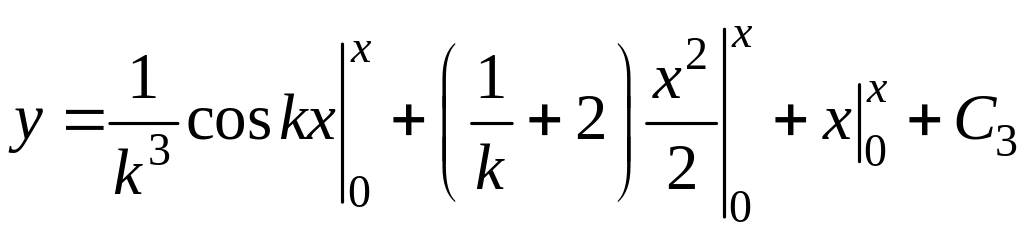
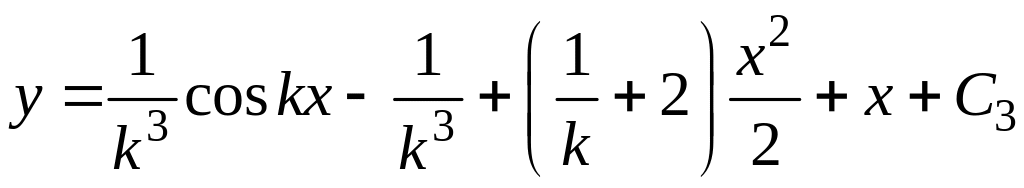 .
Подставляя последнее начальное условие
,
получаем 0 = С3.
Таким образом, искомое частное решение
.
Подставляя последнее начальное условие
,
получаем 0 = С3.
Таким образом, искомое частное решение
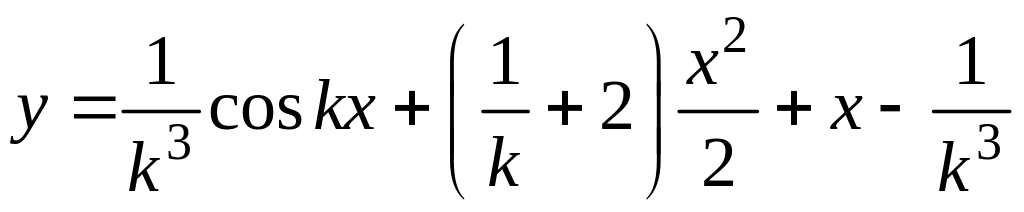 .
Как и в общем случае, получилось, что
.
Как и в общем случае, получилось, что
![]() ,
,
![]() ,
,
![]() .
.
Замечание. Можно было брать неопределенные интегралы, но тогда для определения произвольных постоянных С1, С2 и С3 пришлось бы решать систему трех алгебраических уравнений с тремя неизвестными.
Дифференциальное уравнение, не содержащее явно искомую функцию у.
Предположим, что уравнение не содержит явно неизвестную функцию у и ее производные до порядка (k 1) включительно.
![]() .
.
Введем новую
неизвестную функцию
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
…,
,
…,
![]() и уравнение сводится к уравнению
и уравнение сводится к уравнению
![]() ,
порядок которого
,
порядок которого
![]() .
Решив его, найдем функцию
,
т.е. получим уравнение вида .
.
Решив его, найдем функцию
,
т.е. получим уравнение вида .
Пример
9.12.2. Решить
уравнение
![]() .
.
Решение. В
уравнении нет неизвестной функции у.
Введем замену
![]() ,
тогда
,
тогда
![]() и уравнение принимает вид
и уравнение принимает вид
![]() ,
или
,
или
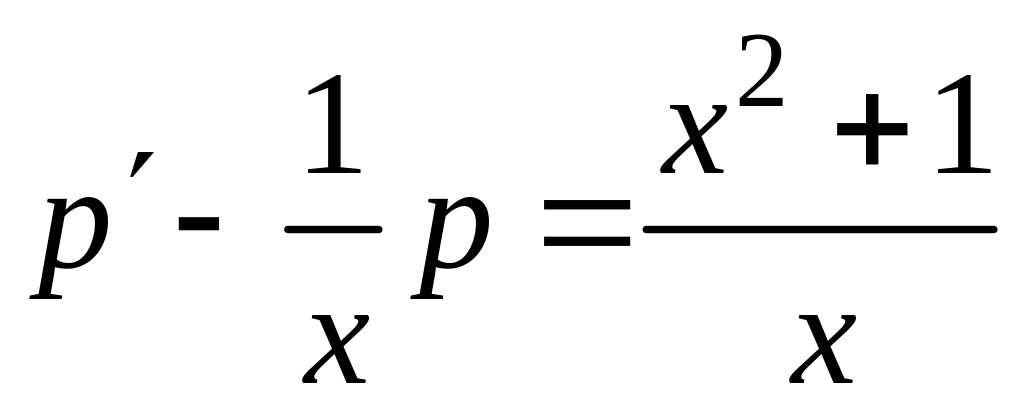 .
Таким образом, получено линейное
неоднородное дифференциальное уравнение
первого порядка. Решим его методом
Бернулли.
.
Таким образом, получено линейное
неоднородное дифференциальное уравнение
первого порядка. Решим его методом
Бернулли.
![]() ,
,
![]()
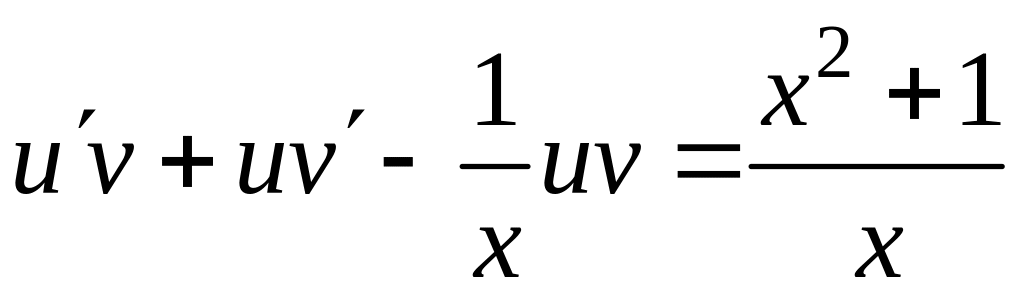 .
.
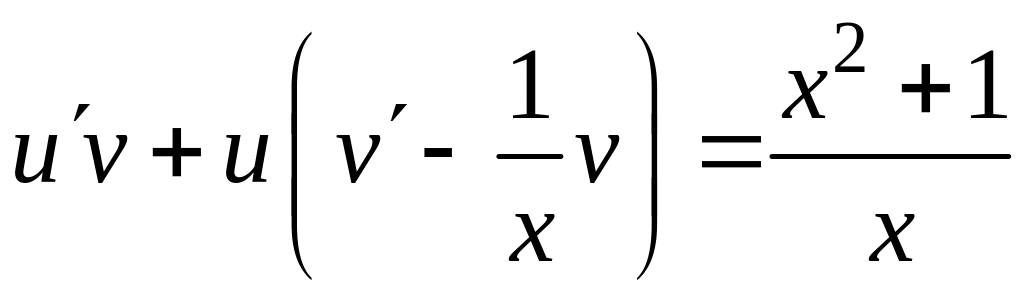

Решаем первое
уравнение системы
![]()
![]()
![]() (С=0)
v
= x.
Подставляя v
= x
во второе
уравнение системы, получим:
(С=0)
v
= x.
Подставляя v
= x
во второе
уравнение системы, получим:
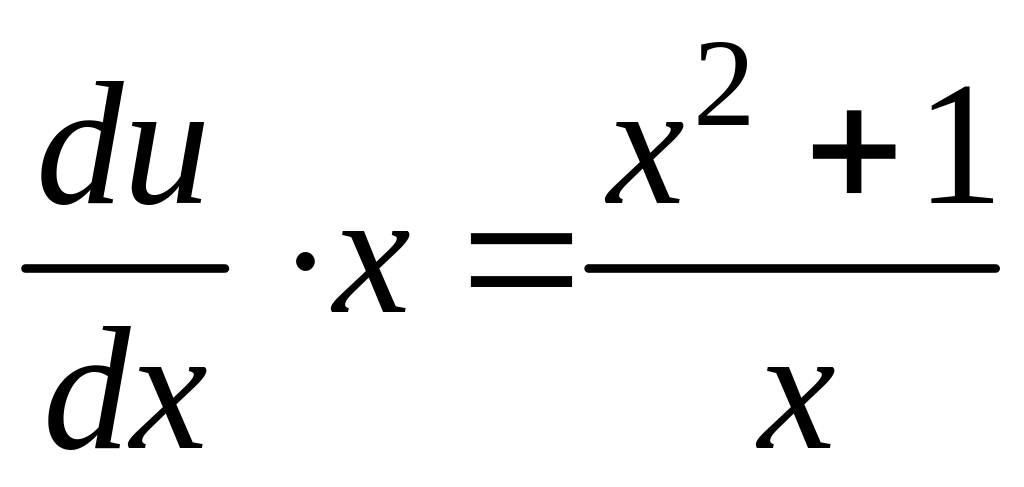
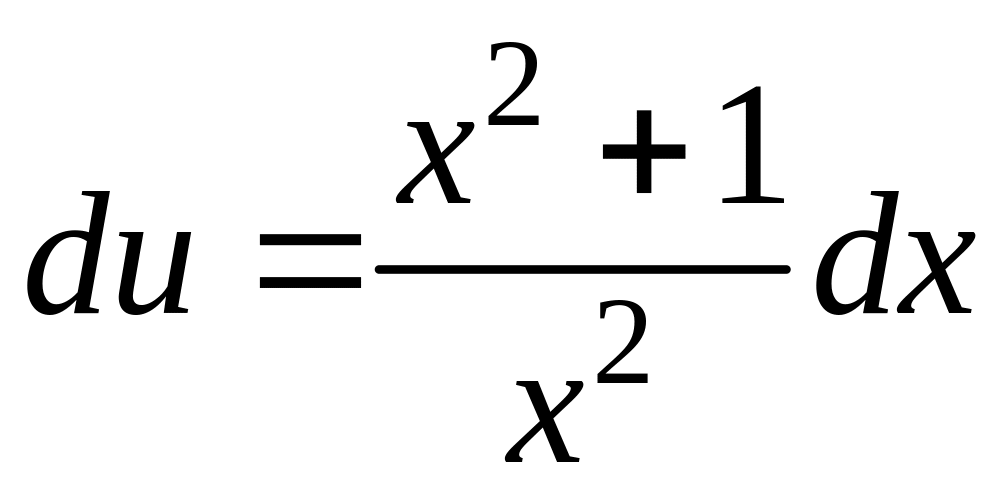
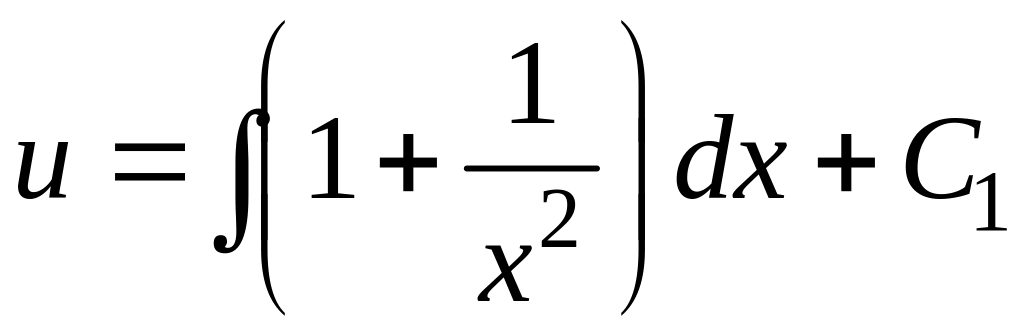 ,
т.е.
,
т.е.
![]() .
Тогда p=uv,
.
Тогда p=uv,
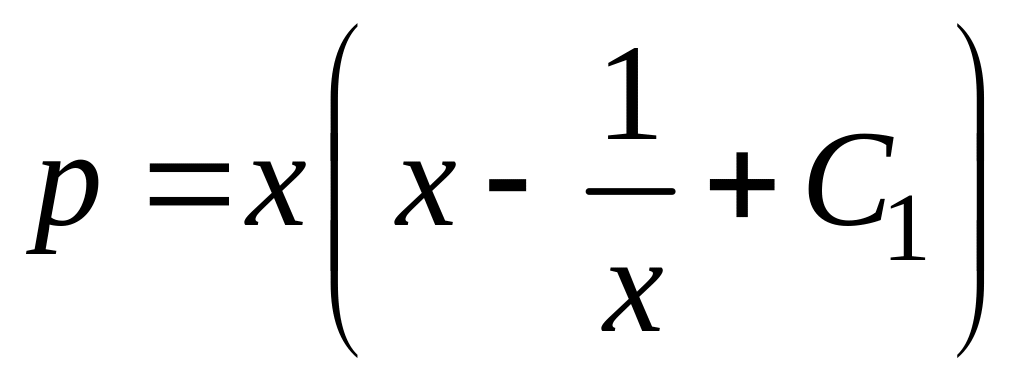 .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
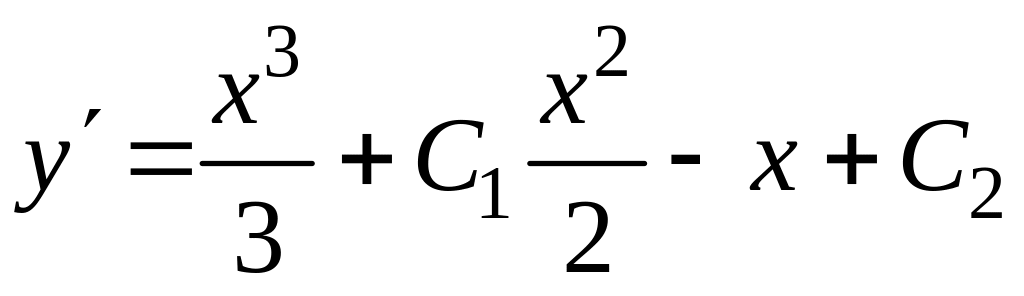
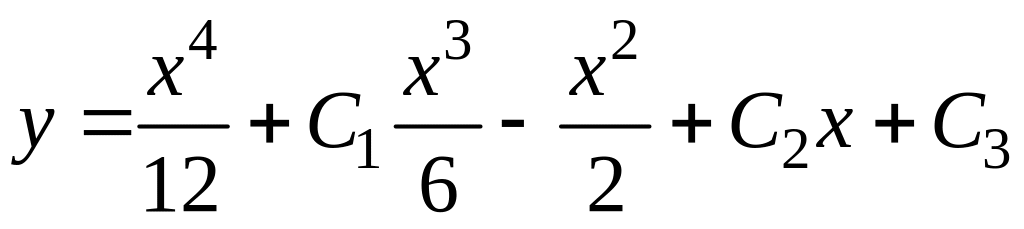 – искомое общее решение.
– искомое общее решение.
В случае дифференциального уравнения второго порядка
![]()
замена
![]() ,
,
![]() приводит к дифференциальному уравнению
первого порядка
приводит к дифференциальному уравнению
первого порядка
![]() .
.
Дифференциальные уравнения, не содержащие явно независимую переменную х.
Рассмотрим дифференциальное уравнение второго порядка
![]() ,
,
не содержащее в
явном виде х
(х,
вообще говоря, присутствует в уравнении,
так как у,
,
![]() являются функциями от х).
являются функциями от х).
Для решения этого уравнения снова положим
![]() ,
,
но теперь мы будем считать p = p(y) – функцией от у (а не от х, как в предыдущем случае). Тогда по правилу дифференцирования сложной функции
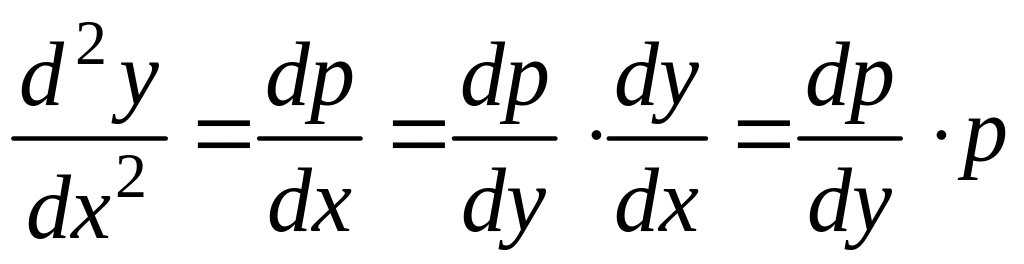 .
.
Подставляя в уравнение выражения и , получим дифференциальное уравнение первого порядка относительно вспомогательной функции р
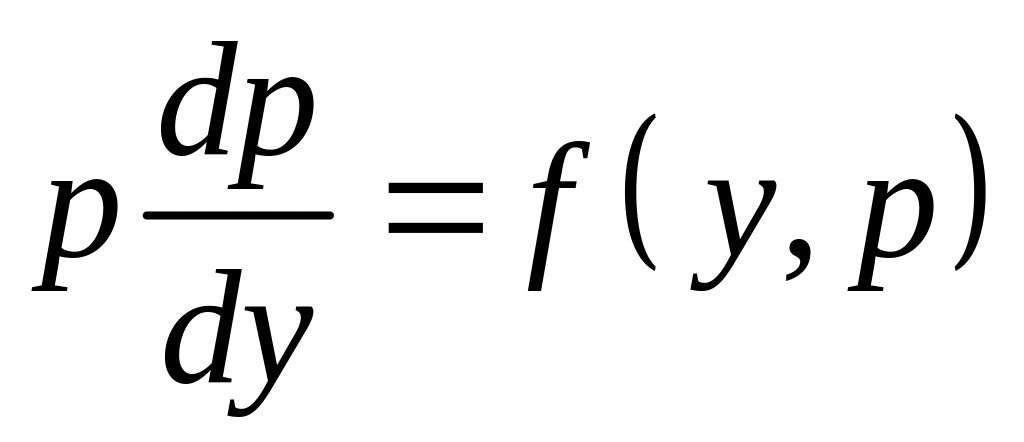 .
.
Интегрируя его, найдем р как функцию от у и произвольной постоянной С1:
![]() .
.
Но
![]() ,
поэтому
,
поэтому
![]()
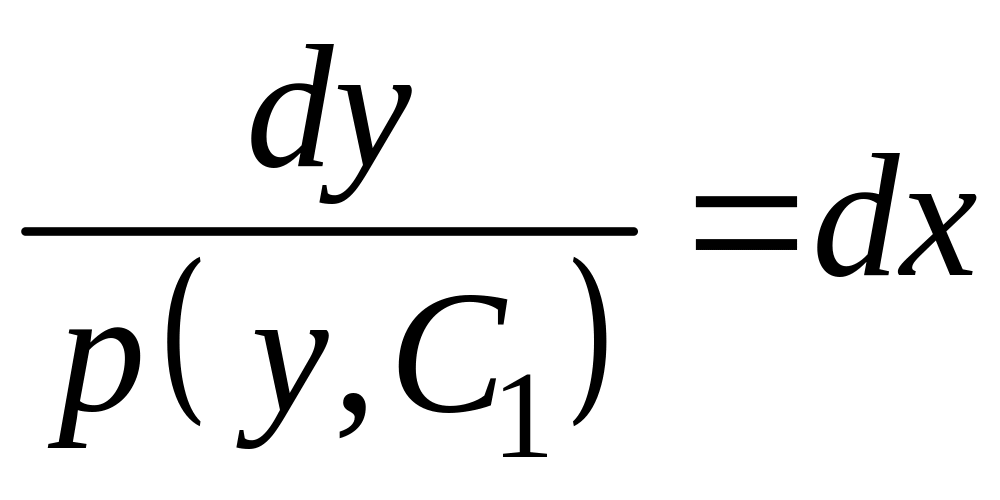
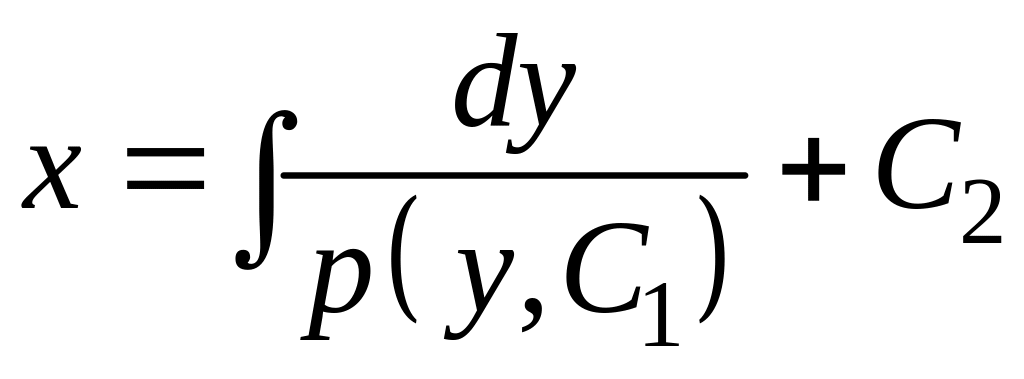 .
.
Пример
9.12.3. Решить
задачу Коши:
![]() ,
,
![]() .
.
Решение. В
уравнении нет х.
Введем замену
![]() ,
тогда
,
тогда
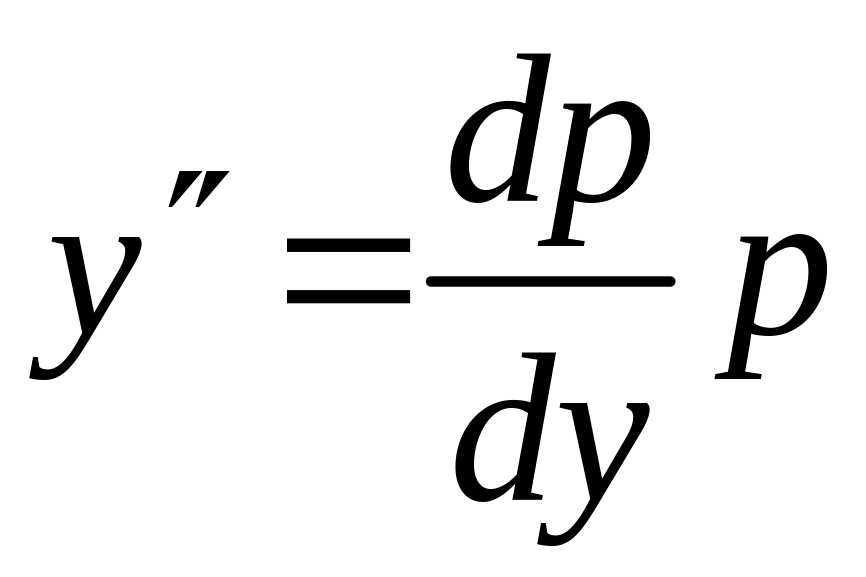 и уравнение принимает вид
и уравнение принимает вид
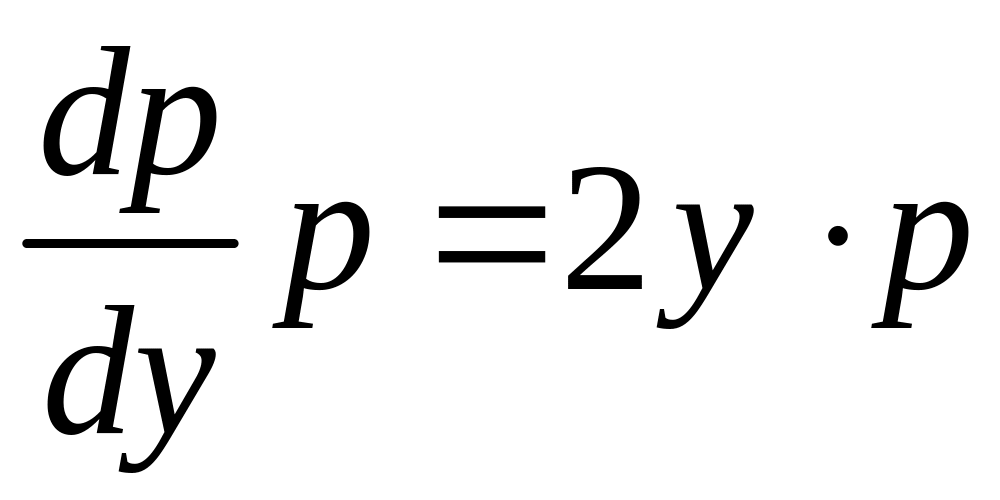
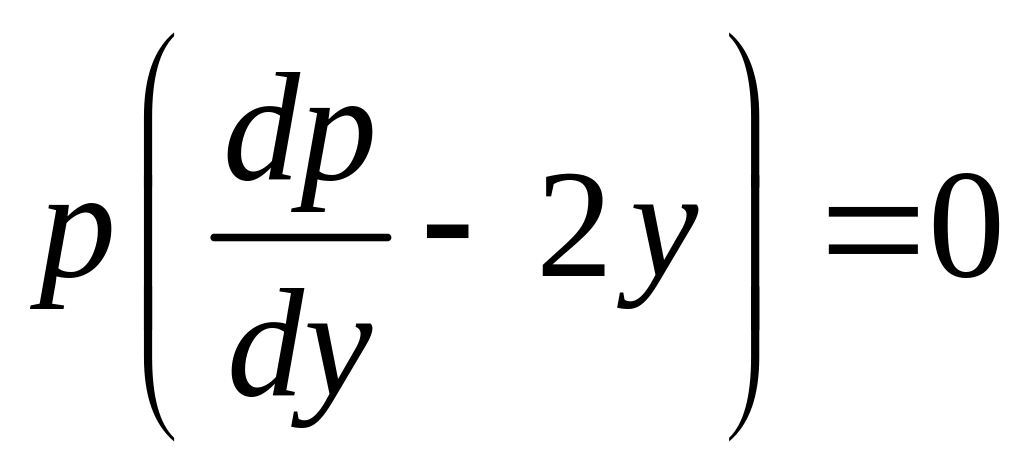 .
.
Отсюда, или р
= 0, или
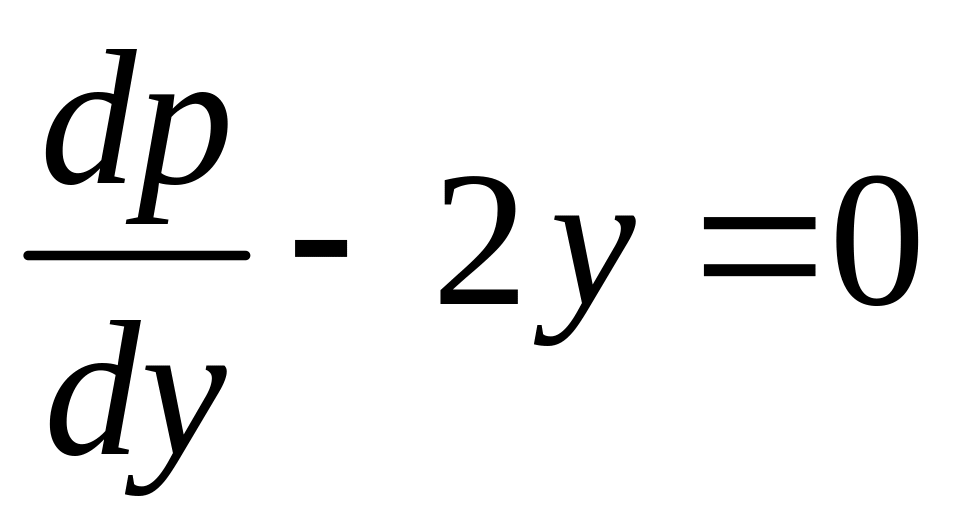 .
В первом случае р
= 0
.
В первом случае р
= 0
![]()
у = С.
Но это решение не удовлетворяет начальным
условиям (если у
= С,
,
т.е.
![]() ).
Во втором случае
).
Во втором случае
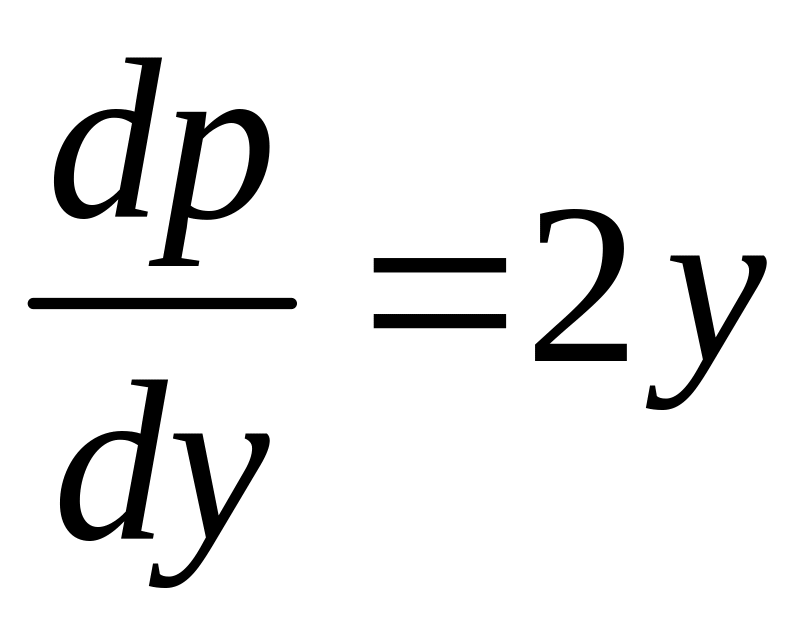
![]()
![]() ,
т.е.
,
т.е.
![]() .
.
Подставляя начальные условия , получаем 1 = 1+С1, т.е.
С1
= 0, так что
![]()
![]()
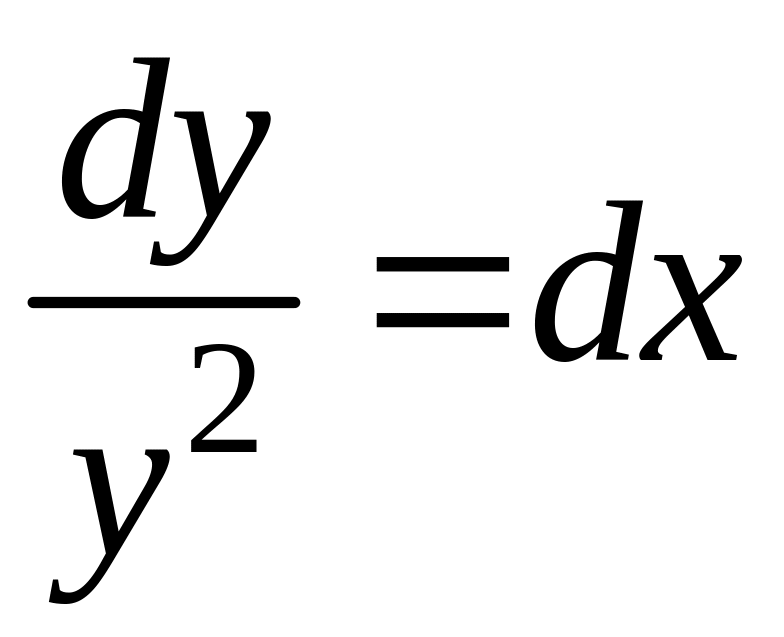
![]()
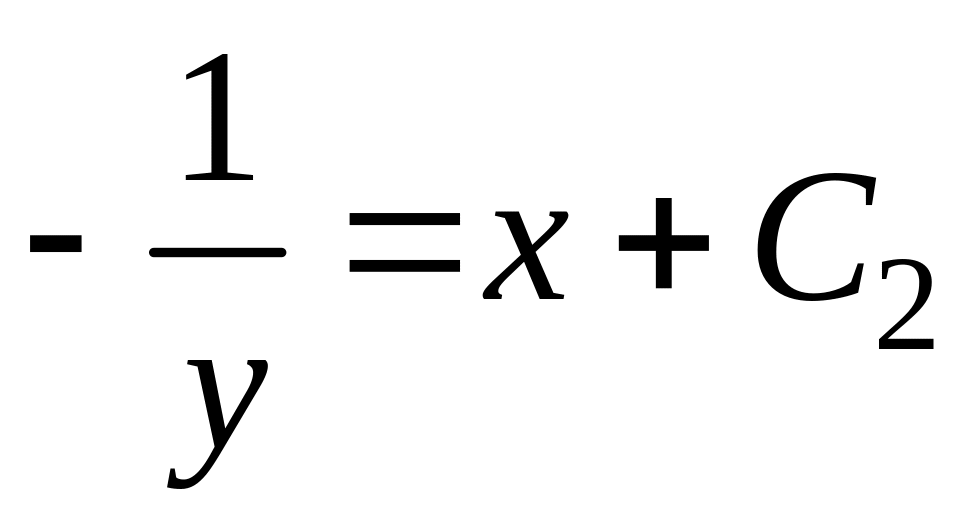
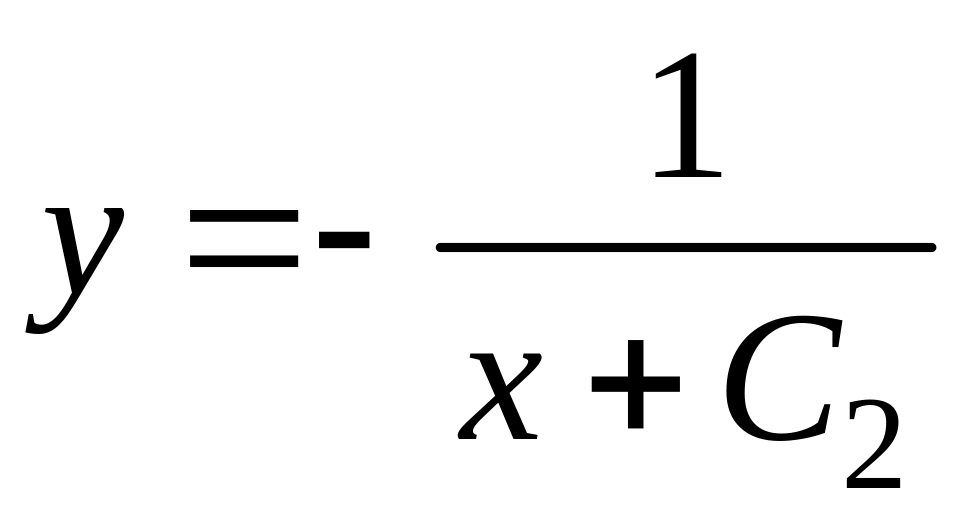 .
Из начального условия
.
Из начального условия
![]() находим С2:
находим С2:
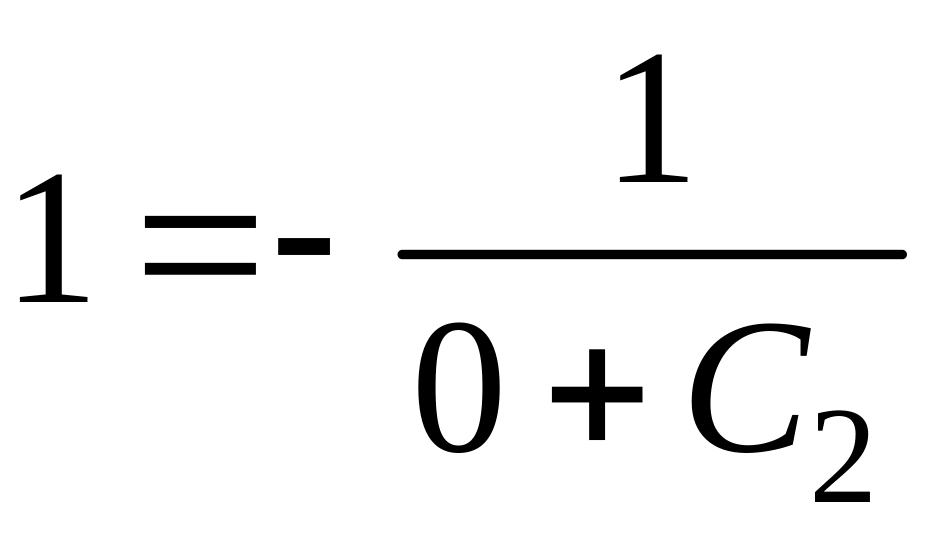
С2=-1.
таким образом,
С2=-1.
таким образом,
![]() – искомое частное решение.
– искомое частное решение.
В уравнении общего
вида
![]() замена
замена
![]() понижает его порядок на единицу.
понижает его порядок на единицу.
