
- •9.16. Линейные однородные дифференциальные уравнения
- •I. Основные понятия теории дифференциальных уравнений.
- •III. Линейные дифференциальные уравнения первого порядка
- •Учебный модуль №9 «Дифференциальные уравнения» Введение
- •Дидактические цели обучения
- •Учебно-методическая карта модуля
- •Графическая схема модуля
- •Информационная таблица «Дифференциальные уравнения»
- •9.1. Физические задачи, приводящие к дифференциальным уравнениям
- •9.2. Основные понятия теории дифференциальных уравнений
- •9.3. Дифференциальные уравнения первого порядка. Задача Коши
- •9.4. Дифференциальные уравнения с разделенными и разделяющимися переменными
- •9.5. Однородные дифференциальные уравнения и приводящиеся к ним
- •9.6. Линейные дифференциальные уравнения первого порядка
- •9.7. Уравнение Бернулли
- •9.8. Дифференциальные уравнения в полных дифференциалах
- •9.9. Особые решения дифференциальных уравнений первого порядка
- •9.10. Модели прикладных задач с применением дифференциальных уравнений
- •9.11. Дифференциальные уравнения высших порядков. Задача Коши. Понятие общего и частного решений
- •9.12. Дифференциальные уравнения, допускающие понижение порядка
- •9.13. Понятие о краевых задачах для обыкновенных дифференциальных уравнений
- •9.14. Линейные дифференциальные уравнения высших порядков
- •9.15. Линейные однородные дифференциальные уравнения, свойства их решений. Определитель Вронского. Условия линейной зависимости и независимости решений
- •9.16. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
- •9.17. Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных
- •9.18. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •9.19. Системы дифференциальных уравнений. Решение систем дифференциальных уравнений с постоянными коэффициентами
- •Вопросы к экзамену по модулю №9
- •Дифференциальные уравнения в полных дифференциалах.
9.9. Особые решения дифференциальных уравнений первого порядка
Из геометрического смысла дифференциального уравнения следует, что его интегральная кривая в каждой своей точке имеет касательную, совпадающую с направлением поля, порожденного этим уравнением. Отсюда вытекает, что все интегральные кривые дифференциального уравнения (если они существуют), проходящие через точку, должны касаться друг друга.
Теперь можно определить особое решение дифференциального уравнения с геометрической точки зрения. Решение дифференциального уравнения называется особым, если через любую точку соответствующей ему интегральной кривой проходит, кроме нее, еще и другая, касающаяся ее, интегральная кривая данного уравнения.
Кривая, через каждую точку которой проходит хотя бы еще одна кривая некоторого семейства, имеющая ту же касательную в данной точке, что и кривая семейства, называется огибающей данного семейства.
Из сказанного следует, что особое решение дифференциального уравнения является огибающей семейства интегральных кривых (общего интеграла) этого уравнения.
Пример
9.9.1. Найти
особое решение уравнения
![]() .
.
Решение. Разрешим уравнение относительно .
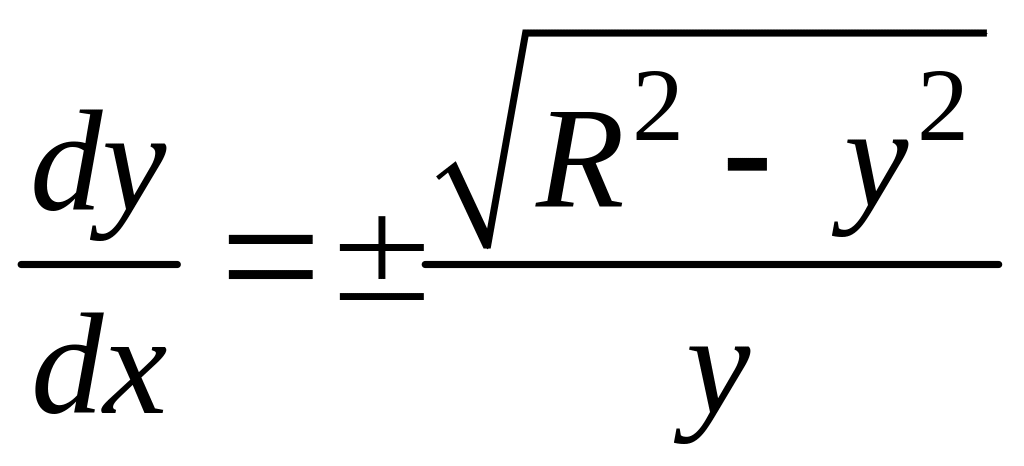
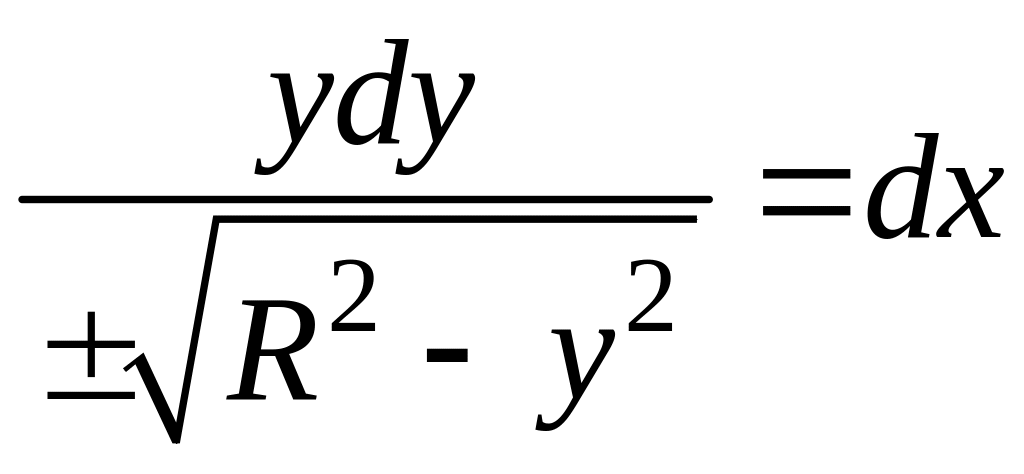
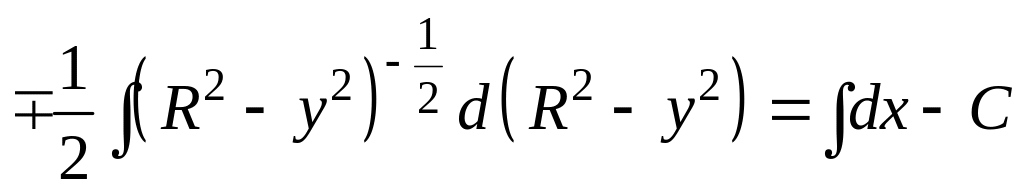
![]()
![]()
![]() – общий интеграл
данного уравнения.
– общий интеграл
данного уравнения.
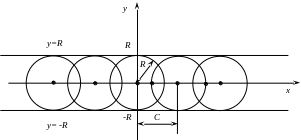
Легко видеть, что
семейство интегральных линий представляет
собой семейство окружностей радиуса
R
с центром на оси абсцисс. Огибающей
семейства кривых будет пара прямых
![]() .
.
Функции
удовлетворяют исходному дифференциальному
уравнению
![]() .
Следовательно,
– особые решения данного уравнения.
.
Следовательно,
– особые решения данного уравнения.
9.10. Модели прикладных задач с применением дифференциальных уравнений
Составление дифференциальных уравнений является важным и вместе с тем трудным вопросом. Универсального метода, пригодного во всех случаях, указать нельзя. Необходимо приобретение опыта и определенных навыков в решении различных задач, что достигается разбором большого количества задач и самостоятельным решением аналогичных примеров. Необходимо также знание данной прикладной дисциплины.
Составление дифференциального уравнения по условию задачи (механической, физической, химической, технической или любой другой) состоит в определении математической зависимости между переменными величинами и их приращениями, которые сразу же заменяются соответствующими дифференциалами.
В большинстве случаев модель прикладных задач с применением обыкновенных дифференциальных уравнений сводится к следующему:
подробный разбор условий задачи и составление чертежа, поясняющего его суть;
составление дифференциального уравнения рассматриваемого процесса;
интегрирование этого уравнения и определение его общего решения;
определение частного решения задачи на основании данных начальных условий;
определение по мере необходимости вспомогательных параметров (например, коэффициента пропорциональности и т.д.) с использованием для этой цели дополнительных условий задачи;
вывод общего закона рассматриваемого процесса и числовое определение искомых величин;
анализ ответа и проверка исходного положения задачи.
В качестве примера рассмотрим задачу о радиоактивном распаде.
Задача 9.10.1. Скорость распада радия прямо пропорциональна наличной его массе. Определить, какой процент массы m0 радия распадется через 200 лет, если известно, что период полураспада радия (период времени, по истечении которого распадается половина наличной массы радия) равен 1590 лет.
Решение. Скорость
распада радия измеряется его количеством,
распавшимся в единицу времени. За малый
промежуток времени
![]() ,
истекший с некоторого момента времени
t,
количество распавшегося радия равно
,
истекший с некоторого момента времени
t,
количество распавшегося радия равно
![]() ,
где m
– количество радия в данный момент
времени, k
– коэффициент пропорциональности. Это
же количество, взятое с отрицательным
знаком (масса убывает), равно приращению
массы за время
:
,
где m
– количество радия в данный момент
времени, k
– коэффициент пропорциональности. Это
же количество, взятое с отрицательным
знаком (масса убывает), равно приращению
массы за время
:
![]() .
.
Обе части равенства
делим на
и переходим к пределу при
![]() .
Тогда
.
Тогда ![]() .
.
Разделяем переменные:
![]() .
.
Интегрируя уравнение
, находим ![]() или после потенцирования
или после потенцирования
![]() .
.
Начальное условие: ![]() при t
= 0.
при t
= 0.
![]() .
.
Таким образом:
![]() .
.
Коэффициент k определяем из дополнительного условия:
при t
= 1590 ![]() .
.
![]() ,
,
![]() .
.
Искомая функция
![]() .
.
Количество радия,
не распавшегося через 200 лет,
![]() (что составляет 91,5%).
(что составляет 91,5%).
Следовательно, через 200 лет распадется лишь 8,5% радия.
Интересующихся моделями прикладных задач с помощью дифференциальных уравнений отправляем к учебному пособию [14].
