9.6. Линейные дифференциальные уравнения первого порядка
Уравнение
,
линейное относительно
неизвестной функции и ее производной
(т.е. содержащее у
и
в первой степени), называется линейным
дифференциальным уравнением первого
порядка. Здесь p(x)
и f(x)
– непрерывные на
функции, либо постоянные числа.
Если
,
то уравнение
называется линейным
однородным
дифференциальным уравнением (левая
часть этого уравнения является однородной
функцией относительно у
и
,
так как
).
Если
,
то уравнение называется неоднородным.
Существует несколько методов интегрирования линейных дифференциальных уравнений первого порядка. Рассмотрим некоторые из них.
Метод подстановки (Бернулли)
По этому методу искомое решение уравнения будем искать в виде
,
где
и
- некоторые непрерывно дифференцируемые
функции. Подставляя y
= uv
и
в , получаем
или
.
Выберем функцию таким образом, чтобы
,
после чего от уравнения остается
.
В результате получили систему двух уравнений
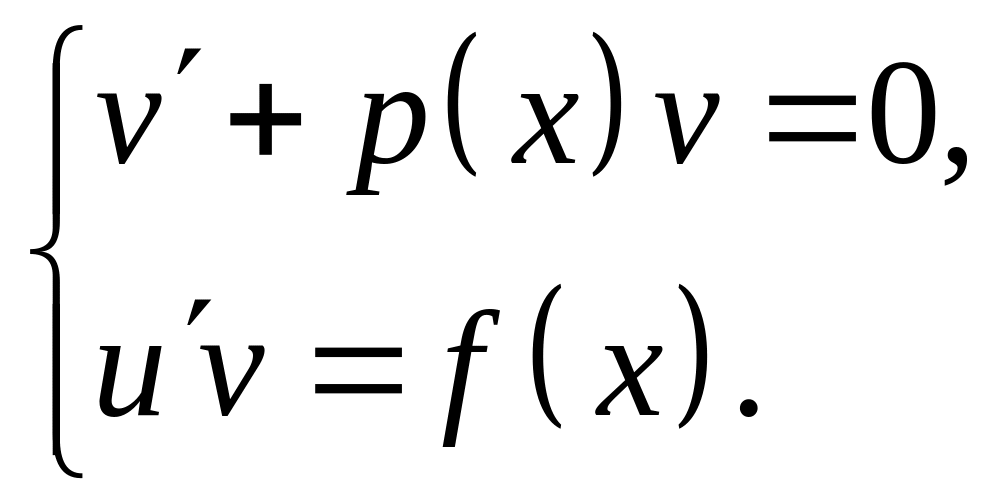
Сначала решаем
первое уравнение системы, которое
является линейным однородным
дифференциальным уравнением относительно
v
и
.
Покажем, что оно, в то же время, и уравнение
с разделяющимися переменными.
.
Подставляя функцию v во второе уравнение системы , получаем еще одно уравнение с разделяющимися переменными
,
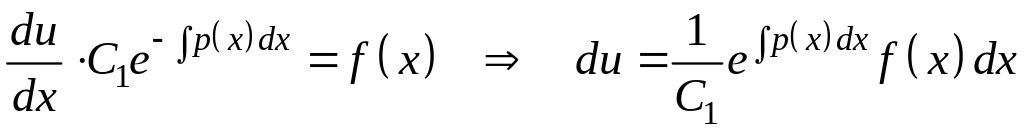откуда
.
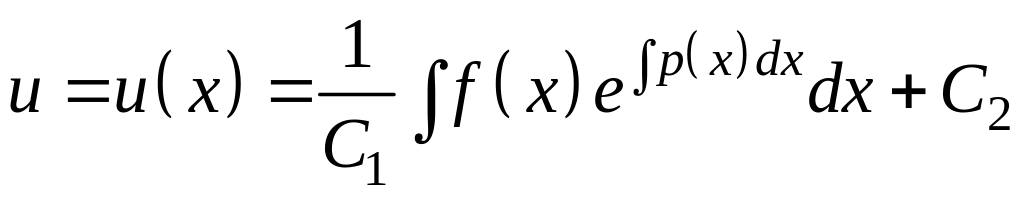Таким образом, , т.е.
.
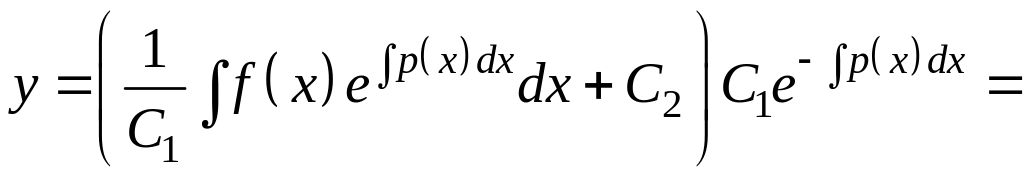
Так как С1 и С2 – произвольные постоянные, то С1С2 тоже произвольная постоянная, которую можно обозначить через С. В итоге получаем, что общим решением неоднородного дифференциального уравнения будет
.
Поскольку при
перемножении функций
и
постоянная С1
во втором слагаемом сократилась, то в
качестве функции
можно было взять
.
Пример
9.6.1. Решить
уравнение
.
Решение. Пусть y = uv, . Тогда
.
Составим систему
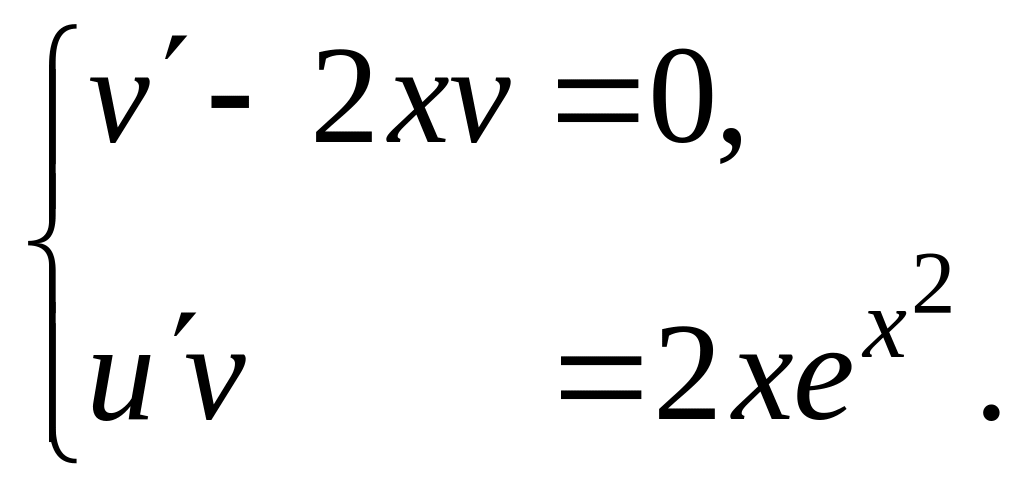
Решаем первое
уравнение
(постоянную здесь не берем).
Подставляем
во второе уравнение системы
.
В итоге находим, что общее решение данного уравнения
, 
.
Метод вариации произвольного постоянного (метод Лагранжа)
Найдем общее решение однородного дифференциального уравнения . Разделив в нем переменные, получим
,
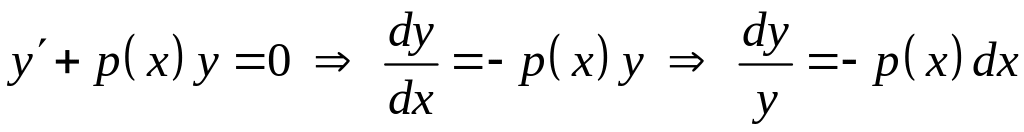
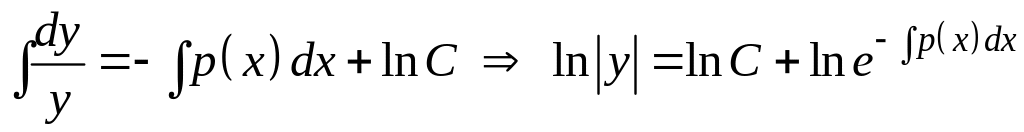
где С – произвольная постоянная.
По методу вариации (в переводе на русский язык, изменения) произвольной постоянной общее решение неоднородного уравнения ищется в виде
,
в котором
– неизвестная дифференцируемая функция.
Найдем
.
Подставляя y
и
в , получаем
,
откуда
.
Итак, функция
найдена. Подставляя ее в , находим общее
решение уравнения
,
совпадающее с решением .
Пример
9.6.2. Найти
частное решение дифференциального
уравнения
,
удовлетворяющее начальному условию
.
Решение. В
начале решаем соответствующее однородное
уравнение
.
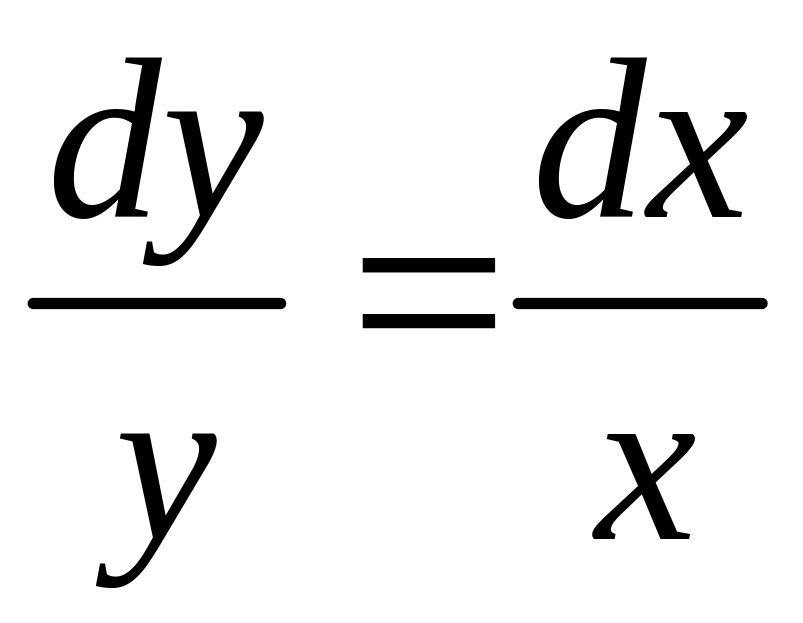
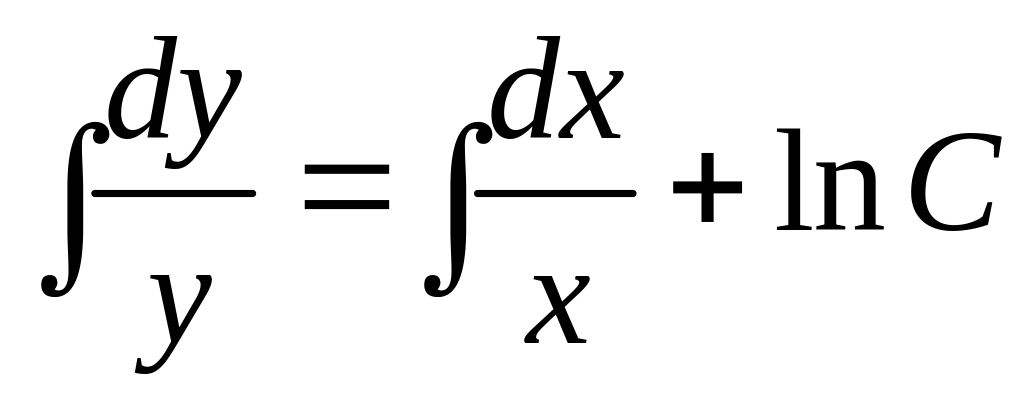
В соответствии с
методом Лагранжа общее решение ищем в
виде
.
Находим
.
Тогда
и
,
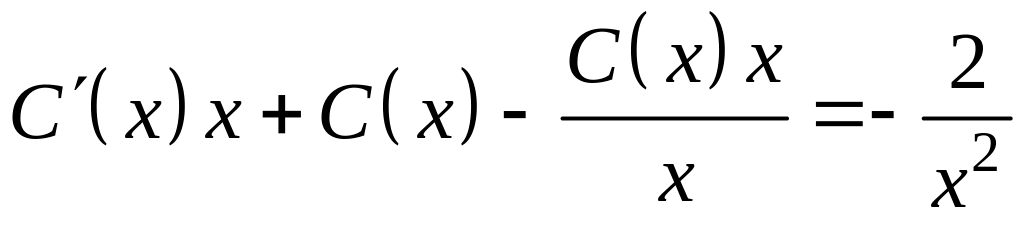
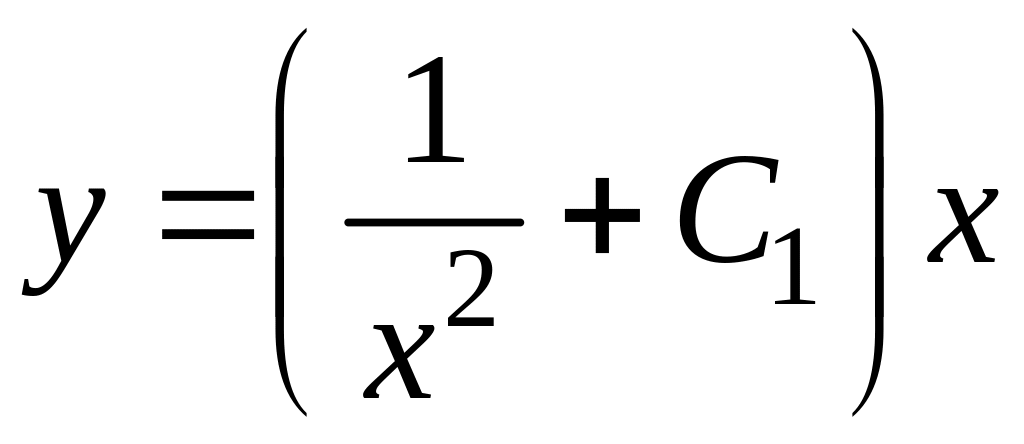или
будет общим решением данного уравнения.
Из условия
имеем
.
Итак, искомым
частным решением данного уравнения,
удовлетворяющим начальному условию
,
является функция
.
Общее решение
уравнения можно сразу найти по формуле
, подставив туда
и
и взяв три интеграла.
Замечание. В приложениях часто встречаются линейные уравнения с постоянными коэффициентами
,
где a и b – постоянные. Его можно решить путем разделения переменных:
.
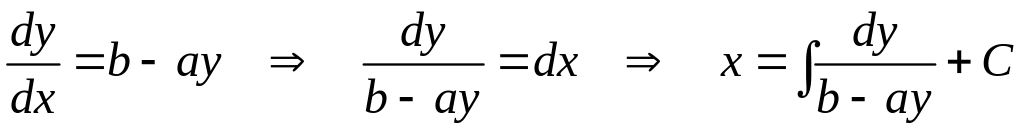