9.19. Системы дифференциальных уравнений. Решение систем дифференциальных уравнений с постоянными коэффициентами
При решении многих
задач требуется найти функции
,
,
…,
,
которые удовлетворяют системе
дифференциальных уравнений, содержащих
аргумент х,
искомые функции у1,
у2,
…, yn
и их производные.
Рассмотрим систему дифференциальных уравнений первого порядка.
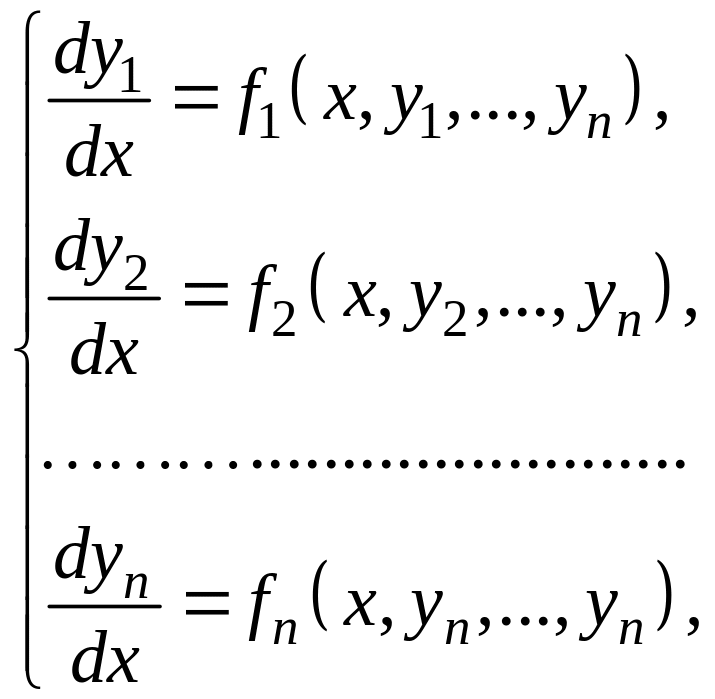
где у1, у2, …, yn – искомые функции, х – аргумент.
Такая система, когда в левой части уравнений стоят производные первого порядка, а правые части не содержат производных, называется нормальной.
Проинтегрировать систему – значит определить функции у1, у2, …, yn, удовлетворяющие системе уравнений и данным начальным условиям
,
,
…,
.
В дифференциальные уравнения системы могут входить производные высших порядков. В этом случае получается система дифференциальных уравнений высших порядков.
Рассмотрим систему линейных однородных дифференциальных уравнений с постоянными коэффициентами.
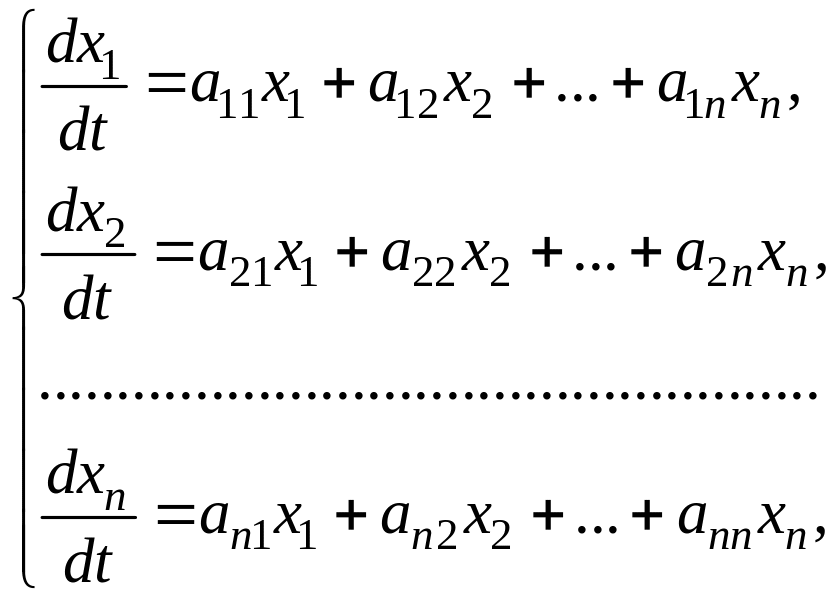
где коэффициенты
– постоянные числа.
Будем искать частные решения системы в следующем виде:
,
,
…,
.
Требуется определить
постоянные 1,
2,
…, n
и k
так, чтобы функции
,
,…,
удовлетворяли системе . Подставляя их
в систему, получим,
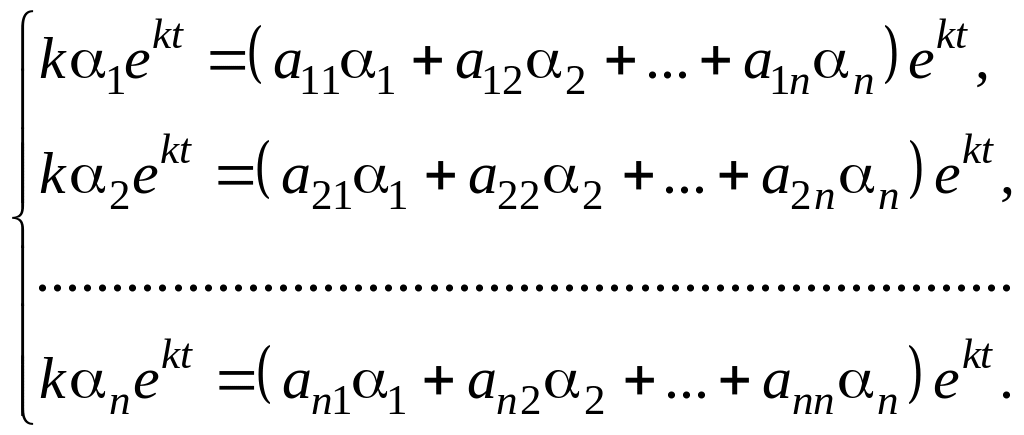
Сократим на
обе части уравнений. Перенося все члены
в одну сторону и собирая коэффициенты
при 1,
2,
…, n,
получим систему:
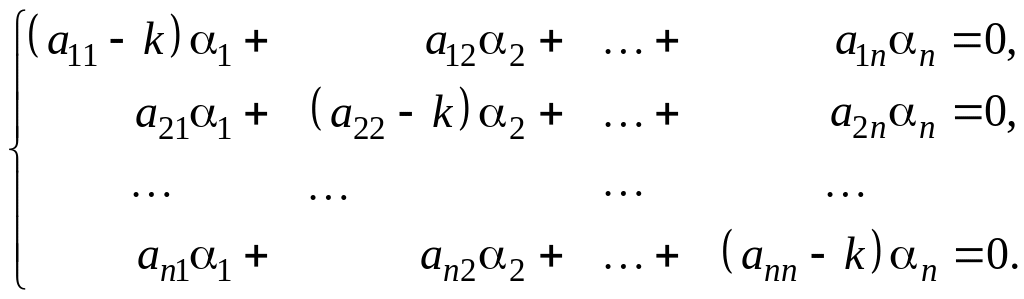
Система это система линейных однородных алгебраических уравнений относительно 1, 2, …, n. Выпишем определитель этой системы
.
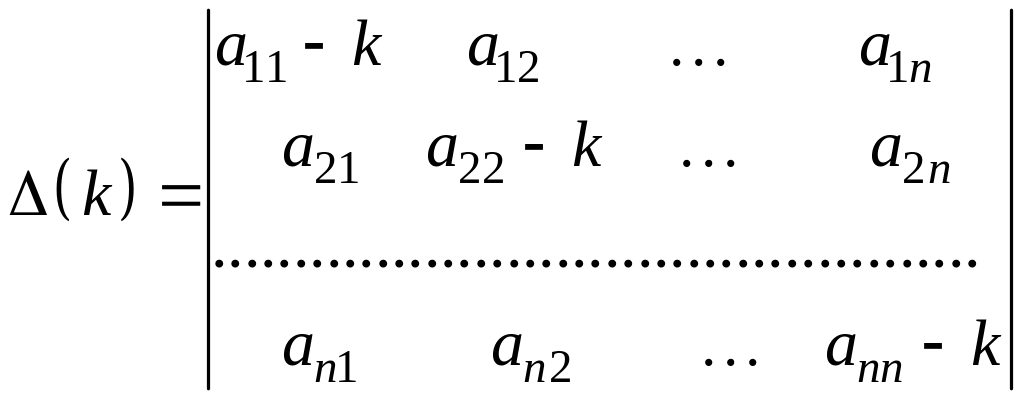Если k
таково, что
,
то система имеет только нулевые решения
1
= 0, 2
= 0, …, n
= 0, а формулы дают только тривиальные
решения
.
Таким образом,
нетривиальные решения мы получим только
при таких k,
при которых определитель
,
т.е.
.
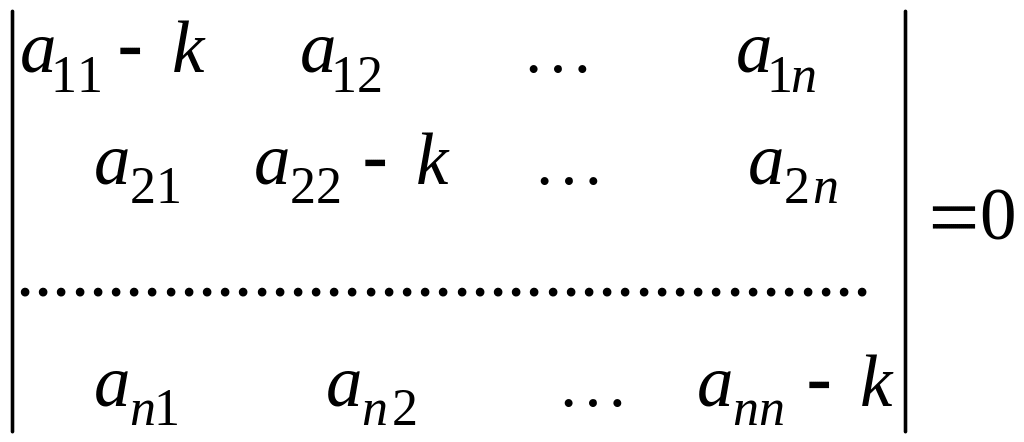Это уравнение называется характеристическим уравнением системы , оно является алгебраическим уравнением n-го порядка для определения k.
Рассмотрим только
случай, когда корни характеристического
уравнения действительные и различные
: k1
k2
…
kn.
Для каждого корня
напишем систему и определим числа
,
,
…,
.
Таким образом, получаем:
для корня k1: 
,
,
…,
;
для корня k2: 
,
,
…,
;
………………………………………………………………………………….
для корня kn: 
,
,
…,
.
Путем непосредственной подстановки в уравнения системы можно убедиться, что система функций
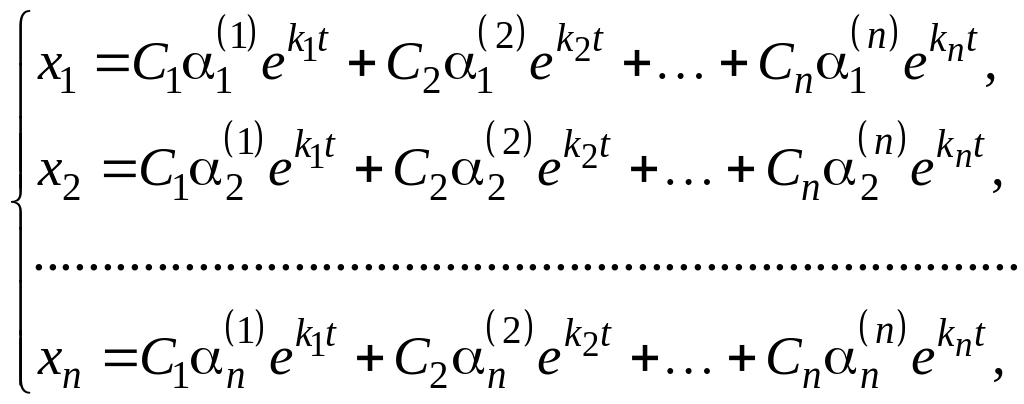
где С1, С2, …, Сn – произвольные постоянные, тоже является решением этой системы.
В случае комплексных
корней
применяются формулы Эйлера
,
тогда частными решениями будут
и
.
Соответствующий пример рассматривается
в практической части модуля.
Пример
9.19.1. Решить
систему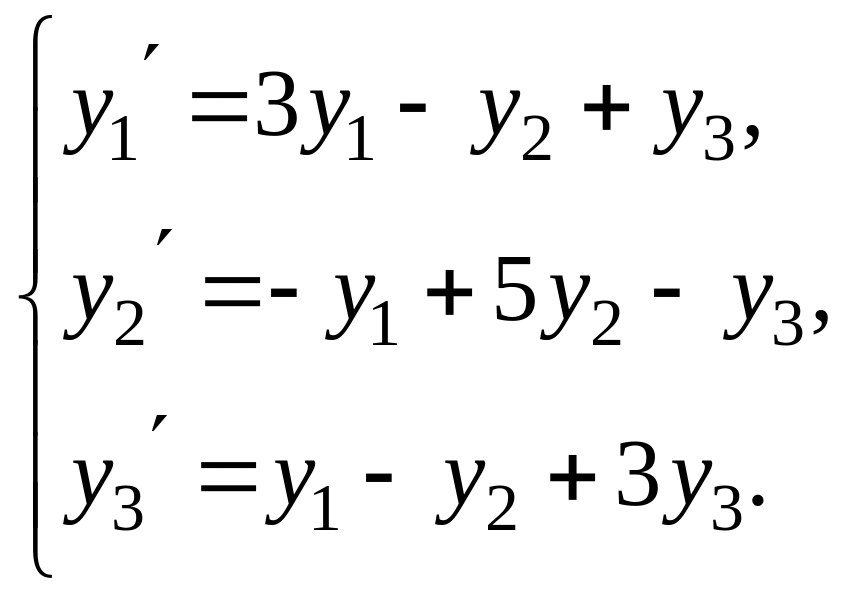 
Решение. Характеристическое
уравнение
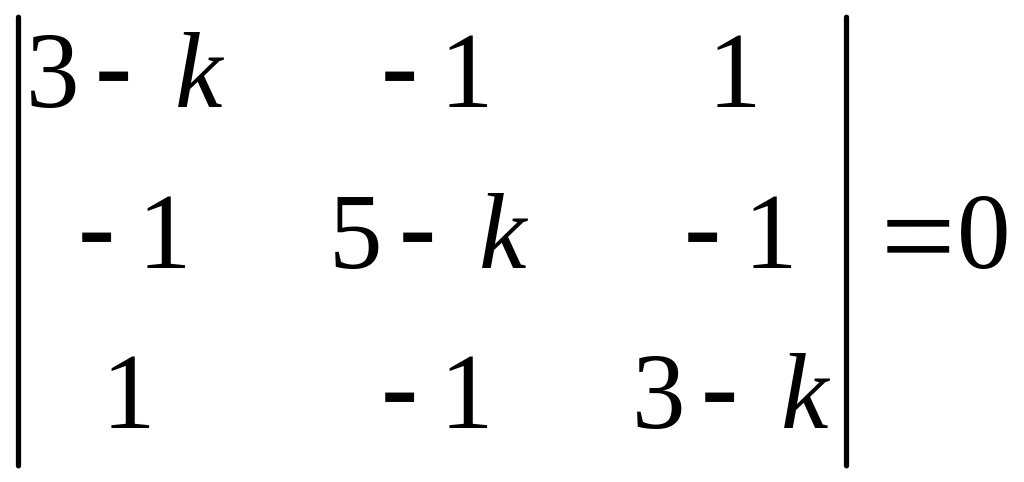
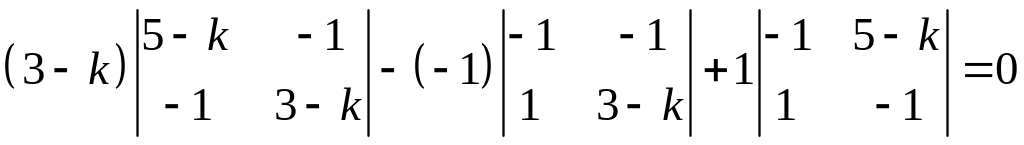
. Легко
угадать один корень
.
Разделив по правилу деления многочленов
на
,
получим
,
.
Для система имеет вид
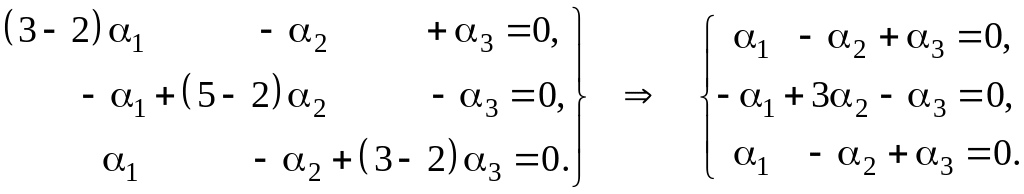
Решим эту систему
методом Гаусса. Имеем (третье уравнение
совпадает с первым и мы его отбрасываем):
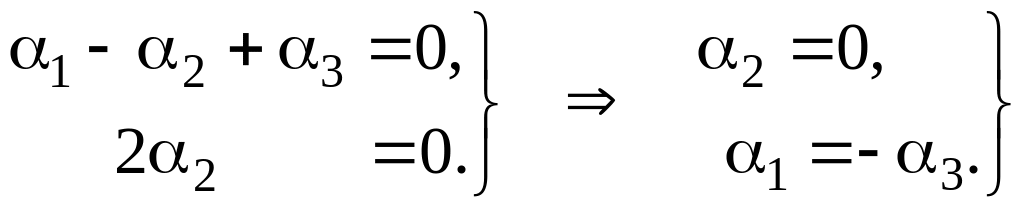Положим
,
тогда
,
т.е.
,
,
.
Точно так же для
получим
,
,
,
а для
:
,
,
.
Таким образом,
для
: 
,
,
;
для
: 
, 
, 
;
для
: 
; 
; 
.
Тогда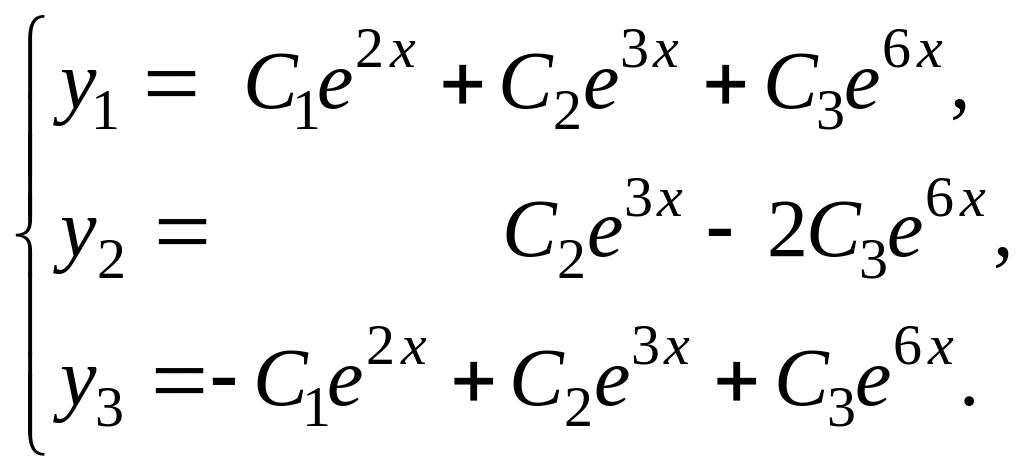 
– общее решение исходной системы.
Системы дифференциальных уравнений можно решать сведением к одному дифференциальному уравнению высшего порядка. Покажем, как это делается на примере.
Пример 9.19.2. Решить задачу Коши для системы
.
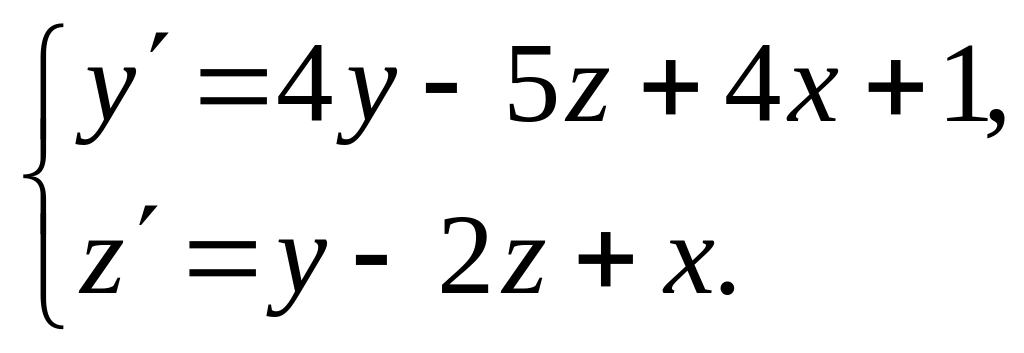
Решение. Из
второго уравнения
.
у
и
подставляем в первое уравнение, тогда
,
т.е. получили линейное неоднородное
дифференциальное уравнение с постоянными
коэффициентами. Его общее решение
.
Составляем и решаем
характеристическое уравнение
,
.
,
т.е.
,
где
= 0 не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде
,
т.е.
и
,
а
.
и
Таким
образом,
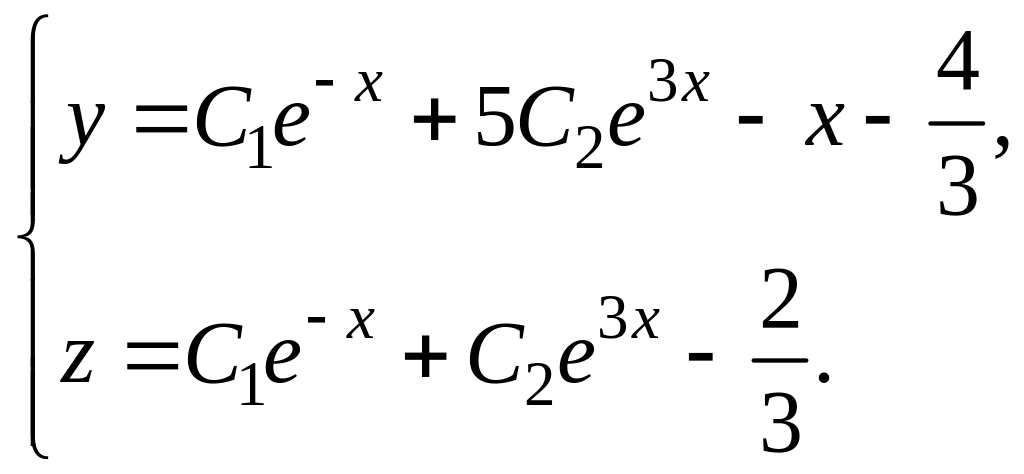– общее решение
данной системы.
Используя начальные условия , получаем
,
.
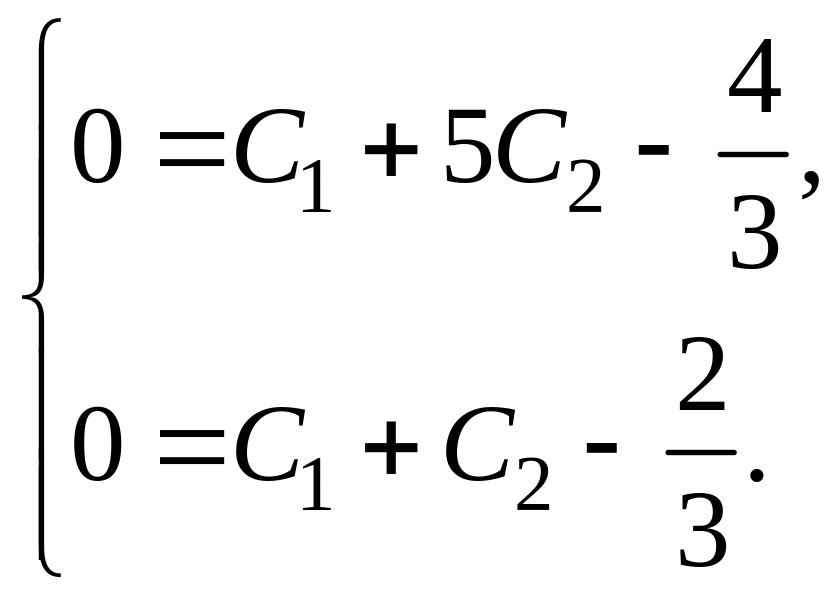
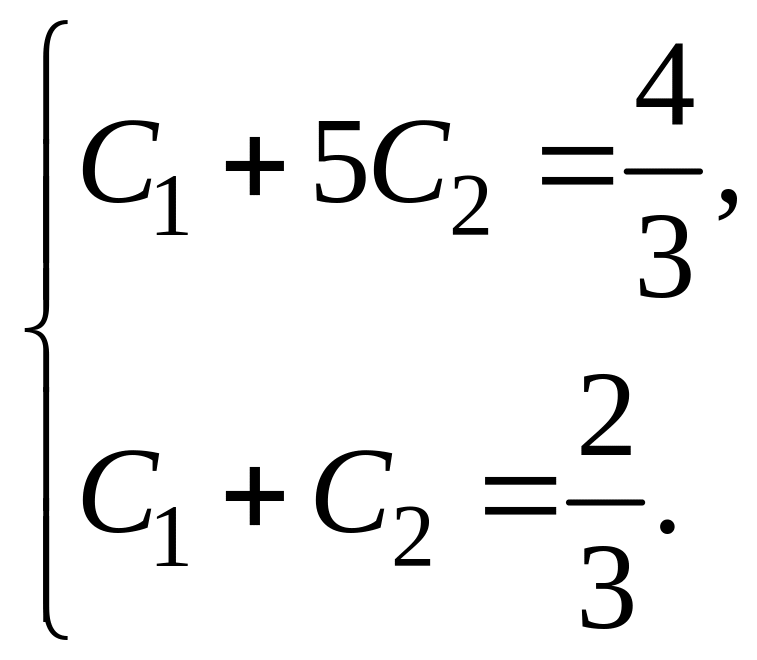
Искомое решение задачи Коши имеет вид:
