9.17. Линейные неоднородные дифференциальные уравнения. Метод вариации произвольных постоянных
Рассмотрим сначала линейное неоднородное уравнение второго порядка
,
где а1, а2, f(x) – либо непрерывные функции, либо постоянные числа. Структура общего решения такого уравнения определяется следующей теоремой.
Теорема 9.17.1. Общее решение неоднородного уравнения представляет собой сумму какого-нибудь частного решения этого уравнения уч и общего решения уодн соответствующего однородного уравнения
.
Из теоремы следует, что у=уодн + уч.
Таким образом, если известно общее решение соответствующего однородного уравнения, то основная задача решения неоднородного уравнения состоит в нахождении какого-либо его частного решения.
Укажем общий метод нахождения частного решения неоднородного уравнения.
Метод вариации произвольных постоянных (Лагранжа)
Предположим известно общее решение однородного уравнения
,
где у1 и у2 – линейно независимые частные решения однородного уравнения.
Будем искать частное решение неоднородного уравнения в виде
,
рассматривая С1 и С2 как некоторые пока неизвестные функции.
Продифференцируем равенство :
.
Подберем искомые
функции
и
так, чтобы
.
Тогда
.
Подставляя
,
,
в , получим
или
.
Выражения, стоящие в первых двух скобках, обращаются в нуль, так как у1 и у2 – решения однородного уравнения. Следовательно, последнее равенство имеет вид
.
Объединяя уравнения и , получаем для определения производных от неизвестных функций и систему:
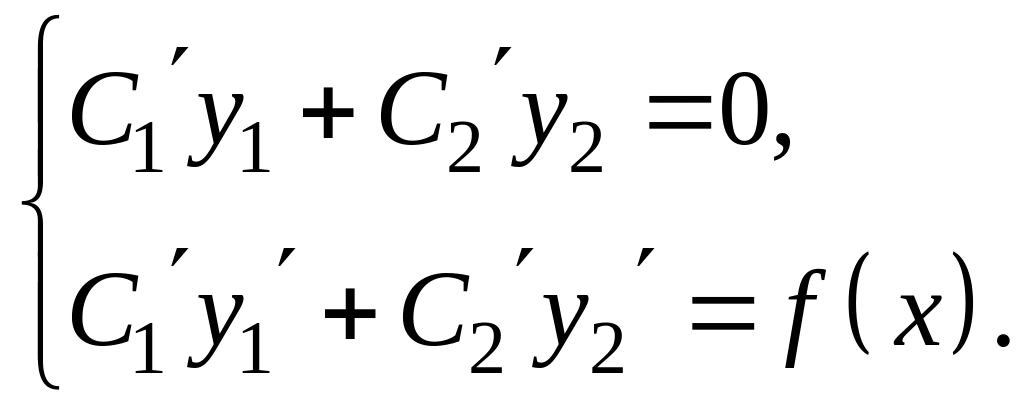
Определитель этой
системы
,
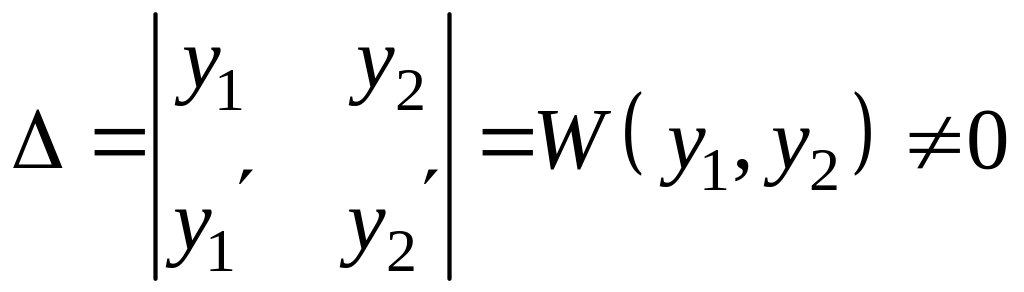так как у1
и у2
– линейно независимые решения. Поэтому
система имеет единственное решение.
Решая ее, найдем
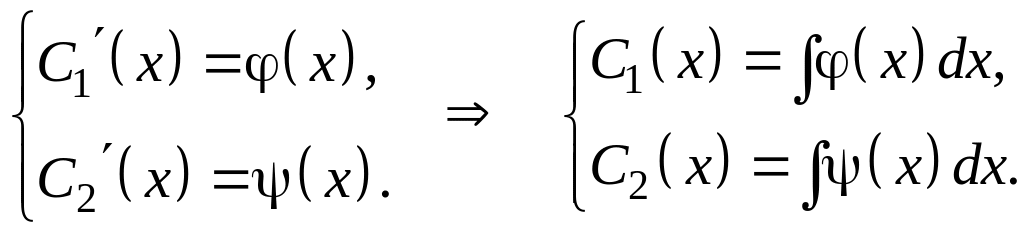(так как мы ищем частное решение, то
постоянные интегрирования не берем).
Подставляя полученные функции и в , получим частное решение.
Пример
9.17.1. Найти
общее решение уравнения
.
Решение. Найдем общее решение однородного уравнения
.
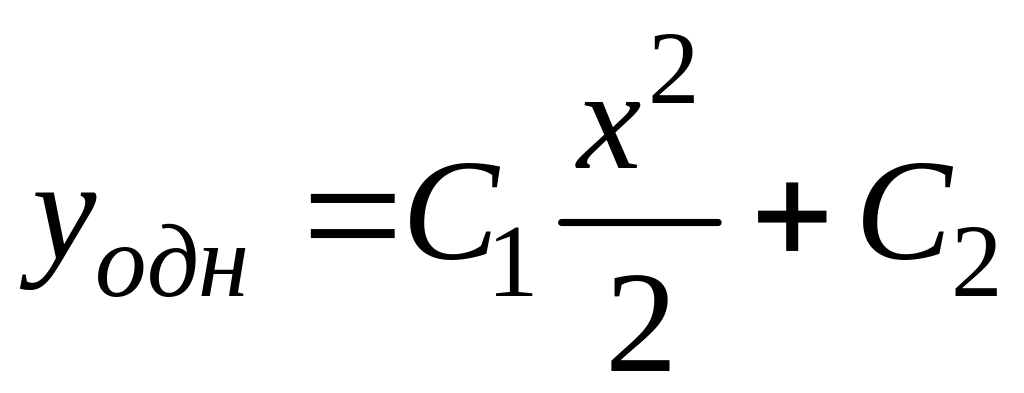Частное решение неоднородного уравнения ищем в виде
(
,
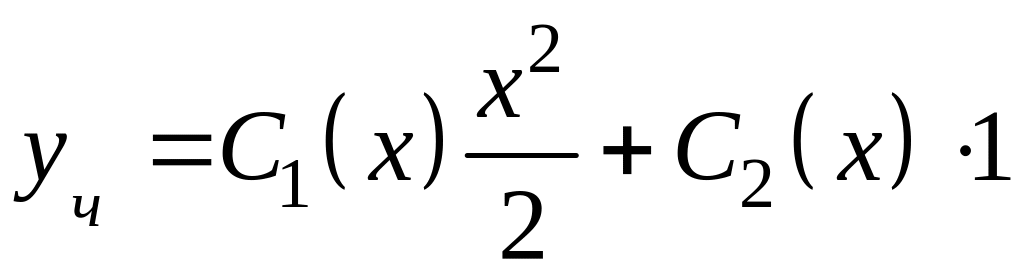
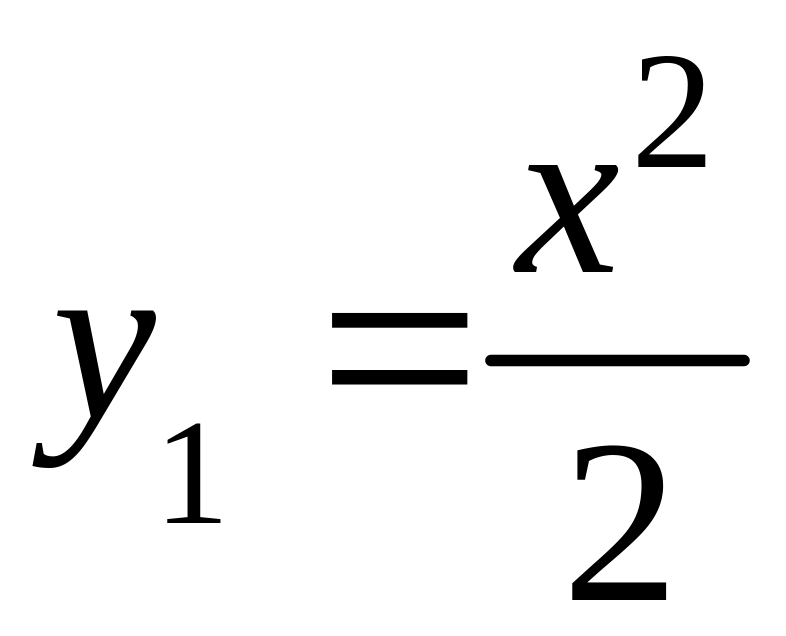– частные решения однородного уравнения).
Составляем систему
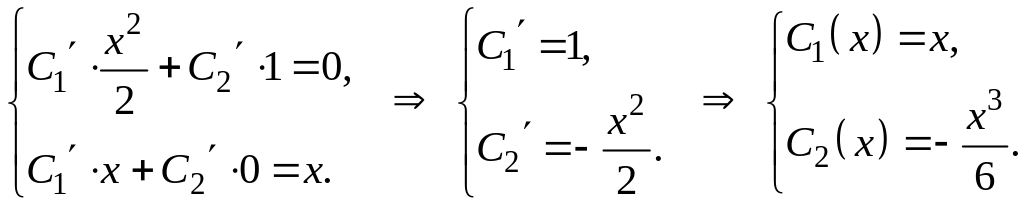
Тогда
,
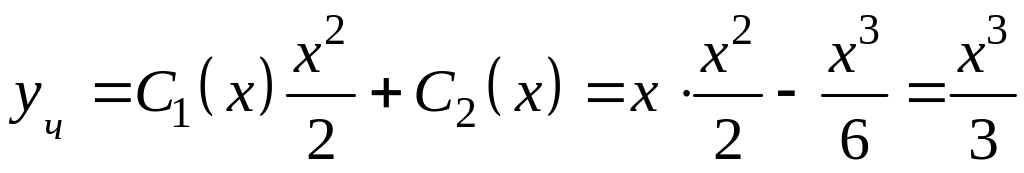а общее решение
.
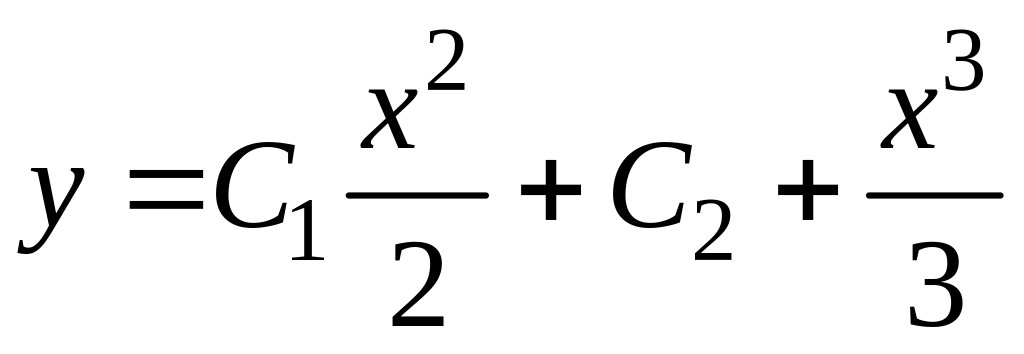При отыскании частных решений иногда полезно использовать следующую теорему.
Теорема 9.17.2. Частное решение уравнения
,
где правая часть
есть сумма двух функций
и
,
можно представить в виде суммы
,
где
и
– частные решения, соответственно,
уравнений
,
.
Упражнение. Доказать теорему самостоятельно.
Для уравнения третьего порядка
,
,
а система выглядит следующим образом
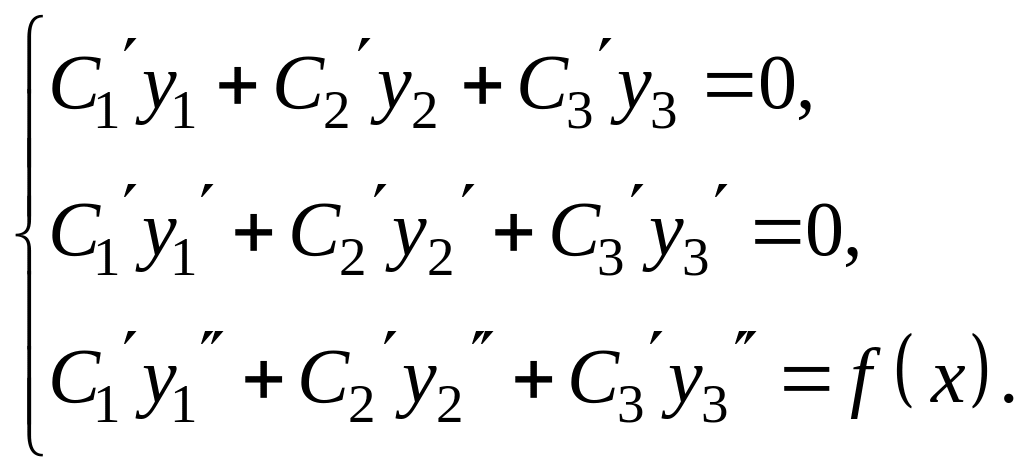
Аналогично можно найти частное решение и для уравнений более высокого порядка.
9.18. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Рассмотрим дифференциальное уравнение с постоянными коэффициентами
,
где p и q – постоянные действительные числа.
В предыдущем разделе был указан общий метод нахождения частного решения неоднородного уравнения (метод вариации). В случае уравнения с постоянными коэффициентами частное решение иногда (для так называемых «специальных» правых частей) бывает возможным найти проще, не прибегая к интегрированию.
Рассмотрим такие случаи для уравнения .
Пусть правая часть этого уравнения представляет собой произведение показательной функции на многочлен, т.е.
,
где
– известный многочлен n-ой
степени. Тогда возможны следующие
случаи:
Число не является корнем характеристического уравнения
.
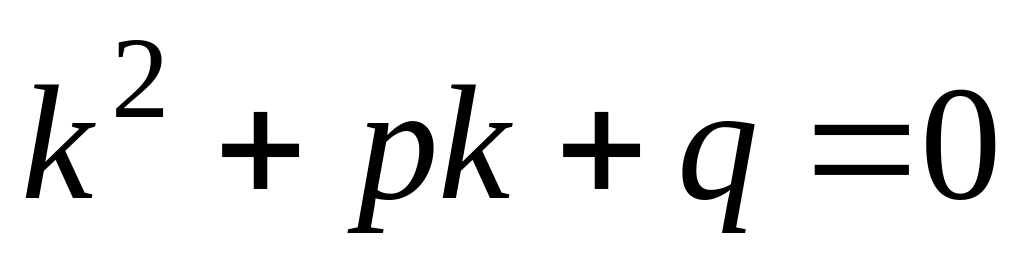В этом случае частное решение нужно искать в виде
,
где
– многочлен тоже степени n
(как и многочлен
)
с неизвестными коэффициентами А0,
А1,
…, An.
Тогда
,
.
Подставляя
,
и
в , получаем
.
Сокращая на
и группируя, имеем
,
где
– многочлен n-ой
степени,
– многочлен степени (n1),
– многочлен степени (n2).
Таким образом, слева и справа от знака
равенства в стоят многочлены n-ой
степени. Приравнивая коэффициенты при
одинаковых степенях х
(число неизвестных коэффициентов равно
n+1),
получим систему из (n+1)
уравнений. Решив эту систему, найдем
неизвестные коэффициенты А0,
А1,
…, An.
Число есть простой (однократный) корень характеристического уравнения, т.е.
.
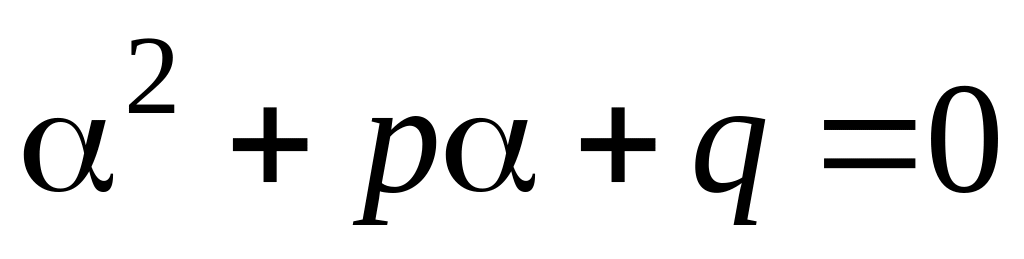Если в этом случае частное решение искать в виде , то в равенстве слева получится многочлен (n1) степени, так как и слагаемое с вообще исчезает. Следовательно, ни при каких А0, А1, …, An равенство не будет тождеством. Поэтому частное решение надо искать в виде многочлена (n+1)-й степени, но без свободного члена (который исчез бы при дифференцировании). Степень многочлена увеличим на 1 умножением на х, т.е.
.
Число есть двукратный корень характеристического уравнения
.
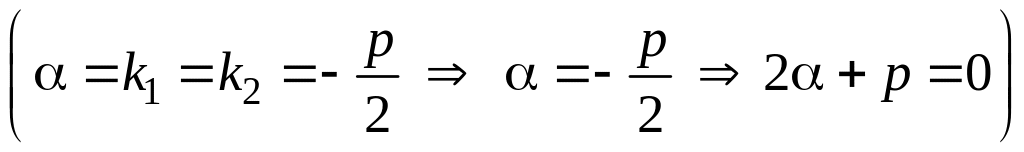Тогда в равенстве
и
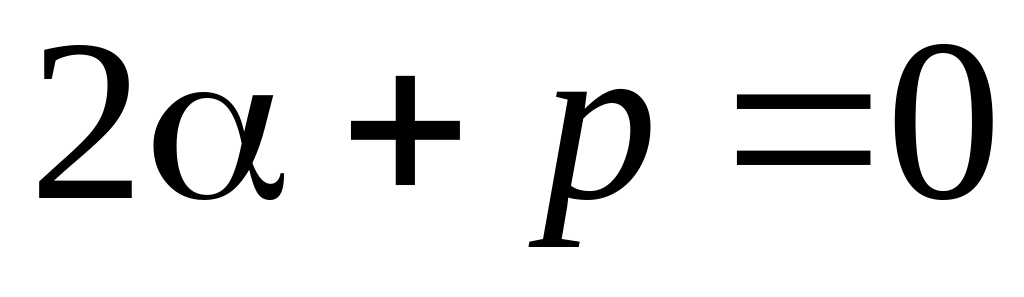и оно примет вид
,
т.е. в левой части многочлен (n2) степени, поэтому степень многочлена надо увеличить на 2, это можно сделать умножением на х2 (свободный член и коэффициент при х исчезают при двукратном дифференцировании), т.е.
.
Все три случая
можно объединить одной формулой
,
где е
– кратность ,
как корня характеристического уравнения.
Пример 9.18.1. Найти общее решение уравнения
.
Решение. Характеристическое
уравнение для соответствующего
однородного уравнения
имеет вид
.
= 0,
= 3, и поэтому общее решение
.
Правая часть
,
где
= 3 не является корнем характеристического
уравнения. Поэтому частное решение
неоднородного уравнения ищем в виде
,
или
,
.
Подставляя , , в исходное уравнение, получим
.
Сокращая на
обе части уравнения и приводя подобные
члены, имеем
.
Приравнивая коэффициенты при одинаковых степенях х слева и справа от знака равенства, получим систему для определения неизвестных коэффициентов А, В, С.
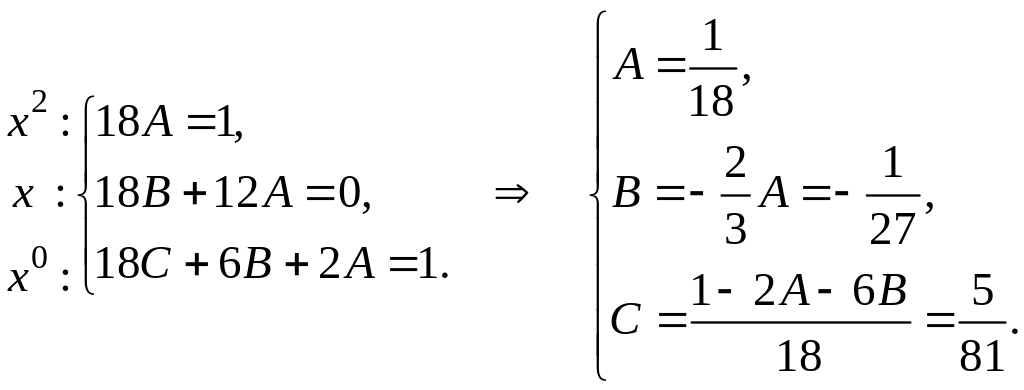
Следовательно,
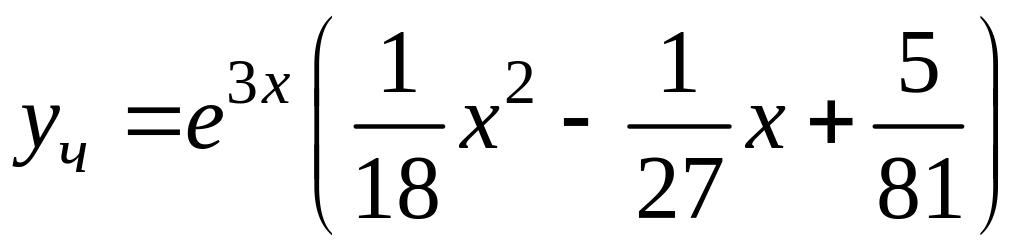частное решение
,
а общее решение
.
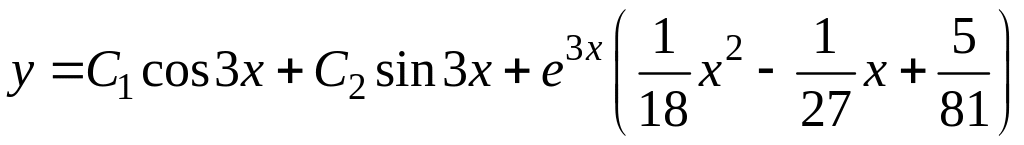Пример
9.18.2. Решить
уравнение
.
Решение. 
,
и
.
,
где
= 1 является однократным корнем
характеристического уравнения
,
поэтому
,
т.е
,
,
.
Подставим , и в исходное уравнение
.
Сокращая на обе части и приводя подобные члены, получим
.
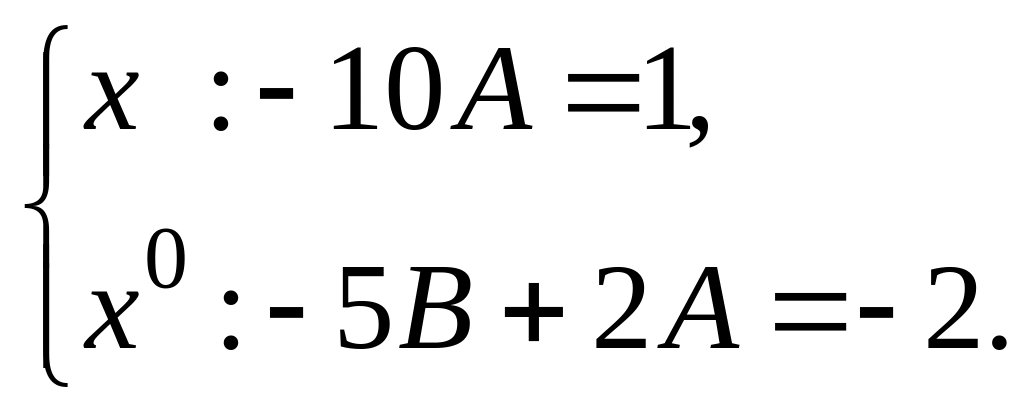
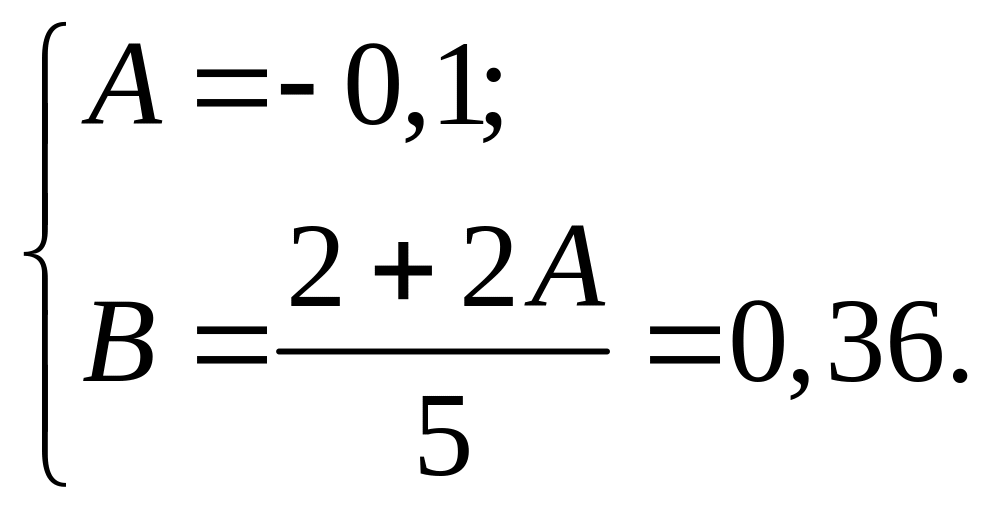
Следовательно,
,
а общее решение
.
Пусть правая часть имеет вид
,
где
и
– многочлены от х.
Составим
комплексно-сопряженные числа
,
где
берется из показателя
,
а
из аргумента cos
x
и sin
x,
и рассмотрим два случая:
если числа не являются корнями характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде
,
где u(x) и v(x) – многочлены, степень которых равна наивысшей степени многочленов и .
если числа являются корнями характеристического уравнения, то
.
При этом указанные формы частных решений и сохраняются в полном виде и в том случае, когда в правой части один из многочленов или отсутствует.
Пример
9.18.3. Решить
уравнение
.
Решение.
.
Правая часть
,
где
= 2,
= 1,
,
.
не являются корнями
характеристического уравнения, поэтому
,
т.е.
или
,
.
Подставляем , и в исходное уравнение
.
Сокращая обе части
на
и приводя подобные члены, получим
, или
.
Приравнивая коэффициенты при cos x и sin x в левой и правой части равенства, имеем
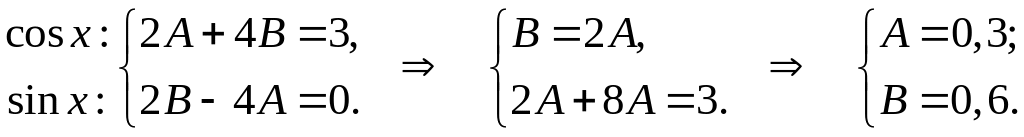
Следовательно,
частное решение
,
а общее
.
Рассмотрим далее важный частный случай. Пусть правая часть имеет вид:
,
где M и N – постоянные числа.
Если
(
= 0) не являются корнями характеристического
уравнения, то частное решение следует
искать в виде:
.
Если являются корнями характеристического уравнения, то частное решение следует искать в виде:
.
Пример
9.18.4. Найти
общее решение
.
Решение. Характеристическое
уравнение
имеет корни
.
не являются корнями
характеристического уравнения, поэтому
частное решение ищем в виде 
,
где А
и В
– неизвестные коэффициенты, подлежащие
определению.
,
.
Подставляя
,
и
в исходное уравнение получим:
.
Приравнивая коэффициенты при cos x и sin x, получим:
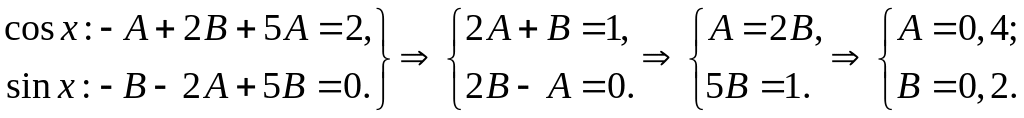
Общее решение
,
т.е.
.
Пример 9.18.5. Указать вид частного решения уравнения
.
Решение. 
,
.
Из cos
2x
= 2.
2i совпадают с корнями характеристического уравнения, поэтому частное решение исходного уравнения следует искать в виде
.
В случае неоднородных дифференциальных уравнений высшего порядка с постоянными коэффициентами со специальной правой частью частные решения находятся аналогично.
Пример
9.18.6. Решить
уравнение
.
Решение. Характеристическое
уравнения
,
;
,
.
Из правой части
= 0
не является корнем характеристического
уравнения, поэтому
,
т.е.
.
Тогда
,
,
,
.
,
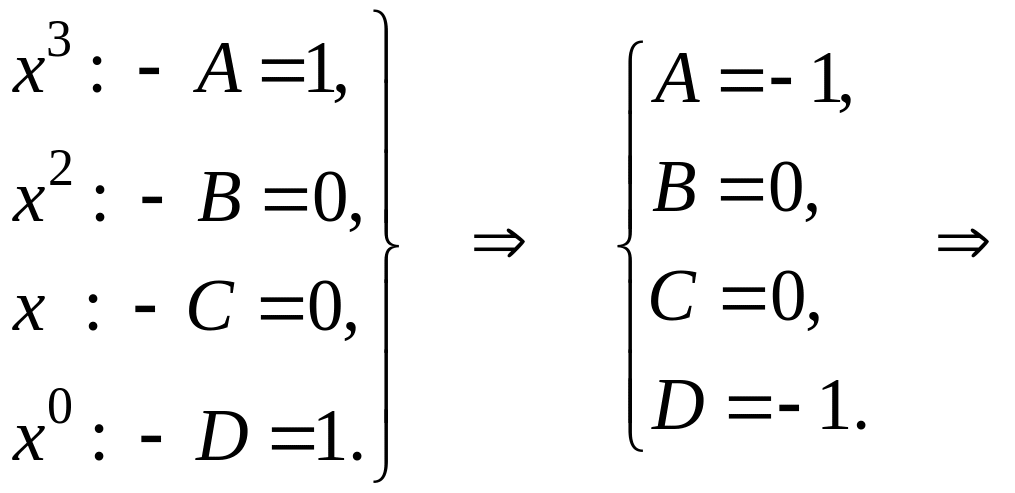
а общее решение
.
Пример 9.18.7. Указать вид частного решения уравнения
.
Решение.
,
.
Из правой части
являются корнями характеристического
уравнения, поэтому частное решение ищем
в виде: 
.