- •5. Квантова фізика
- •5.1. Квантові властивості випромінювання Довідковий матеріал
- •5.1.1. Енергія, імпульс і маса фотона
- •5.1.2. Фотоелектричний ефект
- •5.1.3. Тиск світла
- •5.2. Гальмівне ренгенівське випромінювання. Ефект Комптона Довідковий матеріал
- •5.3. Закони теплового випромінювання Довідковий матеріал
- •5.4. Хвильові властивості речовини Довідковий матеріал
- •5.4.1. Хвилі де Бройля
- •5.4.2. Принцип невизначеності Гейзенберга
- •5.4.3. Рівняння Шредінгера. Мікрочастинка в потенціальній ямі. Проходження мікрочастинки через потенціальний бар’єр
- •5.5. Модель атома Резерфорда-Бора Довідковий матеріал
- •5.6. Квантові явища у твердих тілах Довідковий матеріал
- •5.6.1. Класична теорія теплоємності
- •5.6.2. Теорія теплоємності Ейнштейна
- •5.6.3. Теорія теплоємності Дебая
- •5.6.4. Електрони в металі. Розподіл Фермі−Дірака
- •5.7. Фізика атомного ядра Довідковий матеріал
- •5.7.1. Будова атомних ядер. Дефект маси й енергія зв’язку атомних ядер
- •5.7.2. Закон радіоактивного розпаду
- •5.7.3. Ядерні реакції
- •Елементарні частинки Довідковий матеріал
Елементарні частинки Довідковий матеріал
Повна енергія релятивіської частинки:
Е = m0c2 + Ек,
де m0c2− енергія спокою частинки, Ек − кінетична енергія частинки.
Закон збереження енергії для ядерних реакцій:
Σm0c2 + ΣЕк=Σ m′0c2 +ΣЕ′к ,
де Σm0c2 та Σ m′0c2 − відповідно сума енергій спокою частинок до та після реакції, ΣЕк та ΣЕ′к − сума кінетичних енергій частинок до й після реакції.
Імпульс релятивіської частинки:
 .
.
При розгляді зіткнення частинок часто використовують інваріантну величину:
Е2
− р2с2
=
![]() ,
де
Е
і р
− повна енергія й імпульс системи,
m0−
маса
спокою утвореної частинки.
,
де
Е
і р
− повна енергія й імпульс системи,
m0−
маса
спокою утвореної частинки.
Значення порогової кінетичної енергії для налітаючої частинки т1 на частинку-мішень т2:
 ,
де
,
де
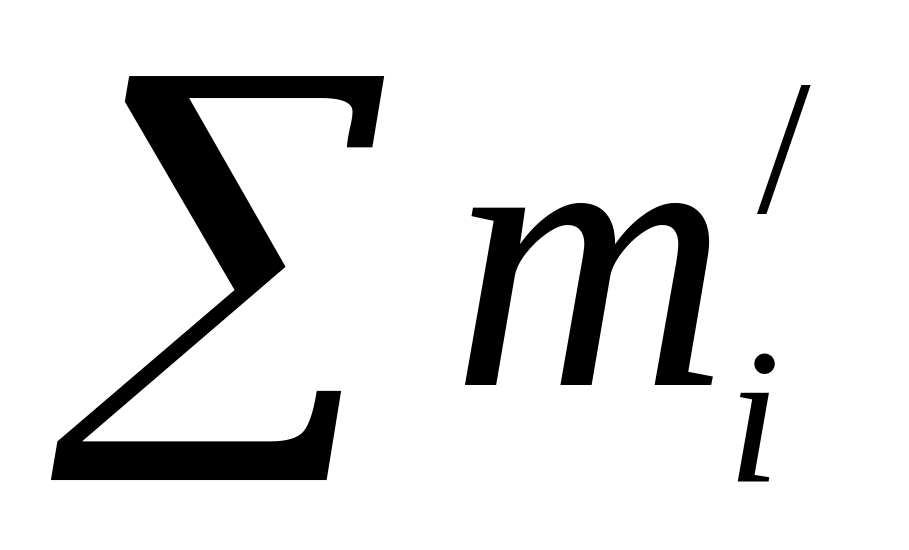 – сума мас частинок, утворених в
результаті реакції.
– сума мас частинок, утворених в
результаті реакції.
Задачі
Розганяючись прискорювальним полем у бетатроні, електрон набуває кінетичної енергії 0,8 МеВ. Яку швидкість має електрон? [2,75∙108 м/с].
Знайти швидкість протона, який у прискорювальному полі пройшов різницю потенціалів 500 МВ. [2,1∙108 м/с].
Знайти сумарну кінетичну енергію всіх частинок, які виникають у процесі розпаду вільного нейтрона за схемою: n → p + e−+
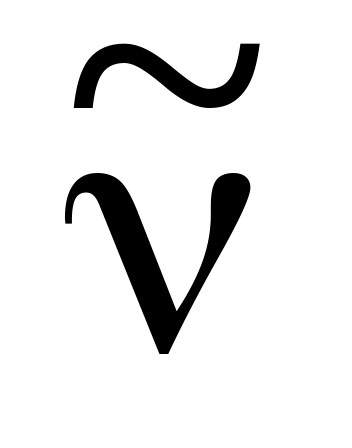 .
Кінетичну енергію нейтрона і масу
спокою антинейтрино можна не враховувати.
[0,77 МеВ].
.
Кінетичну енергію нейтрона і масу
спокою антинейтрино можна не враховувати.
[0,77 МеВ].Показати, що народження пари електрон−позитрон одним квантом можливе тільки в тому разі, коли в реакції бере участь частинка з масою спокою m ≠ 0. [(Е+m1c2)2−p2c2=(m1=2m)2c4, де p=E/c (після взаємодії вихідні частинки знаходяться в стані спокою на порозі реакції). Рівність не виконується при m1=0].
Фотони з енергіями в 1,51 МеВ взаємодіють між собою з утворенням пари електрон−позитрон за схемою:
 .
Яку швидкість будуть мати утворені
електрон і позитрон?
[2,82∙108 м/с].
.
Яку швидкість будуть мати утворені
електрон і позитрон?
[2,82∙108 м/с].Покажіть, що при зіткненні фотона з вільним електроном він не може передати йому всю свою енергію. [Нехай фотон передає енергію електрону, тоді
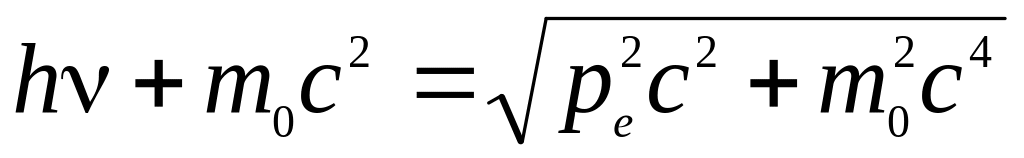 .
Звідки
.
Звідки
 ,
що протирічить
закону збереження імпульсу].
,
що протирічить
закону збереження імпульсу].У камеру Вільсона, яка міститься в однорідному магнітному полі з індукцією 5 Тл, влітає електрон з кінетичною енергією 150 МеВ і залишає слід у вигляді дуги кола. Знайти радіус кривизни траєкторії електрона. [12,9 см].
При співударі електрона й позитрона з однаковими кінетичними енергіями 0,3 МеВ вони перетворюються у два однакових фотони. Чому дорівнює енергія утворених фотонів та яка довжина хвилі в них? [0,812 МеВ; 1,53 пм].
Середня швидкість зміни магнітного потоку в бетатроні на 80 МеВ складає 60 Вб/с. Визначити: 1) число обертів електрона орбітою за час прискорення; 2) шлях, пройдений електроном, якщо радіус орбіти дорівнює 0,3 м; 3) час прискорення. [1) 1,33∙106 обертів; 2) 2,5∙103 км; 3) 0,0083 с].
Позитрон з кінетичною енергією 0,75 МеВ налітає на вільний електрон, що перебуває у стані спокою. У результаті анігіляції виникає два γфотони з однаковими енергіями. Визначити кут φ між напрямками їхнього розлітання. [98о54/].
У циклотроні з радіусом дуантів 0,8 м та індукцією поля 1,5 Тл прискорюються протони. Визначити: 1) максимальну кінетичну енергію, якої набувають протони; 2) частоту генератора, який живить циклотрон (часом проходження протонами прискорювального проміжку знехтувати). [1) 68 МеВ; 2) 2,29∙107 Гц].
Фотон з енергією 3,02 МеВ у полі важкого ядра перетворився в пару електрон−позитрон. Беручи, що кінетична енергія частинок однакова, визначити кінетичну енергію кожної частинки. [0,998 МеВ].
Схема розпаду π0-мезона під час руху: π0→ γ + γ. Знайти кут між напрямками розлітання γквантів, якщо їхні енергії Е1 та Е2, а маса спокою π0-мезона дорівнює m0. [
 ].
].
Елементарна частинка -мезон (
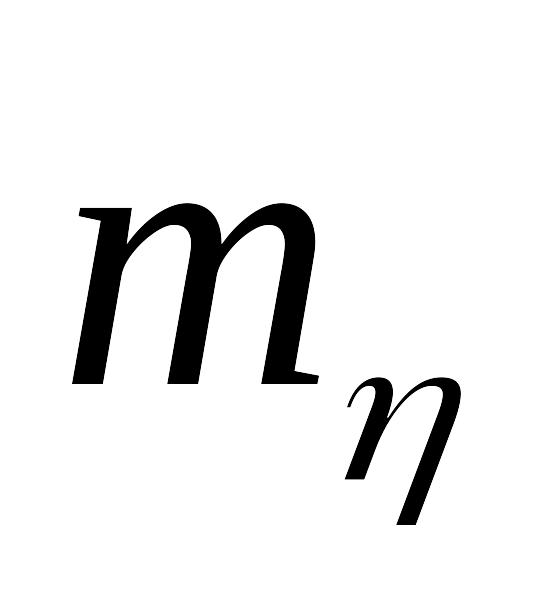 =0,589372
а.о.м.), розпадаючись,
перетворюється у два однакових
-фотони.
Визначте енергію та довжину хвилі
-фотонів.
Кінетичну енергію і імпульс
-мезона
можна не враховувати. [
=
274,5 МеВ;
=
4,53 фм].
=0,589372
а.о.м.), розпадаючись,
перетворюється у два однакових
-фотони.
Визначте енергію та довжину хвилі
-фотонів.
Кінетичну енергію і імпульс
-мезона
можна не враховувати. [
=
274,5 МеВ;
=
4,53 фм].Бомбардуючи пучком заряджених
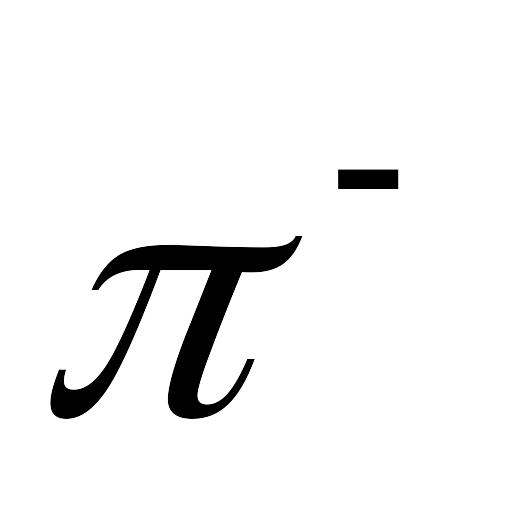 -мезонів
нерухому водневу мішень, одержують
-мезонів
нерухому водневу мішень, одержують
 -гіперони
і нейтральні
-гіперони
і нейтральні
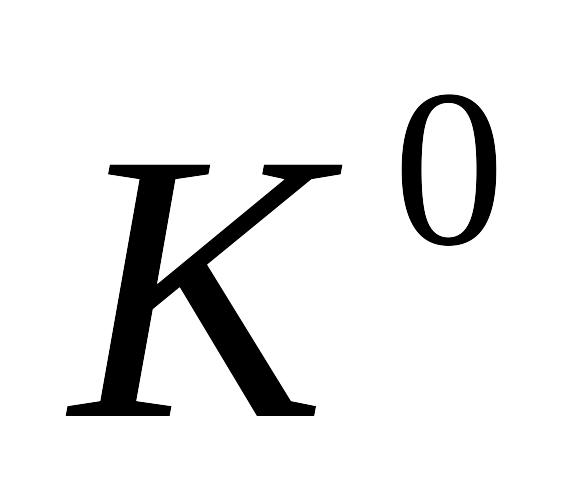 -мезони
за схемою:
-мезони
за схемою:
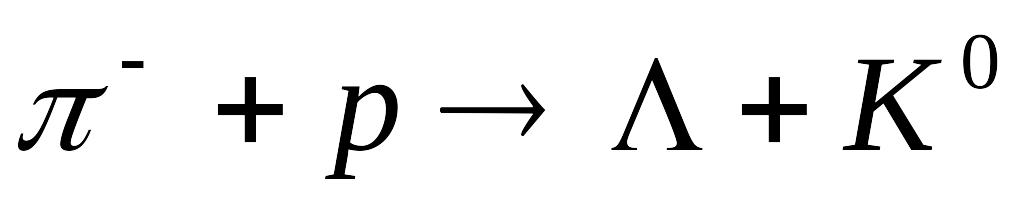 .
Визначте порогову енергію цієї реакції.
Врахуйте, що маси спокою
.
Визначте порогову енергію цієї реакції.
Врахуйте, що маси спокою
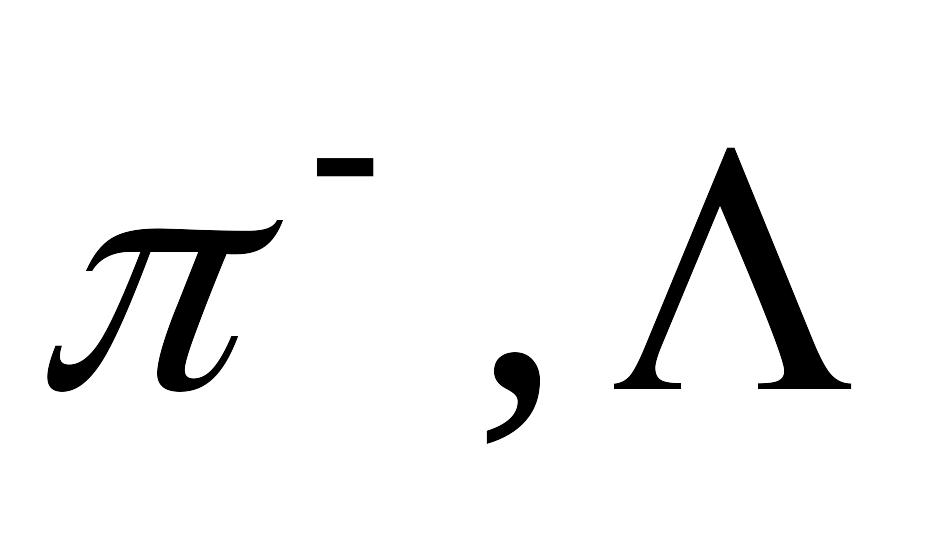 і
-частинок
відповідно дорівнюють: 0,1449275 а.о.м.,
1,1980676 а.о.м. і 0,53462158 а.о.м. [768,7
МеВ].
і
-частинок
відповідно дорівнюють: 0,1449275 а.о.м.,
1,1980676 а.о.м. і 0,53462158 а.о.м. [768,7
МеВ].У циклотроні під дією магнітного поля і різниці потенціалів між дуантами в 30 кВ, -частинки прискорюються до енергії 50 МеВ. Скільки обертів за час прискорення в циклотроні встигають зробити -частинки? На скільки відсотків збільшується маса -частинки перед вильотом з циклотрону відносно маси її спокою? [N= 416 обертів; маса збільшилася на 1,34%].
Схема розпаду нейтрального
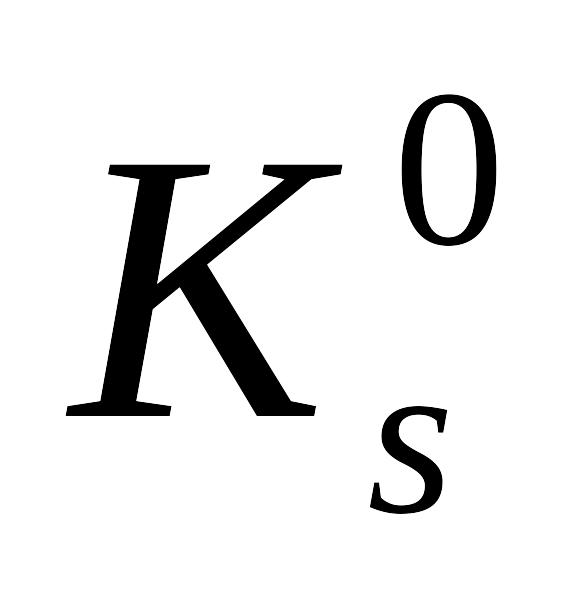 -мезона
на два однакових
-мезона
на два однакових
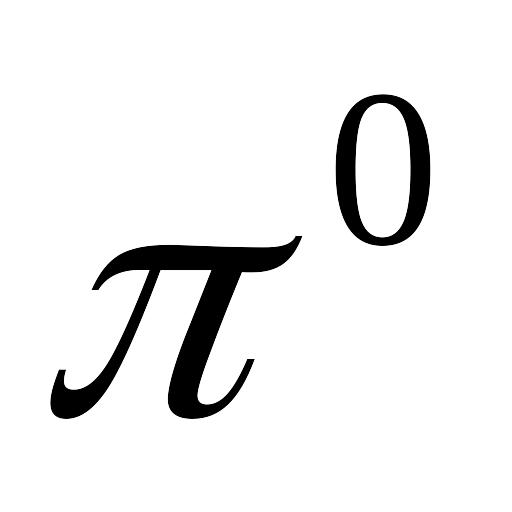 -мезони
відбувається за схемою:
-мезони
відбувається за схемою:
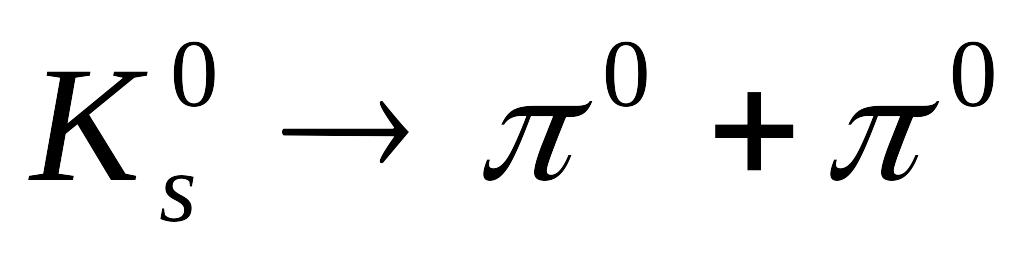 .
Визначте кут між напрямами розлітання
нейтральних
-мезонів,
якщо маси спокою
і
-мезонів
відповідно дорівнюють 0,5346216 а.о.м. і
0,1449275 а.о.м. Кінетичну енергію і імпульс
-мезона
можна не враховувати. [
.
Визначте кут між напрямами розлітання
нейтральних
-мезонів,
якщо маси спокою
і
-мезонів
відповідно дорівнюють 0,5346216 а.о.м. і
0,1449275 а.о.м. Кінетичну енергію і імпульс
-мезона
можна не враховувати. [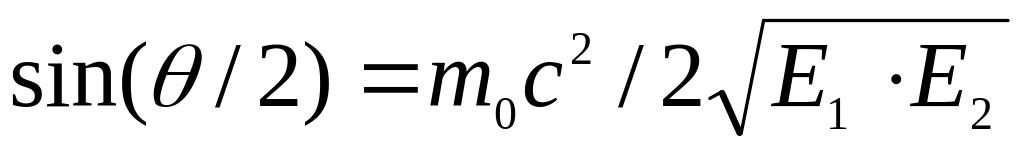 ;
;
 ].
].Визначте власний час життя
 -гіперонів,
які в нерухомій системі відліку
пролітають від місця свого народження
до місця розпаду відстань l=
0,70 м. Маса спокою і кінетична енергія
цих частинок відповідно дорівнюють
-гіперонів,
які в нерухомій системі відліку
пролітають від місця свого народження
до місця розпаду відстань l=
0,70 м. Маса спокою і кінетична енергія
цих частинок відповідно дорівнюють
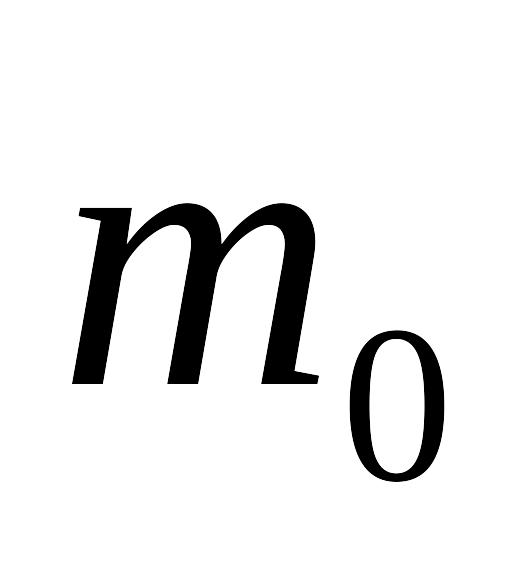 =2,3434
=2,3434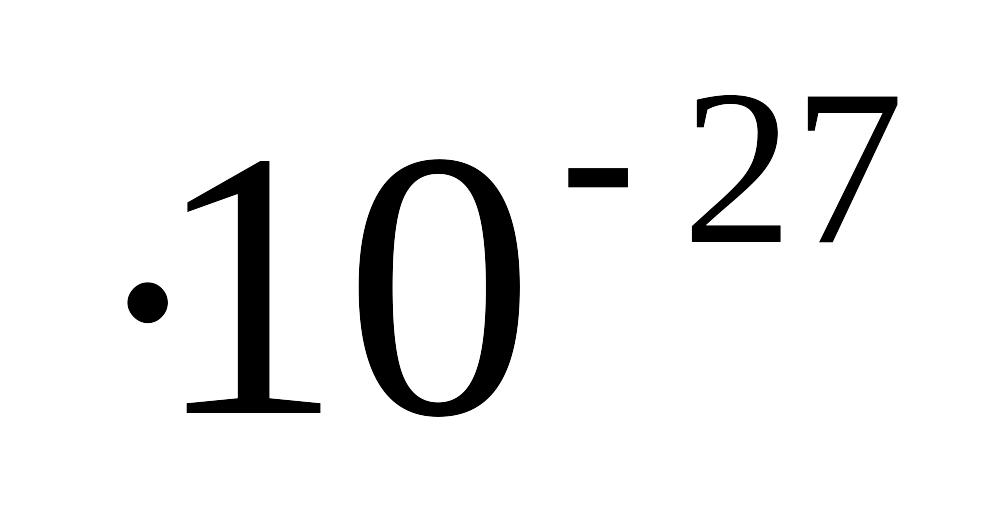 кг
і Т=
9 ГеВ. [
кг
і Т=
9 ГеВ. [ =
= c].
c].
Визначте поріг фотонародження зарядженого
 -мезона
на нуклоні за такою схемою:
-мезона
на нуклоні за такою схемою:
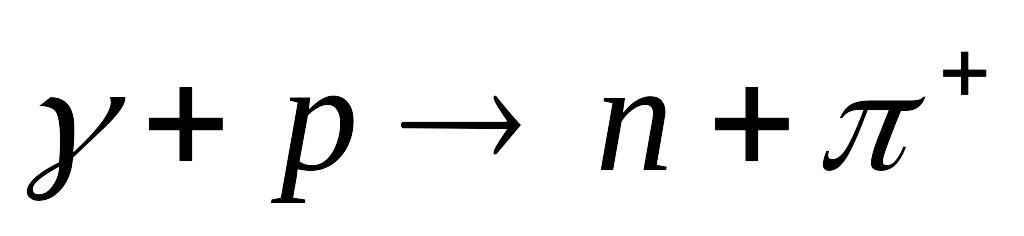 .
Врахуйте, що маса спокою
-мезона
дорівнює 0,1502952 а.о.м. [
.
Врахуйте, що маса спокою
-мезона
дорівнює 0,1502952 а.о.м. [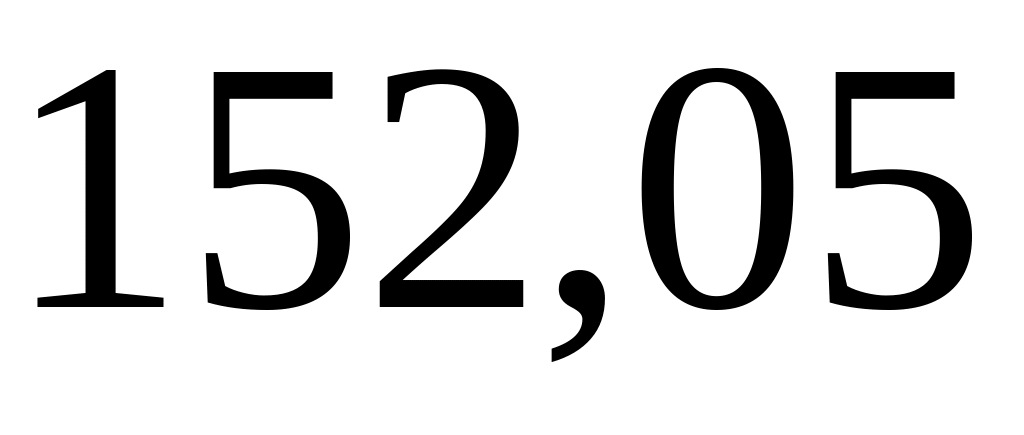 МеВ.]
МеВ.]Власний час життя -мезонів, які розпадаються за схемою
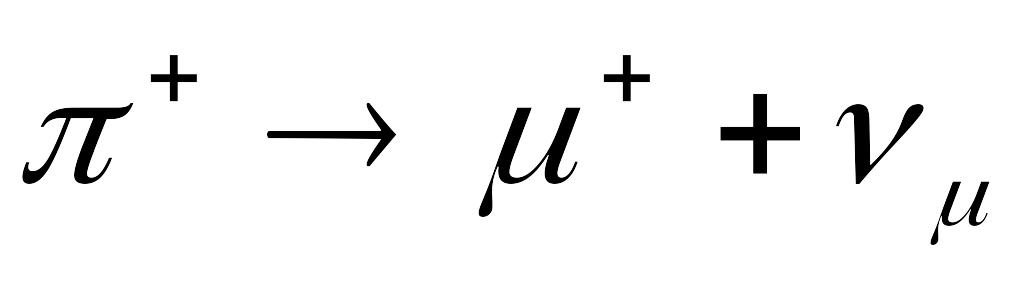 ,
дорівнює
,
дорівнює
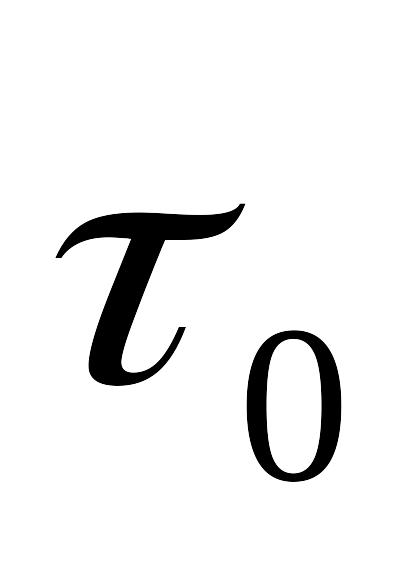 =
2,6
=
2,6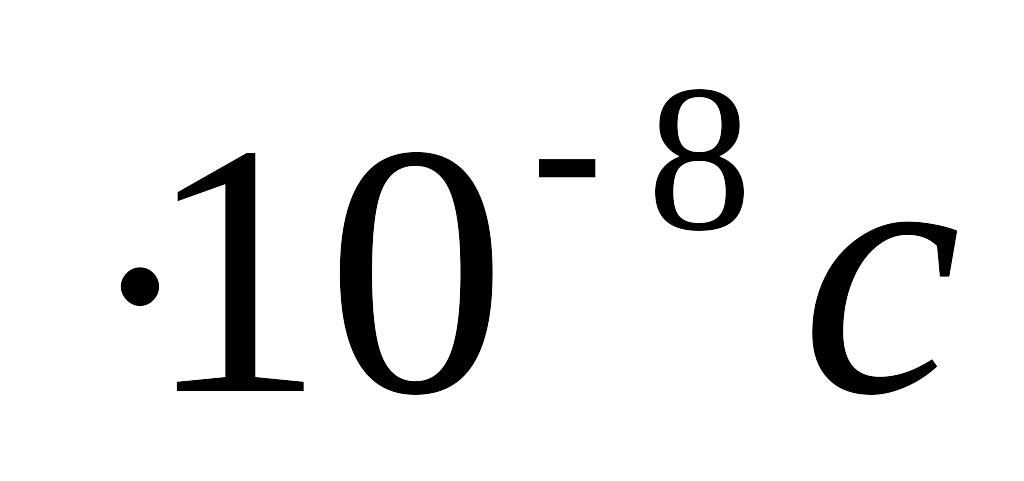 .
Яку середню відстань пролітають ці
мезони у нерухомій системі відліку
від місця народження до точки їх
розпаду, якщо їх кінетична енергія Т=
852,6 МеВ, а маса спокою
=
0,24889∙10−27кг.
[
.
Яку середню відстань пролітають ці
мезони у нерухомій системі відліку
від місця народження до точки їх
розпаду, якщо їх кінетична енергія Т=
852,6 МеВ, а маса спокою
=
0,24889∙10−27кг.
[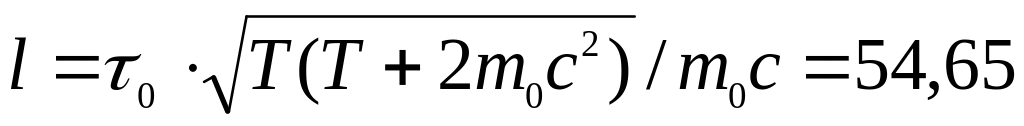 м].
м].Під впливом слабких взаємодій
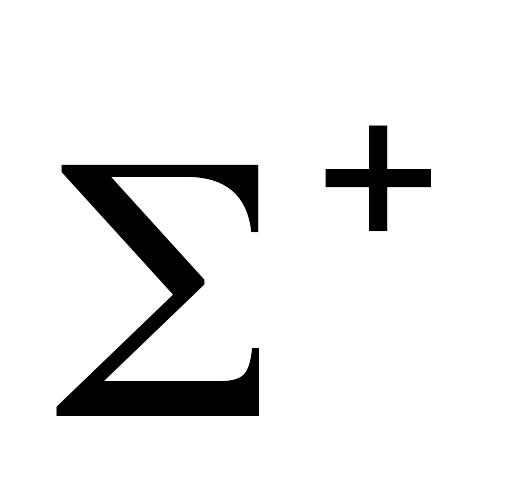 -гіперон
розпадається за схемою:
-гіперон
розпадається за схемою:
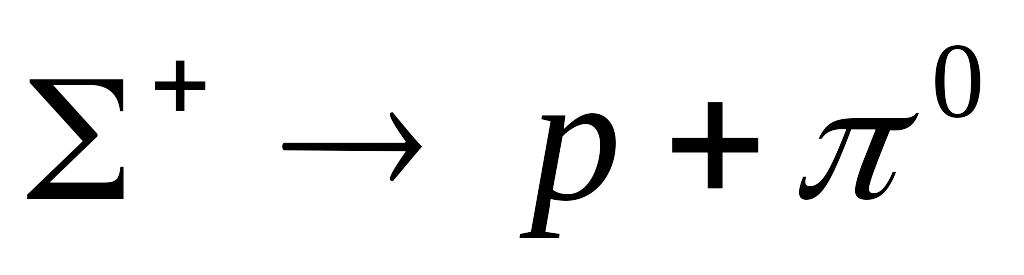 .
Якою кінетичною енергією володітимуть
як протон, так і
-мезон?
Врахуйте, що маси спокою
-гіперона
і
-мезона
відповідно дорівнюють 1,27643586 а.о.м. і
0,1449275 а.о.м. Кінетичну енергію й імпульс
-гіперона
можна не враховувати. [
.
Якою кінетичною енергією володітимуть
як протон, так і
-мезон?
Врахуйте, що маси спокою
-гіперона
і
-мезона
відповідно дорівнюють 1,27643586 а.о.м. і
0,1449275 а.о.м. Кінетичну енергію й імпульс
-гіперона
можна не враховувати. [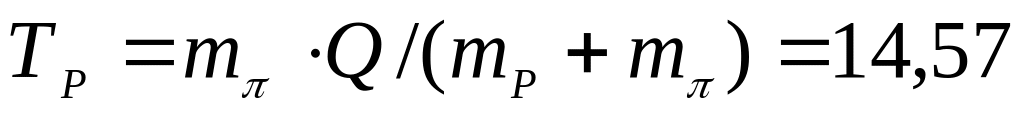 МеВ;
МеВ; =101,23
МеВ]ю
=101,23
МеВ]юВизначте порогову кінетичну енергію бомбардуючого протона в реакції народження пари нуклон-антинуклон
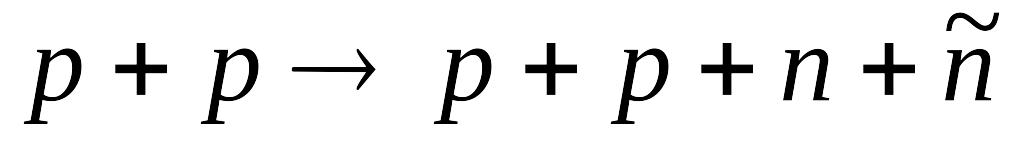 .
[5,64 ГеВ].
.
[5,64 ГеВ].
У сучасному синхрофазотроні з жорстким фокусуванням протони прискорюють до кінетичної енергії Т= 76 ГеВ. У скільки разів збільшується релятивістська маса протонів на виході із синхрофазотрона порівняно із його масою спокою? [82 рази].
Володіючи кінетичною енергією в = 1,551 разів більшою за енергію спокою, -гіперон пролітає в нерухомій системі відліку від місця народження до точки розпаду за схемою
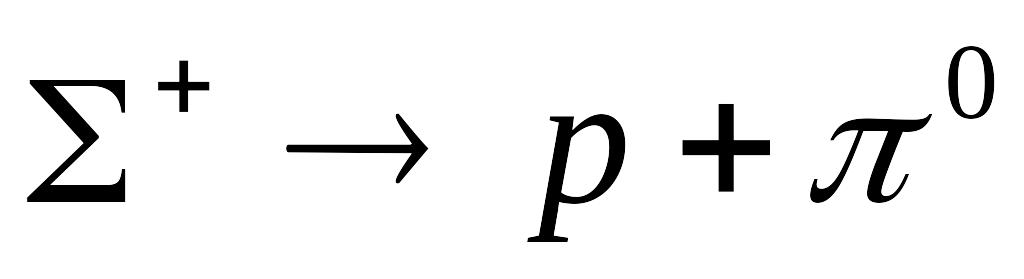 відстань 5,63 см.
Визначте середній час руху гіперона
в нерухомій системі відліку, прийнявши,
що його маса спокою
=
2,11378
кг.
[
відстань 5,63 см.
Визначте середній час руху гіперона
в нерухомій системі відліку, прийнявши,
що його маса спокою
=
2,11378
кг.
[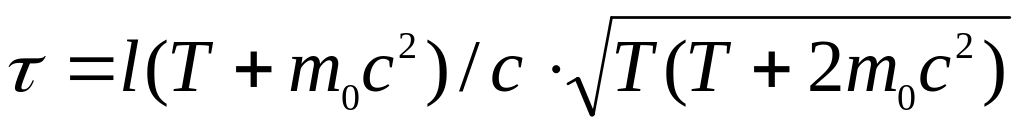 =
2,04
=
2,04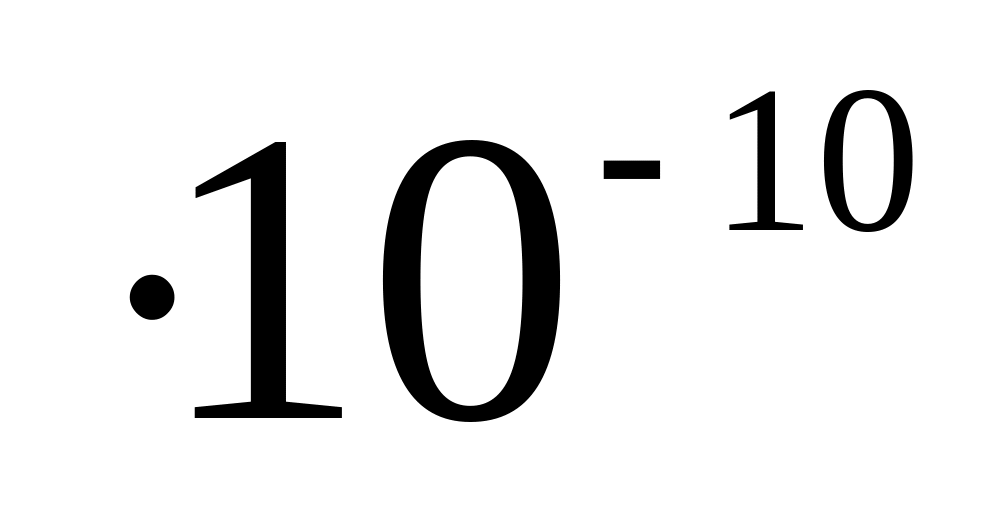 c].
c].Для одержання -гіперонів використовують реакцію зіткнення протон-протон за схемою
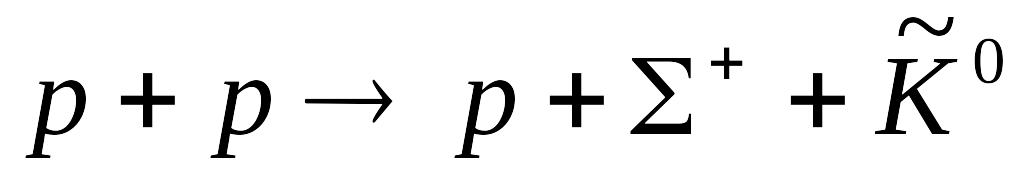 .
Встановіть, які саме закони збереження
дотримані в цій реакції? Визначте
мінімальну кінетичну енергію налітаючого
протона, необхідну для здійснення
вказаної реакції. Врахуйте, що маси
спокою
і
частинок відповідно дорівнюють
1,27643586 а.о.м. і 0,53462158 а.о.м. [1,796
ГеВ].
.
Встановіть, які саме закони збереження
дотримані в цій реакції? Визначте
мінімальну кінетичну енергію налітаючого
протона, необхідну для здійснення
вказаної реакції. Врахуйте, що маси
спокою
і
частинок відповідно дорівнюють
1,27643586 а.о.м. і 0,53462158 а.о.м. [1,796
ГеВ].Нейтральний -мезон, розпадаючись, перетворюється на три однакових нейтральні -мезони. Визначте кінетичну енергію кожної з частинок, що утворились після розпаду. Маси спокою -мезона і -мезона відповідно дорівнюють 0,589372 а.о.м. і 0,1449275 а.о.м. Кінетичну енергію й імпульс -мезона можна не враховувати. [48 МеB].
У фазотроні з радіусом дуантів 3 м протони розганяють до енергії 680 МеВ. Визначте індукцію магнітного поля в фазотроні. У скільки разів маса протонів в кінці прискорення у фазотроні буде більшою за його масу спокою? [1,26 Тл;
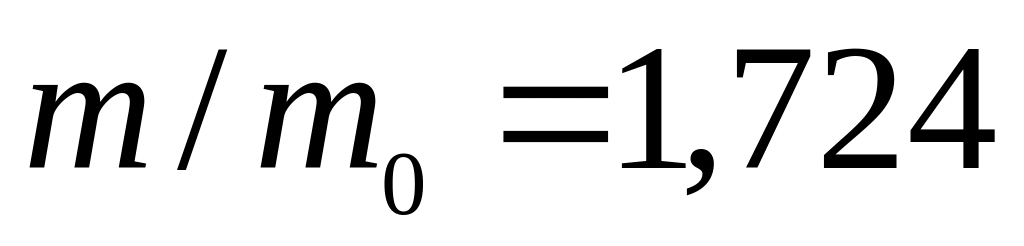 ].
].
Визначте порогову кінетичну енергію бомбардуючих протонів в реакції одержання трьох нуклон-антинуклонних пар (
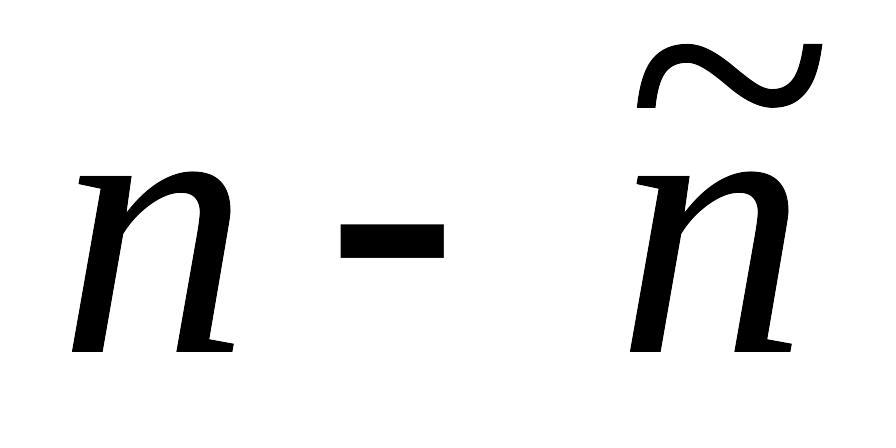 )
за схемою
)
за схемою
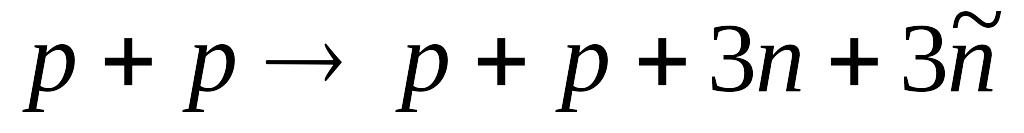 .
[28,213
ГеВ].
.
[28,213
ГеВ].Яку відстань пролітають
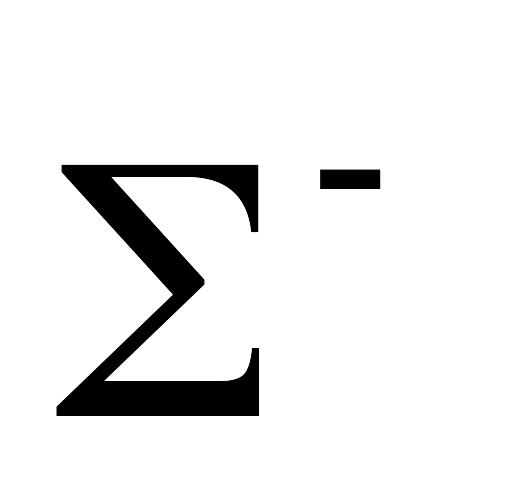 -гіперони
від місця народження до точки розпаду
в нерухомій системі відліку, якщо їх
власний час життя
=
1,5∙10−10
c.
Прийняти до уваги, що маса спокою цих
частинок
=
2,13314∙10−27
кг, а кінетична енергія дорівнює
8,85 ГеВ.
[0,38
м].
-гіперони
від місця народження до точки розпаду
в нерухомій системі відліку, якщо їх
власний час життя
=
1,5∙10−10
c.
Прийняти до уваги, що маса спокою цих
частинок
=
2,13314∙10−27
кг, а кінетична енергія дорівнює
8,85 ГеВ.
[0,38
м].Яку порогову кінетичну енергію повинні мати бомбардуючі -мезони в реакції за схемою
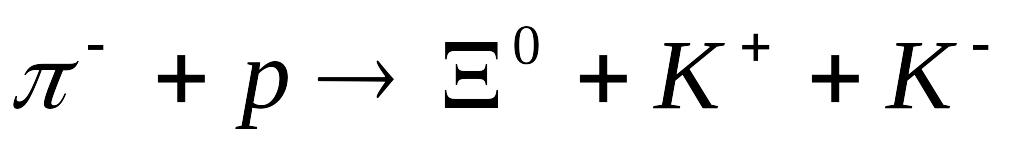 ,
щоб одержати нейтральні
-гіперони?
Чому дорівнює енергія реакції? Врахуйте,
що маси спокою частинок
,
щоб одержати нейтральні
-гіперони?
Чому дорівнює енергія реакції? Врахуйте,
що маси спокою частинок
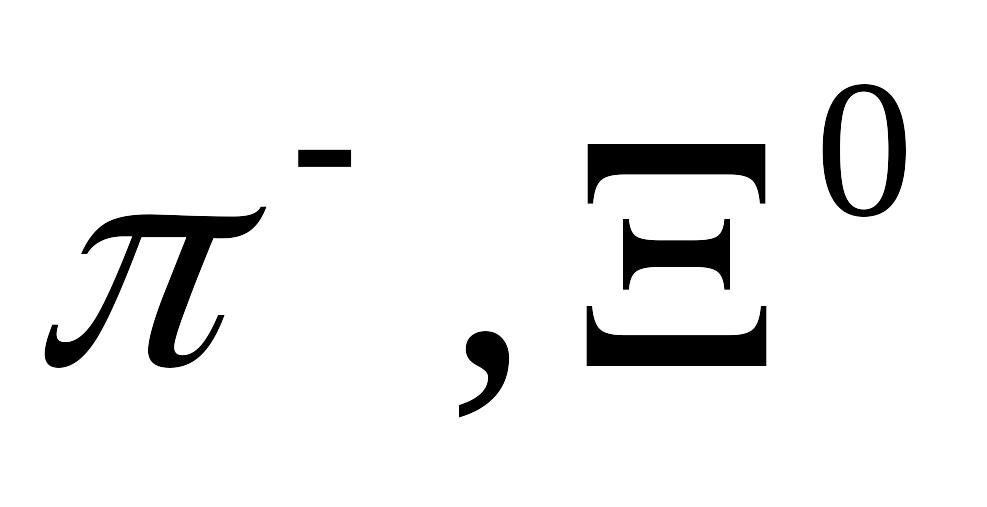 і
і
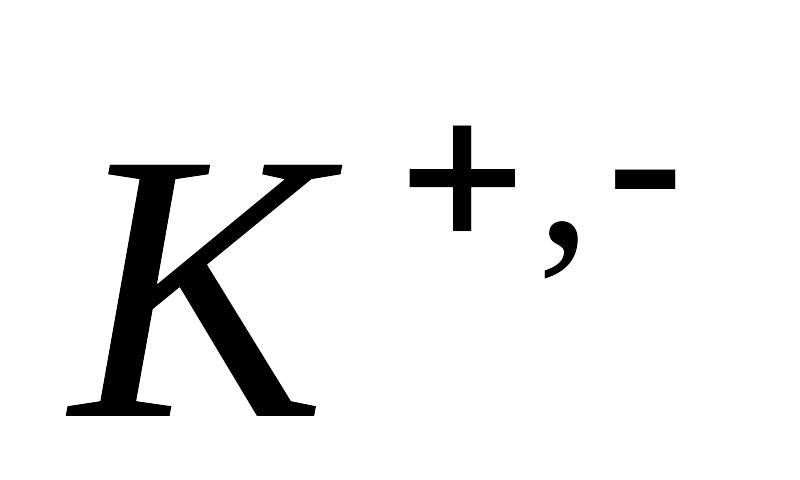 відповідно дорівнюють 0,1502952 а.о.м.,
1,41170156 а.о.м. і 0,53032743 а.о.м. [
відповідно дорівнюють 0,1502952 а.о.м.,
1,41170156 а.о.м. і 0,53032743 а.о.м. [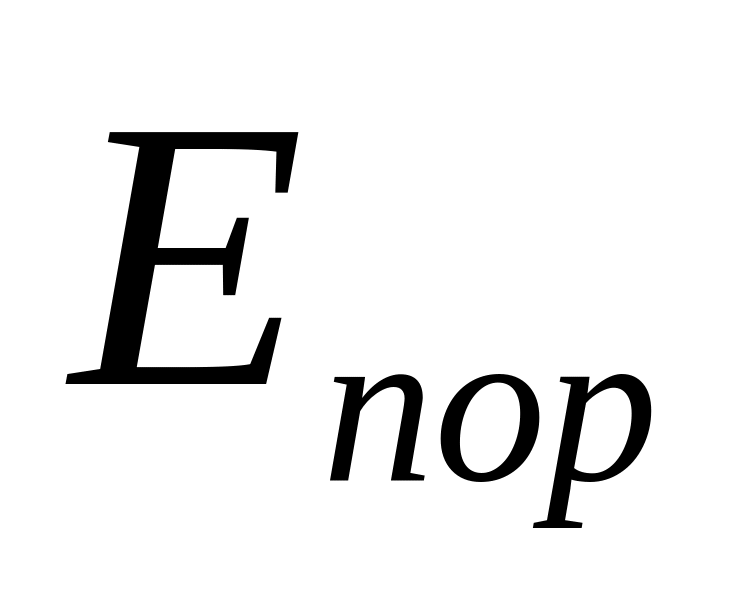 =2,21
ГеВ; Q=
=1,225 ГеВ].
=2,21
ГеВ; Q=
=1,225 ГеВ].Яку енергію повинен мати -фотон, щоб при його взаємодії з нерухомим нейтроном за схемою
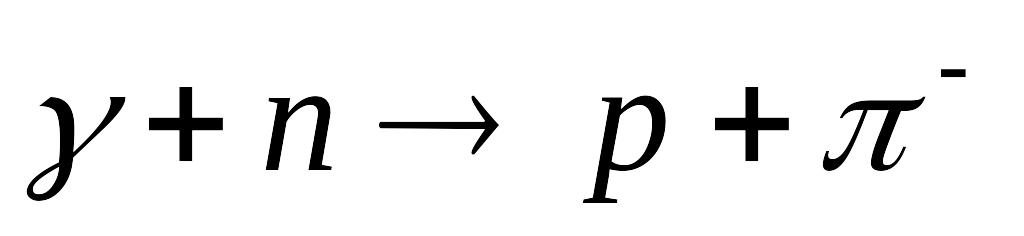 ,
народилися протон і
-мезон
з сумарною кінетичною енергією 100 МеВ?
Яку довжину хвилі має
-фотон?
Врахуйте, що маса спокою
-мезона
дорівнює 0,1502952 а.о.м.
[
=
238,6 МеВ;
=
5,21 фм].
,
народилися протон і
-мезон
з сумарною кінетичною енергією 100 МеВ?
Яку довжину хвилі має
-фотон?
Врахуйте, що маса спокою
-мезона
дорівнює 0,1502952 а.о.м.
[
=
238,6 МеВ;
=
5,21 фм].
Протон, пройшовши у лінійному прискорювачі різницю потенціалів та набув кінетичної енергії 5 МеВ. Яку швидкість має протон на виході з лінійного прискорювача? [
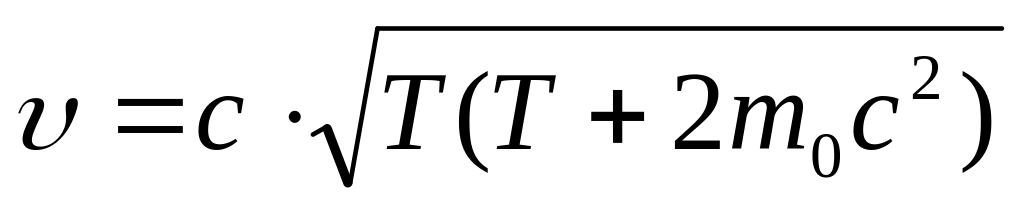 /(Т+
/(Т+ )=
=
)=
= м/с].
м/с].Високоенергетичний протон, зіткнувшись з нерухомою водневою мішенню у реакції за схемою
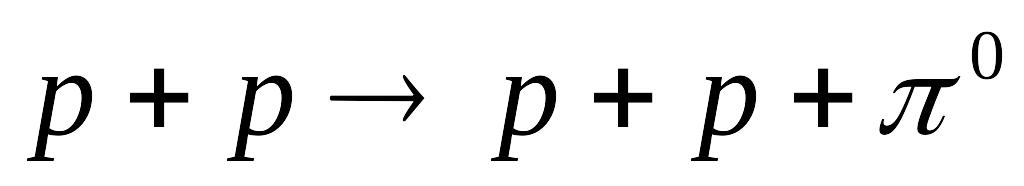 ,
породжує нейтральний
-мезон.
Яку найменшу кінетичну енергію повинен
мати у цьому випадку бомбардуючий
протон? Врахуйте,що маса спокою
-мезона
дорівнює 0,1449275 а.о.м. [279,7
МеВ].
,
породжує нейтральний
-мезон.
Яку найменшу кінетичну енергію повинен
мати у цьому випадку бомбардуючий
протон? Врахуйте,що маса спокою
-мезона
дорівнює 0,1449275 а.о.м. [279,7
МеВ].Визначте кінетичну енергію -мезона, в якого після розпаду за схемою
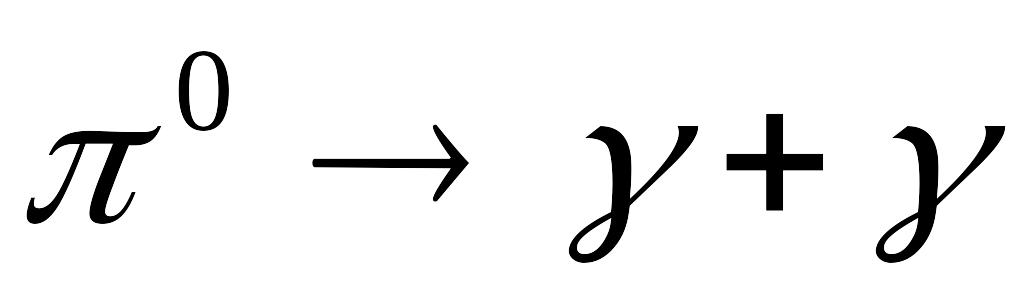 народилися два
-фотони
з однаковими енергіями, а кут між
напрямками їх руху складає
=
51,7º. Прийміть до уваги, що фотони
розлітаються симетри чно відносно
напрямку руху
-мезона,
в якого маса спокою дорівнює
0,2406∙10−27
кг. [175
МеВ].
народилися два
-фотони
з однаковими енергіями, а кут між
напрямками їх руху складає
=
51,7º. Прийміть до уваги, що фотони
розлітаються симетри чно відносно
напрямку руху
-мезона,
в якого маса спокою дорівнює
0,2406∙10−27
кг. [175
МеВ].Після народження
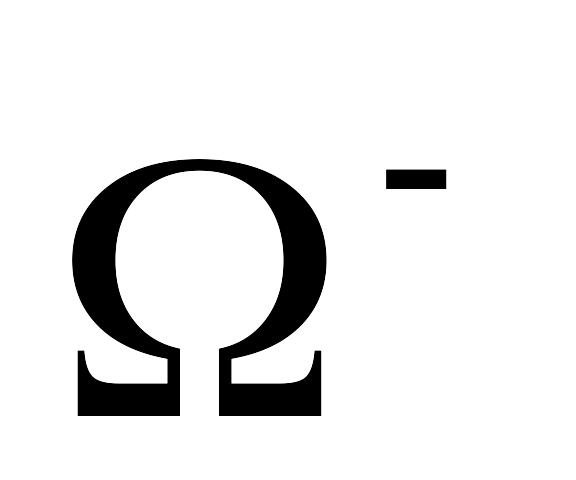 -гіперон,
володіючи кінетичною енергією 6,73 ГеВ,
пролетів у нерухомій системі відліку
до точки розпаду відстань 19,2 см.
Визначте власний час життя
-гіперона,
прйнявши, що його маса спокою дорівнює
2,972444∙10−27
кг. [
-гіперон,
володіючи кінетичною енергією 6,73 ГеВ,
пролетів у нерухомій системі відліку
до точки розпаду відстань 19,2 см.
Визначте власний час життя
-гіперона,
прйнявши, що його маса спокою дорівнює
2,972444∙10−27
кг. [
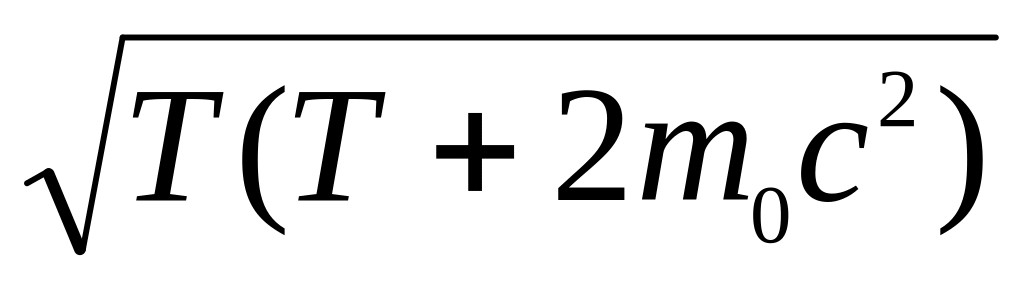 =
1,3
c].
=
1,3
c].Додатньо заряджена частинка розганяється у фазотроні з радіусом дуантів 3 м та індукцією магнітного поля 1,54 Тл до такої енергії, що її відношення до маси частинки в цей момент
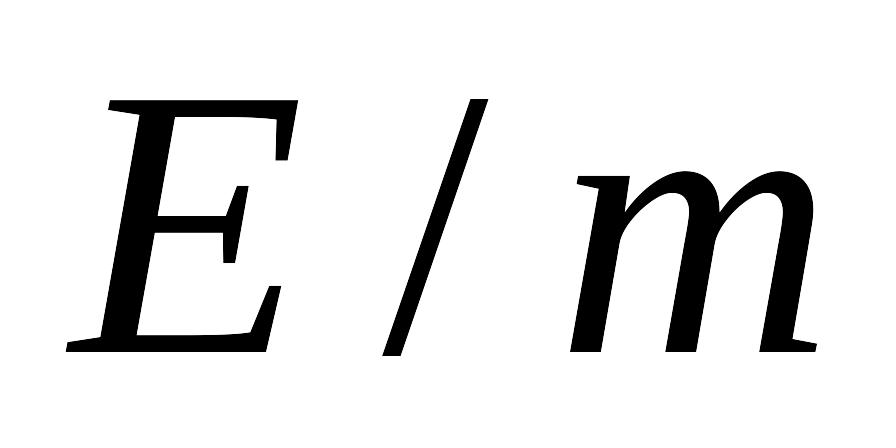 =
1,65∙1016
Дж/кг. Визначте, про яку частинку йде
мова, якщо відомо, що її маса за час
прискорення зросла на 22,5%. [q/m=
4,81∙107 Кл/кг;
це
−
-частинка].
=
1,65∙1016
Дж/кг. Визначте, про яку частинку йде
мова, якщо відомо, що її маса за час
прискорення зросла на 22,5%. [q/m=
4,81∙107 Кл/кг;
це
−
-частинка].
Д о д а т к и
Додаток 1. Фундаментальні фізичні сталі
Назва величини |
Позна−чення |
Значення величини |
|
Універсальні сталі |
|||
Швидкість світла у вакуумі |
с |
299 692 458 мс-1 |
|
Магнітна стала |
0 |
4·10-7 Гн/м = 12,566 370 614 10-7 Гн/м |
|
Електрична стала |
0 |
8,854 187 817 10-12 Фм-1 |
|
Гравітаційна стала |
G |
(6,672 59 0,000 85)10-11 м3кг-1с-2 |
|
Стала Планка |
h |
(6,626 0755 0,000 0040)10-34 Джс |
|
Стала Дірака |
|
(1,054 572 66 0,000 000 63)10-34 Джс |
|
Електромагнітні сталі |
|||
Елементарний заряд |
е |
(1,602 177 33 0, 000 000 49)10-19 Кл |
|
Магнетон Бора |
В |
(9,274 0154 0, 000 0031)10-24 ДжТл-1 |
|
Ядерний магнетон |
|
(5,050 7866 0,000 0017)10-27 ДжТл-1 |
|
Атомні сталі |
|||
Стала Рідберга |
R∞ |
10 973 731,534 0,013 м-1 |
|
Борівський радіус |
a0 |
(0,529 177 249 0,000 000 024)10-10 м |
|
Електрон |
|||
Маса cпокою електрона |
me |
(9,109 3897 0,000 0054)10-31 кг |
|
Відношення заряду електрона до його маси |
e/m |
(-1,758 819 62 0,000 000 53)1011 Клкг-1 |
|
Класичний радіус електрона |
re |
(2,817 940 92 0,000 000 38)10-15 м |
|
Магнітний момент електрона |
e |
(928,477 01 0,000 31)10-26 ДжТл-1 |
|
Протон |
|||
Маса спокою протона |
mp |
(1,672 6231 0,000 0010)10-27 кг |
|
Нейтрон |
|||
Маса спокою нейтрона |
mn |
(1,674 9286 0,000 0010)10-27 кг |
|
Додаток 2. Періоди піврозпаду деяких радіоактивних речовин
83Ві210 |
5,02 доби |
86Rn222 |
3,82 доби |
77Іг192 |
75 діб |
38Sr90 |
28 років |
20Са45 |
164 доби |
90Th232 |
1,39∙1011 років |
11Na24 |
14,9 год |
92U235 |
7,1∙108 років |
11Na22 |
2,6 роки |
92U238 |
4,5∙109 років |
84Ро210 |
138 діб |
90Th229 |
7340 років |
84Po218 |
3 хв |
88Ra219 |
14,8 діб |
7N13 |
10 хв |
88Ra226 |
1620 років |
15P32 |
14,3 доби |
82Pb211 |
36,1 хв |
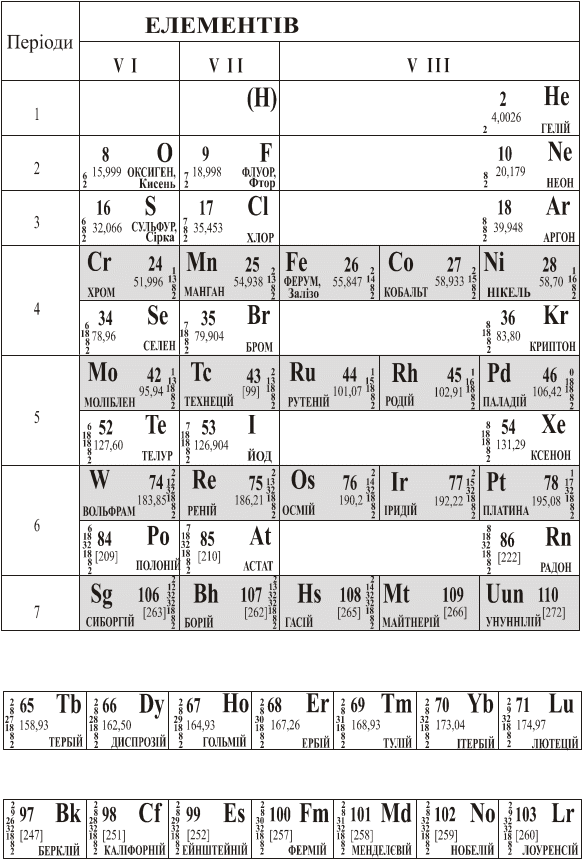
Додаток 3. Маси деяких ізотопів, а. о. м.
Ізотоп
|
Маса
|
Ізотоп
|
Маса
|
1Н1
|
1,00783
|
8O17
|
15,99491
|
1D2
|
2,01410
|
9F19
|
18,99840
|
1Т3
|
3,01605
|
10Ne20
|
19,99244
|
2Не3
|
3,01603
|
11Na23
|
22,98977
|
2Не4
|
4,00260
|
11Na24
|
23,99097
|
3Li6
|
6,01512
|
13Al27
|
26,98154
|
3Li7
|
7,01600
|
13Al28
|
27,97690
|
4Ве7
|
7,01693
|
14Si30
|
29,97377 |
4Ве8
|
8,00531
|
15P31
|
30,97376
|
4Ве9
|
9,01218
|
26Fe56 |
55,9349 |
5B10 |
10,01294 |
27Co59 |
58,9332 |
5B11 |
11,0093 |
29Ni60 |
59,9308 |
6C12 |
12,0 |
54Xe131 |
130,9051 |
7N13 |
13,00574 |
92U235 |
235,0493 |
7N14 |
14,00307 |
92U238 |
238,05353 |
Додаток 4. Грецький алфавіт
-
А, α— альфа
N, ν — ню
В, β — бета
Ξ, ξ — ксі
Г, γ— гамма
О, о — омікрон
Δ, δ — дельта
II, π — пі
Е, ε — епсилон
Р, ρ — ро
Ζ, ζ— дзета
Σ, σ— сигма
Н, η — ета
Т, τ— тау
Θ, θ — тета
Y , υ − іпсилон
І, ι— йота
Φ, φ − фі
К , κ — каппа
X , χ — хі
Λ, λ — ламбда
Ψ, ψ— псі
М, μ — мю
Ω, ω — омега
Приставки СІ для утворення кратних і дольових одиниць
|
Назва приставки |
Позначення |
Множник |
кратні |
екса |
Е |
1018 |
пета |
П |
1015 |
|
тера |
Т |
1012 |
|
гіга |
Г |
109 |
|
мега |
М |
106 |
|
кіло |
к |
103 |
|
гекто |
г |
102 |
|
дека |
да |
10 |
|
дольові |
деци |
д |
10-1 |
санти |
с |
10-2 |
|
мілі |
м |
10-3 |
|
мікро |
мк |
10-6 |
|
нано |
н |
10-9 |
|
піко |
п |
10-12 |
|
фермо |
ф |
10-15 |
|
атто |
а |
10-18 |