5.6. Квантові явища у твердих тілах Довідковий матеріал

• Внутрішня енергія одного моля хімічно простих твердих тіл за класичною теорією теплоємності:

U_m= 3RT,

де R − універсальна газова стала, Т − термодинамічна температура.

• Молярна теплоємність хімічно простих твердих тіл (закон Дюлонга й Пті):

С_M=3R.

• Молярна теплоємність хімічно складних твердих тіл (закон Неймана−Коппа):

С_M=n·3R,

де n − загальне число частинок у хімічній формулі сполуки.

• Середнє значення енергії квантового осцилятора, що припадає на один ступінь вільності у квантовій теорії Ейнштейна:

,

де − нульова енергія ( ), ω − кругова частота коливань осцилятора.

• Молярна внутрішня енергія кристала у квантовій теорії теплоємності Ейнштейна:

,

де − молярна нульова енергія за Ейнштейном, − характеристична температура Ейнштейна.

• Молярна теплоємність кристала в квантовій теорії теплоємності Ейнштейна:

.

• При низьких температурах (Т<< ):

.

• Число власних частот твердого тіла, що припадає на інтервал частот від ω до ω+dω у квантовій теорії теплоємності Дебая:

dZ=q(ω)·dω,

де q(ω) − функція розподілу частот.

• Для тримірного кристала, що містить N атомів:

dZ= ,

де ω_max− максимальна частота, що обмежує спектр коливань.

• Енергія U твердого тіла пов’язана із середньою енергією квантового осцилятора та функцією розподілу частот q(ω) співвідношенням:

• Молярна внутрішня енергія кристала за квантовою теорією теплоємності Дебая:

,

де − молярна нульова енергія кристала за Дебаєм, − характеристична температура Дебая, .

• Молярна теплоємність кристала за Дебаєм:

.

• Граничний закон Дебая: при Т<<Θ_D:

.

• Густина енергетичних станів q(E)=dz/dE за квантовою теорією:

,

де Е − енергія вільного електрона, m − його маса, V − об’єм тіла.

• Сумарна енергія всіх вільних електронів провідності в металі при T=0 K:

,

де E_f(0) − енергія Фермі для електронів у металі при Т=0 К.

• Повне число вільних електронів у металі при Т=0 К:

.

• Розподіл Фермі за енергіями для вільних електронів у металі:

а) при Т≠ 0 К,

б) при Т= 0 К, якщо Е<E_f, ,

де dn(E) − концентрація вільних електронів, енергія яких міститься в інтервалі значень від Е до E+dE; m і E − маса й енергія електрона; E_f − рівень (або енергія) Фермі.

• Розподіл Фермі за імпульсами для вільних електронів у металі:

а) при Т≠ 0 К, ;

б) при Т= 0 К, .

• Рівень Фермі в металі при Т= 0 К:

,

де n − концентрація вільних електронів.

• Температура Т_кр виродження електронів:

.

• Середня енергія, яка припадає на один електрон при Т=0 К:

.

Задачі

5.6.1. Класична теорія теплоємності

22. Використовуючи класичну теорію теплоємності, обчислити питому теплоємність цинку й кадмію. [383,5 Дж/кг∙К; 222,6  Дж/кг∙К].

23. Густина кристала кухонної солі NaCl дорівнює 2200 кг/м³. Користуючись класичною теорією теплоємності, обчисліть теплоємність кристала NaCl об’ємом 0,5 м³. [0,977 МДж/К].

24. Обчислити питомі теплоємності кристалів KBr i CaF₂, користуючись класичною теорією теплоємності.[ 419 Дж/кг∙К; 958,8 Дж/кг∙К].

25. Маса кристала цинку дорівнює 10 г. Користуючись класичною теорією теплоємності, обчисліть зміну внутрішньої енергії кристала цинку при нагріванні його від 20 до 220 ^оС. [762,4 Дж].

26. Система, що складається з N=10²⁵ класичних тривимірових незалежних гармонічних осциляторів, перебуває при температурі 250 К. Враховуючи середнє значення енергії класичного лінійного гармонічного осцилятора при тепловій рівновазі, визначити внутрішню енергію і теплоємність системи. [103,5 кДж; 414 Дж/К].

27. Користуючись класичною теорією теплоємності, визначте зміну внутрішньої енергії зразка корунду ( ) масою 20 г при нагріванні його від 24ºС до 224ºС. [ Дж].

28. Яку теплоємність має кубик із карбіду ( ) об’ємом 125 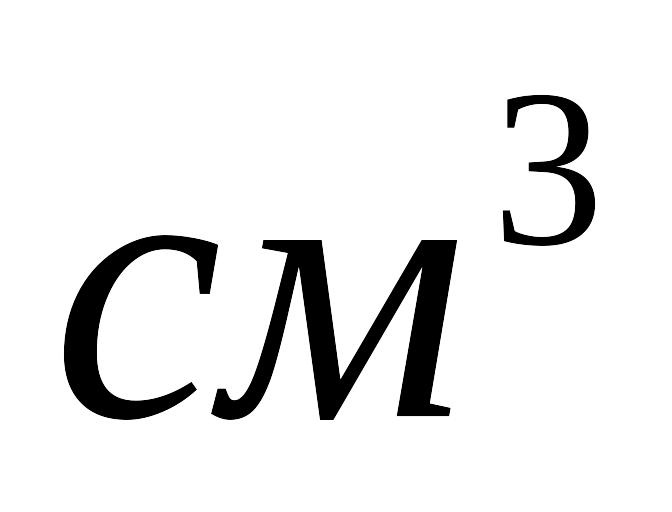, якщо його густина дорівнює 2350 кг/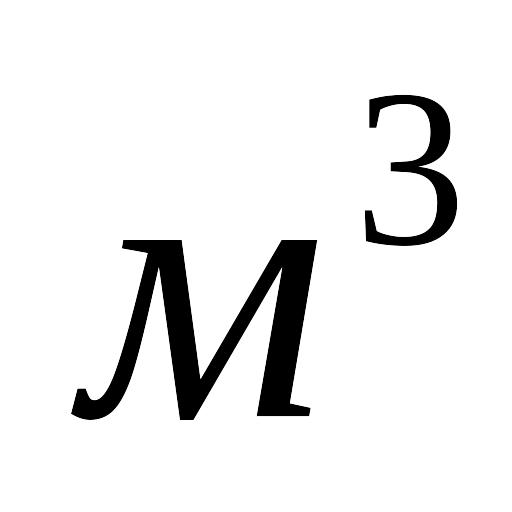 ? В розрахунках використайте класичну теорію теплоємності. [С= 356 Дж/К].

29. Обчисліть густину кристалу сульфату ( ) об’ємом 1000 , якщо його теплоємність дорівнює 3357 Дж/К. В розрахунках використайте класичну теорію теплоємності. [ кг/м³].

30. При повільному збільшенні температури кристалу нітрату ( 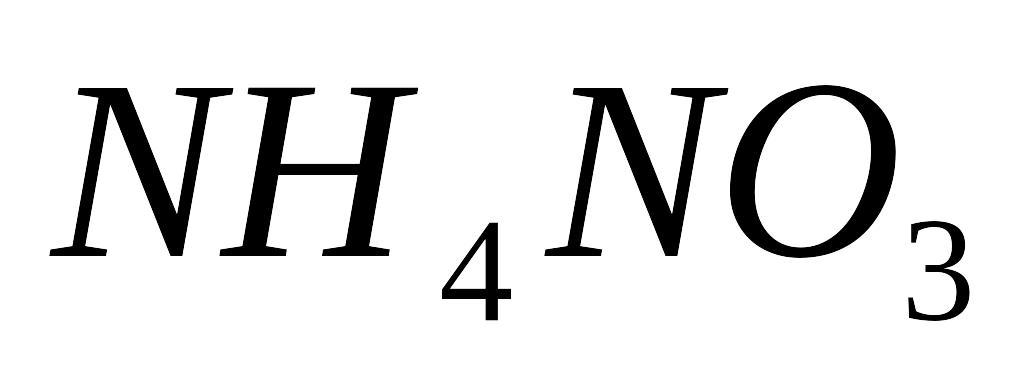) від 10ºС до 100ºС, його внутрішня енергія збільшилась на 126,21 Дж. Користуючись класичною теорією теплоємності, визначте масу досліджуваного кристалу.[ 50 г].

31. Визначте внутрішню енергію у куска цинку при 27ºС прийнявши, що в ньому міститься N= 3,683 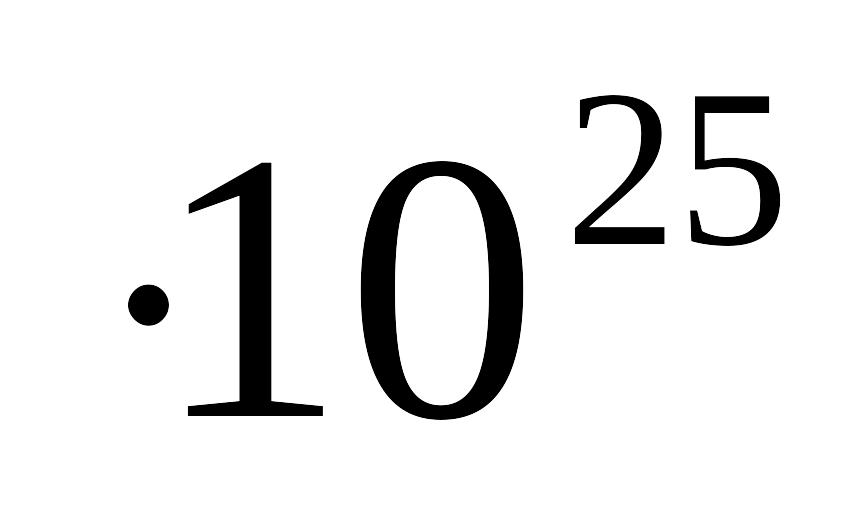класичних 3-вимірних незалежних гармонічних осциляторів. Яка питома теплоємність цієї системи? В розрахунках використайте середнє значення енергії класичного лінійного осцилятора при тепловій рівновазі. [U= 457,43 кДж; с= 381 Дж/(кг·К)].