
Свойства выпуклых функций
1. Функция f выпукла на выпуклом множестве Х в том и только в том случае, если справедливо неравенство Иенсена:
f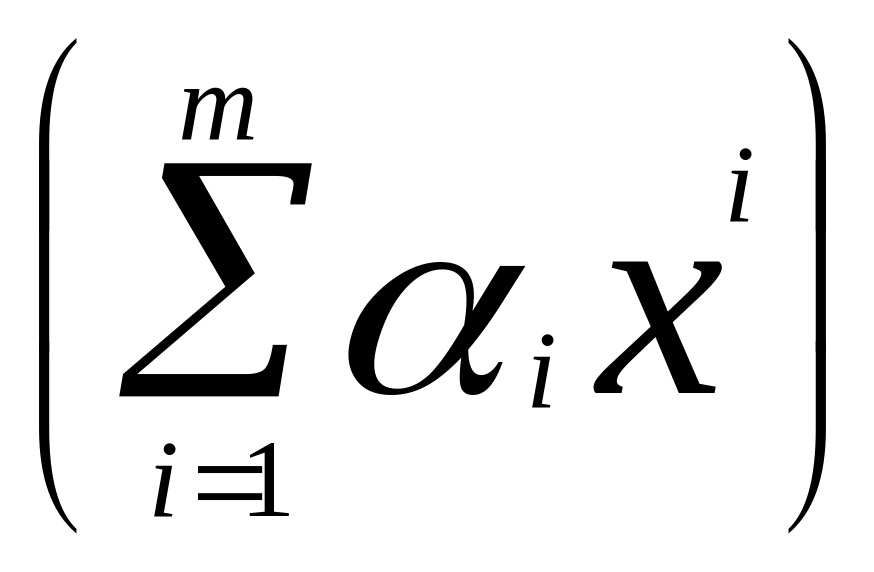
![]()
для любого m, любых xi
X,
i =
и любых αi
0,
i =
,
![]() =
1.
=
1.
2. Пусть fi, i = - выпуклые функции на выпуклом множестве Х, тогда
а) f(x) =
![]() -
выпуклая функция если αi
0,
i =
.
-
выпуклая функция если αi
0,
i =
.
б) f(x) =![]() fi(x)
– выпуклая функция, где I
– произвольное множество индексов.
fi(x)
– выпуклая функция, где I
– произвольное множество индексов.
3. Пусть g – выпуклая
функция на выпуклом множестве Х
Rn
,
![]() :
R
R
– неубывающая выпуклая функция.
Тогда функция f(x)
=
(g(x))
выпукла на Х.
:
R
R
– неубывающая выпуклая функция.
Тогда функция f(x)
=
(g(x))
выпукла на Х.
4. Пусть
- выпуклая функция на Rm,
A – матрица размера m![]() n,
b
Rm.
Тогда функция
n,
b
Rm.
Тогда функция
f(x) = (Ax + b) выпукла на Rn.
5. Пусть f – выпуклая функция на Rn. Тогда f непрерывна в любой внутренней точке множества dom f.
Замечание. Если функция f выпукла и конечна на выпуклом множестве Х, тогда f непрерывна в любой внутренней точке множества Х (т.е. функция f может иметь разрывы только на границе множества Х).
Критерии выпуклости
1. Функция f(x) выпукла на всём пространстве тогда и только тогда, когда функция g(t) = f(x + tp) одной переменной t [0,1] выпукла при любых х, р.
2. Дважды непрерывно дифференцируемая функция f , определенная на выпуклом множестве Х, выпукла на Х в том и только том случае, если
(f ”(x)y,y) 0 x X, y Rn,
т.е. если f ”(x) – матрица вторых производных функции f неотрицательно определена в любой точке х множества Х.
3. Пусть f(x) дважды непрерывно дифференцируема на Х, Х – выпуклое множество. Тогда f(x) – сильно выпуклая функция с параметром >0 на Х в том и только в том случае, если
(f ”(x)y,y) ||y||2 для y Rn и х Х.
Замечание. Выяснить, является ли эрмитова матрица А неотрицательно определённой можно, использовав один из следующих критериев.
1) Матрица А неотрицательно определена (А 0) тогда и только тогда, когда все её собственные значения неотрицательны.
2) А 0 в том и только в том случае, если все главные миноры (т.е. определители вида
![]() …ik
= det
…ik
= det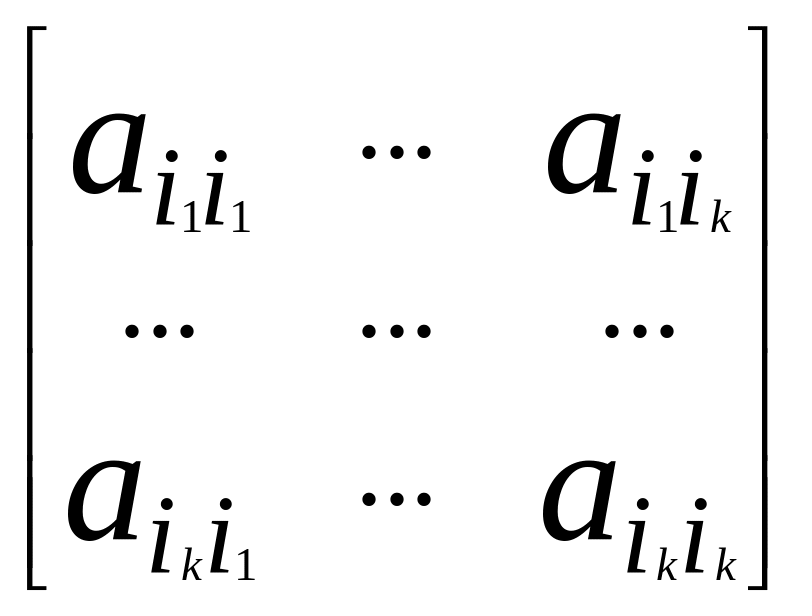 ,
,
где 1 i1<i2<…<ik n, k = ) – неотрицательны.
В теории решения экстремальных задач играют важную роль следующие теоремы.
Теорема. Пусть f(x) – выпуклая функция на выпуклом множестве Х. Тогда любая точка локального минимума f(x) на Х является точкой глобального минимума.
Теореме. Пусть f(x) – строго выпуклая функция на выпуклом множестве Х и множество её точек минимума Х* непусто. Тогда Х* состоит из единственной точки.
Теорема. Пусть f(x) – непрерывно сильно выпуклая функция с параметром >0 на Х, Х – замкнутое, выпуклое, непустое множество. Тогда решение задачи f(x) min, х Х существует и единственно.
Задачи и упражнения
1. Приведите примеры собственных и несобственных функций. Является ли
f(x)
=![]()
собственной функцией? А функция h(x) = max{f(x),0}, x R?
2. Пусть f(x) – выпуклая функция, показать, что dom f – выпуклое множество.
3. Показать, что f+(x) = max{f(x),0}, x R – является выпуклой функцией, если f(x) – выпукла на R.
4. Используя определение выпуклости, показать выпуклость следующих функций:
а) f(x) = |x|;
б) f(x) =
![]()
в) f(x) =
![]()
5. Пусть f(x) – выпуклая функция на выпуклом множестве Х. Показать, что множество
Ма(f)![]() X
= {x
X:
f(x)
a}
выпукло для любого a
Rn.
Привести пример невыпуклой функции, у
которой любое множество уровня является
выпуклым множеством.
X
= {x
X:
f(x)
a}
выпукло для любого a
Rn.
Привести пример невыпуклой функции, у
которой любое множество уровня является
выпуклым множеством.
6. Пусть gi(x), i = - выпуклые функции. Показать, что X = {x Rn : gi(x) 0, i = } – выпуклое множество.
7. Пусть f(x) – выпуклая функция. Являются ли |f(x)| выпуклой функцией?
8. Пусть f(x) – выпуклая функция и f(x) 0. Показать, что g(x) = [f(X)]2 – выпуклая функция.
9. Доказать, что ||x|| и
||x||2, x
Rn,
где ||x|| =
![]() ,
являются выпуклыми функциями. Является
ли ||x||2, x
Rn
сильно выпуклой функцией?
,
являются выпуклыми функциями. Является
ли ||x||2, x
Rn
сильно выпуклой функцией?
10. Используя определение, показать, что f(x) = ax2 + bx + c, x R выпукла при любом а>0. Является ли эта функция сильно выпуклой?
11. Пусть f(x) = ||Ax – b||2, где А – заданная матрица n m, b Rn. Доказать, что f(x) выпукла на Rm, а если АТА – невырождена, то а) f(x) выпукла на Rm; б) f(x) сильно выпукла на Rm. Найти f ’(x), f ’’(x).
12. Используя определение выпуклости
функций, показать, что J(x(.))
=
 -
выпуклая функция, если x(.)
: [t0, t1]
R,
x(.)
C([t0,
t1]).
-
выпуклая функция, если x(.)
: [t0, t1]
R,
x(.)
C([t0,
t1]).
13. Используя критерий выпуклости дифференцируемых функций, показать, что f(x) – выпуклая функция:
a) f(x) = -lnx, x>0;
б) f(x) = eαx, α – произвольное число;
в) f(x) = x-1, x>0;
г) f(x) = xP, x 0, p 1;
д) f(x) =
![]() ,
x
{x
R2|x2>0};
,
x
{x
R2|x2>0};
е) f(x) = 2x12 + x1x2 + x22, x R2.
14. Показать , что если f(x)
– выпуклая функция и f(x)<0
для любого х, то g(x)
=
![]() также является выпуклой.
также является выпуклой.
15.* Является ли функция f(x)
= ln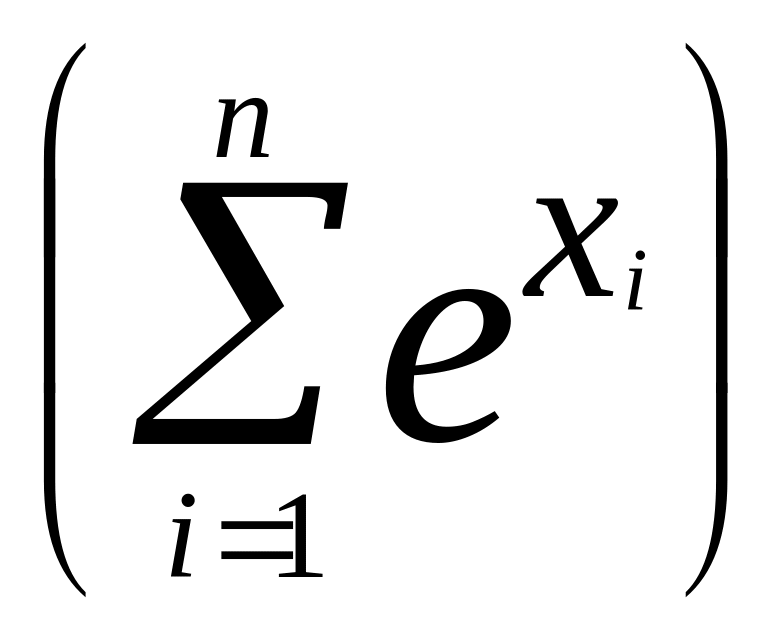 ,
x
Rn
выпуклой?
,
x
Rn
выпуклой?
16. Верно ли, что если f(x) – выпуклая функция на [a,b] dom f, a, b R, то она непрерывна на [a, b]? Верно ли, что выпуклая на (a, b) dom f, a, b R функция является непрерывной?
17. Используя неравенство Иесена и выпуклость функции g(x), доказать, что
a)
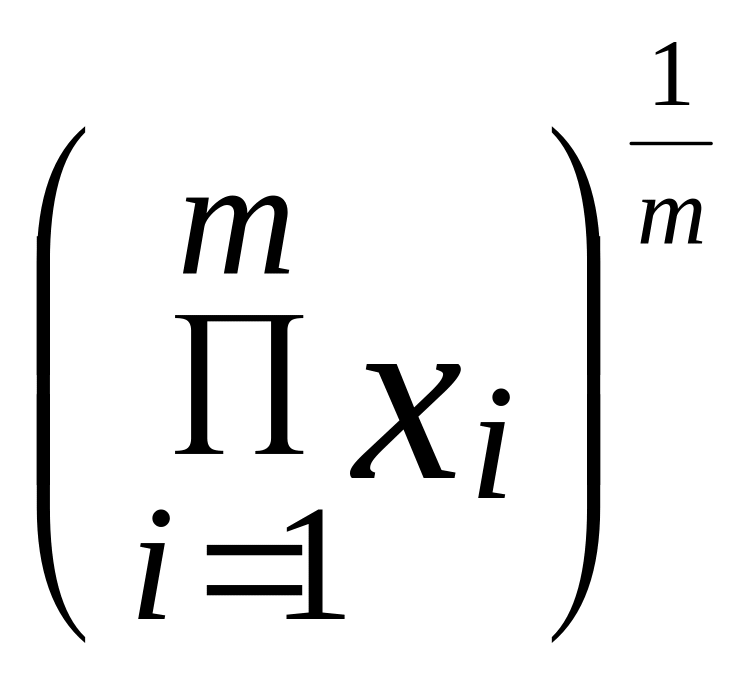
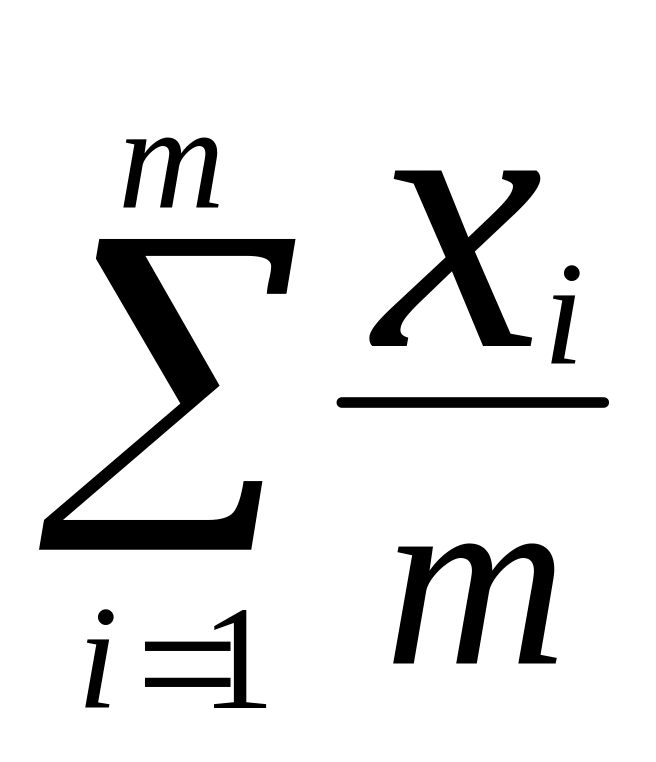 для xi
0,
i =
(использовать выпуклость g(x)
= -lnx, x>0);
для xi
0,
i =
(использовать выпуклость g(x)
= -lnx, x>0);
б)
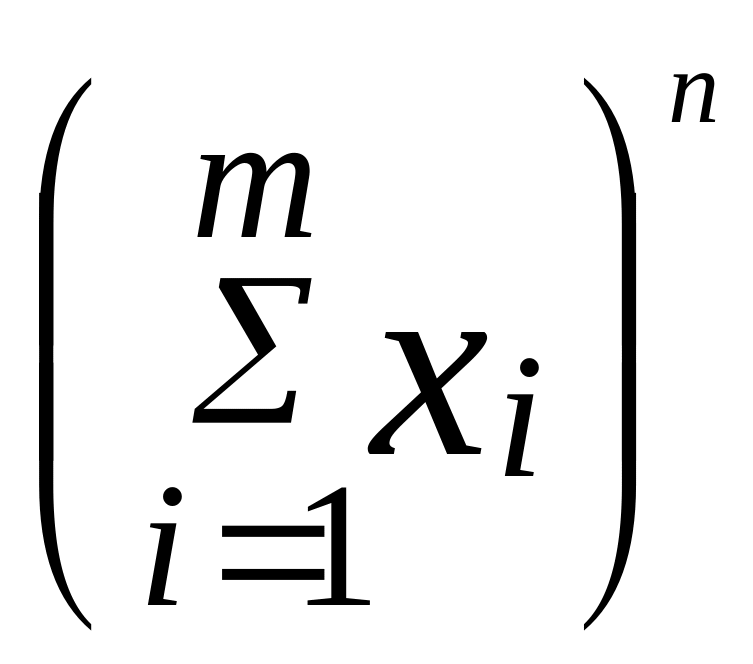 mn-1
mn-1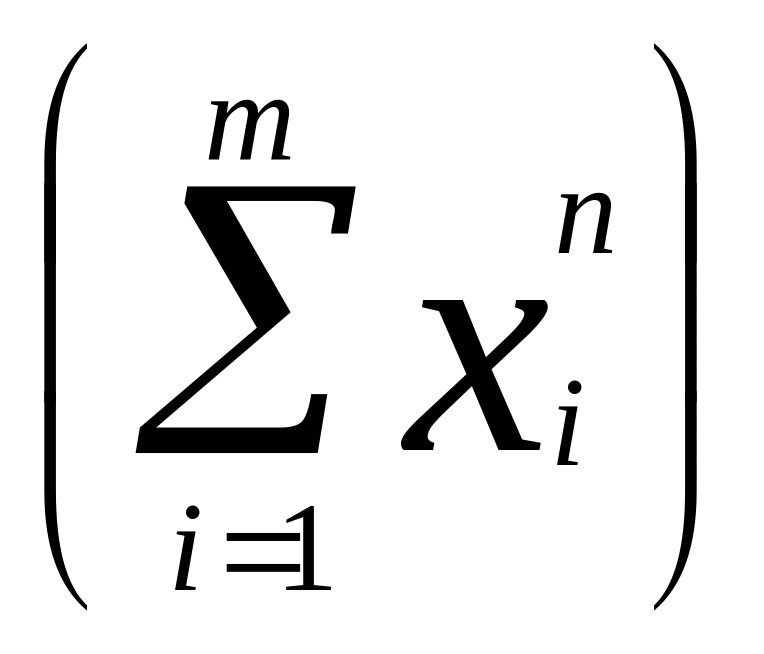 ,
xi>0,
i =
.
(использовать выпуклость g(x)
= xP,
P
1,
x
0);
,
xi>0,
i =
.
(использовать выпуклость g(x)
= xP,
P
1,
x
0);
в)
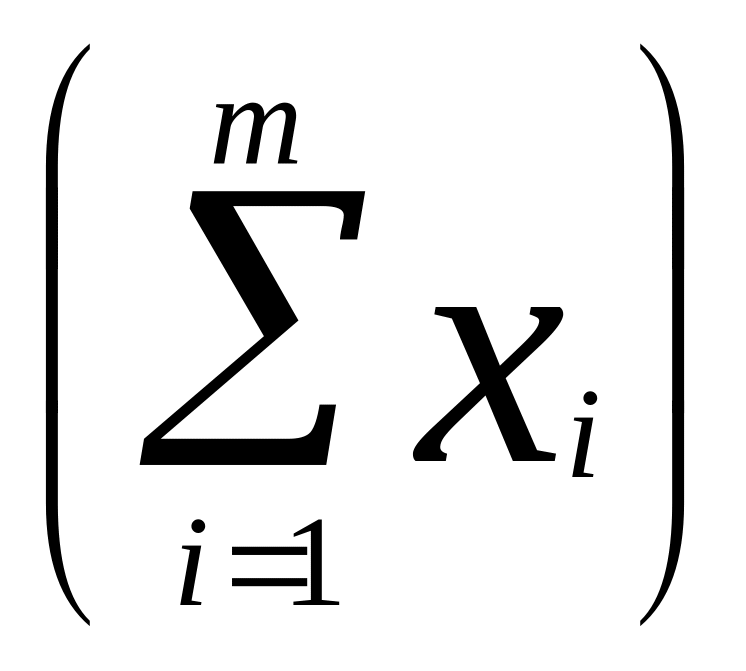
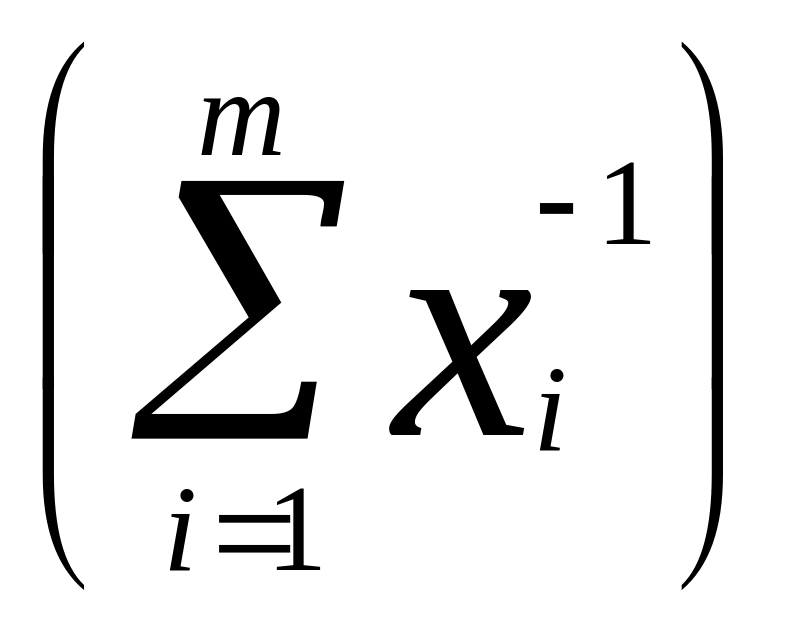 m2,
xi
> 0, i =
.
(использовать выпуклость g(x)
= x-1, x>0).
m2,
xi
> 0, i =
.
(использовать выпуклость g(x)
= x-1, x>0).
18.* Пусть
(x)
непрерывна и
(x)
0,
x
R.
Доказать, что функция f(x)
=![]() выпукла при условии, что интеграл
сходится.
выпукла при условии, что интеграл
сходится.
19.* Привести пример двух выпуклых функций, произведение которых невыпукло. При каких условиях произведение двух выпуклых функций выпукло? Достаточно ли для этого положительности сомножителей?
20.* Доказать, что функция f(x) выпукла на выпуклом множестве Х тогда и только тогда, когда функция g(x) = f(x + t(p –x)) одной переменной t[0, 1] выпукла при любых x, p X, x dom f.
21. Проверить, является ли функция f выпуклой (вогнутой) на заданном множестве Х, или указать такие точки из Х, в окрестности которых f не является ни выпуклой, ни вогнутой.
а) f(x) = x16 + x22 + x32 + x42 + 10x1 + 5x2 – 3x4 – 20, X= R4 ;
б) f(x) = 6x12 + x23 + 6x32 + 12x1 – 8x2 + 7, X = {x R3 : x 0}.
22. Выяснить, при каких значения α является выпуклыми следующие полиномы:
а) f(x) = αx12x22 + (x12 + x22);
б) f(x) = αx12x22 + (x1 + x2)4.
23. Пусть f(x) определена и выпукла на выпуклом замкнутом множестве Х. Можно ли утверждать, что
а) f(x) ограничена снизу на Х.
б) f(x) достигает своей нижней грани на множестве Х?
24. Доказать, что функция f(x)
=
![]() на [a, b]
является выпуклой функцией, где
на [a, b]
является выпуклой функцией, где
![]() C([a,
b]) и
(t)
– неубывающая функция.
C([a,
b]) и
(t)
– неубывающая функция.
