Сведения из теории

Предположим, что по экранированному контору протекает не постоянный, а переменный ток. Переменное магнитное поле контура, пронизывая экран, индуктирует в нем переменную ЭДС, вследствие чего по экрану протекает переменный ток. Экран ведет себя как коротко замкнутый виток, помещенный в переменное магнитное поле. Магнитное поле вихревых токов, протекающих по экрану, во внешнем пространстве накладывается на поле экранируемого контура со сдвигом фаз, близким к 180⁰ и ослабляет его. Чем меньше сопротивление стенок экрана и чем больше их толщина, тем меньше разница между напряженностью поля вихревых токов, протекающих по экрану и напряженностью поля экранируемого контура вне экрана.

С повышением частоты возникает явление неравномерного распределения вихревых токов в сечении материала экрана, т.е. наблюдается поверхностный эффект, который сопровождается сосредоточением этих токов на поверхности экрана. Чем выше частота, тем меньше глубина проникновения и тем выше эффективность экранирования.

Следовательно, экранирование магнитных полей складывается из двух процессов: из компенсации поля экранируемого контура полем вихревых токов, как в коротко замкнутом витке, и из ослабления поля при проникновении его через толщу стенок экрана.

Экранирование с использованием вихревых токов обеспечивает одновременное ослабление как магнитных, так и электрических полей. Это дает основание называть этот способ электромагнитным экранированием.

С точки зрения волновых представлений эффект экранирования представляется из-за многократного отражения электромагнитных волн от поверхности экрана и затухания энергии волн в его металлической толще.

Электромагнитные экраны - это устройства, предназначенные для ослабления полей в областях, не содержащих источников, и являющиеся эффективным средством подавления как внутренних, так и внешних по отношении к данной электромагнитной цепи полей, несущих информацию. Эти поля, в общем случае, различаются по типу источника помех (электрический, магнитный), амплитудно-временному признаку (вид сигнала, его спектр). В основном экраны являются линейными устройствами. Для выяснения специфики экранирования сложной амплитудно-временной структуры сигнала применим принцип суперпозиции. Эффективность экранирования зависит от ряда факторов: структуры электромагнитного поля, диапазона частот, формы экрана, размеров материала его конструкции. На эффективность экранирования существенное влияние оказывают отверстия щели в экране их форма, размеры и ориентация относительно векторов электромагнитного поля.

Особенности экранирования электро магнитных полей.

На низких частотах параметры экранов для электрических и магнитных полей сильно отличаются друг от друга, с повышением частоты сигнала помехи эти различия уменьшаются. К низким частотам относятся те случаи, когда расстояние от источника помехи до экрана R << λ , где λ длина волны сигнала помехи, R – эквивалентный радиус экрана. Указанная область соответствует ближней зоне источников поля, в которой для электрических источников (например, диполей, вибраторов) преобладает электрическое поле, а для магнитных источников (рамка с током) преобладает магнитное поле. В расчетах экрана для электрического поля нужно учитывать особенности экранирования электрического поля, а во втором магнитного.

На высоких частотах, когда R > λ, поле источников становится электромагнитным и соотношение между электрическим и магнитным полем не зависит от вида источника. В этом случае ведут расчет экранов для высоких частот. На рис. 1а приведены зависимости экранного ослабления стального и медного экранов для магнитных и электрических источников от частоты.

С точки зрения физических процессов предельные случаи электромагнитного экранирования на низких частотах - это электростатические и магнитостатические поля. Известно, что электростатическое поле полностью экранируется тонкостенным экраном Ээ ~ из любого металла с проводимостью δ > 0. Магнитостатическое поле совсем не экранируется экраном из немагнитных материалов (рис.1). Отсюда, для экранирования магнитного поля экраны изготавливают из материала с большим значением >>1 . Если увеличивать частоту электромагнитных колебаний, то с ростом частоты различие между этими двумя процессами начинает стираться. Принято считать, что эффективность экранирования с понижением частота падает, т. к. растет глубина проникновения поля в стенку экрана пропорционально увеличению толщины скин слоя Δ° (толщина скин слоя - это такая глубина проникновения поля в проводник, на которой амплитуда поля убывает в е раз).

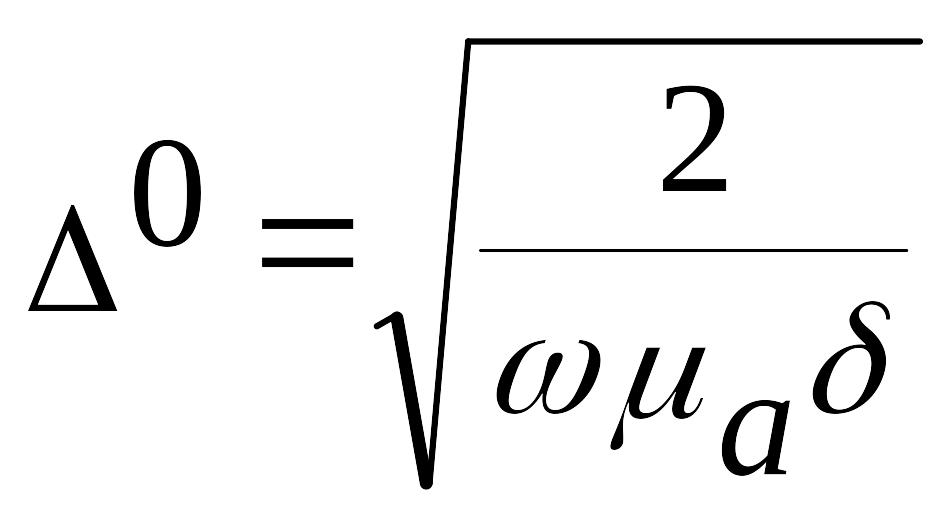
δ - удельная проводимость материала,

- круговая частота сигнала, ;

Но, с другой стороны, на самых низких частотах и особенно на нулевой частоте эффект экранирования электрического поля резко возрастает, а магнитного падает. На высоких частотах, когда толщина экрана d >> Δ°, эффективность экранирования электрических и магнитных полей сравнивается.

Физику экранирования можно объяснить по-разному:

1. Под воздействием поля помехи на экране наводятся электрические поверхностные заряды, а также токи и магнитное поле. Они создают вторичное поле, которое в результате сложения с первичным полем ослабляют его в защищенной области.

2. С другой стороны, действие экрана можно рассматривать как результат многократного отражения электромагнитной волны от его поверхности, из-за различия волновых сопротивлений окружающей среды и материала экрана, и затухания высокочастотной энергии в стенках экрана. Эффект экранирования по электрическому и магнитному полям, в этом случае, можно характеризовать как:

где - характеризует ослабление электрического и магнитного поля за счет потерь энергии в стенке экрана.

и - потери электрического и магнитного поля из-за отражений от поверхности экрана.

Качественное сопоставление этих величин для немагнитных материалов иллюстрируется на графиках (рис. 2). Анализ этих кривых показывает, что на более низких частотах эффективность экранирования в основной определяется эффектом отражения соля от поверхности экрана, а на высоких частотах главным образом эффектом поглощения.

В конструкциях экранов часто приходится предусматривать отверстия, цели. Наличие отверстий в экране снижает эффективность экранирования, и их влияние зависит от формы, размеров отверстий, его местоположения и ориентации относительно токов проводимости на экране.

Местоположения отверстий желательно выбирать в области экрана, где поле помехи минимальное. Размеры отверстия должны быть по возможности минимальными, и оно должно быть ориентировано большей стороной перпендикулярно касательным силовым линиям магнитного поля. При этом отверстие пересекает меньшее число силовых линий плотности тока проводимостей и, следовательно, оно слабее будет возбуждаться. Влияние формы отверстия сказывается на его эффективности возбуждения. Если поле помехи линейной поляризации и ее направление известно, то отверстие желательно делать узким и ориентировать его перпендикулярно магнитному полю, а если поляризация неизвестна или вращающаяся, то отверстие желательно брать квадратным, круглым. При этом эффективность его возбуждения не зависит от направления поляризации. Если одно большое отверстие можно заменить рядом маленьких, то это значительно улучшает характеристики экранирования.

Применение объемного интегрального уравнения к расчету плоского экрана

Метод объемного интегрального уравнения используется для расчета электромагнитных экранов произвольной формы численными методами. Рассмотрим теперь простой пример получения аналитического решения. На рис. 15.1 представлен фрагмент плоского экрана из однородного немагнитного материала с комплексной диэлектрической проницаемостью _r.

Рис. 15.1. Фрагмент плоского экрана

Уравнение для рассматриваемого случая имеет вид:

, (1)

где интегрирование распространяется на весь объем плоского слоя 0< z < d (d - толщина экрана), а R в аргументе функции Грина – расстояние от точки наблюдения до точки интегрирования ( , V_э). Интегрирование удобно вести в цилиндрических координатах с началом в точке наблюдения:

=|x-x_v|²+|y-y_v|², .

Ограничимся случаем нормального падения плоской волны на поверхность экрана z=0:

. (2)

Решение ищем в виде суперпозиции двух плоских волн внутри слоя:

. (3)

Интеграл (1) с учетом введенных переменных и представления решения в форме (3) можно записать в виде:

. (4)

Внутренний интеграл вычисляется аналитически. G(R) ( ) от угловой координаты не зависит.

. (5)

Для преодоления неопределенности при подстановке верхнего предела можно применить принцип предельного поглощения. Это означает, что все соотношения рассматриваются при комплексной диэлектрической проницаемости , а в конечных формулах осуществляется конечный переход . Благодаря этому в (16.5) подстановка верхнего предела дает нуль, поскольку волновое число к_е содержит небольшую отрицательную мнимую составляющую, и результат интегрирования оказывается равным:

. (6)

Интеграл (4) зависит от поперечных координат и оператор div в (1) равен нулю и поэтому само это уравнение превращается в скалярное относительно проекций полей на ось x:

. (7)

Для нахождения неизвестных амплитуд E_it и E_is в выражение для внутреннего поля E_i(z) следует подставить (3) в (7). Область интегрирования по z_v необходимо разбить на две части: z_v<z и z_v>z.

. (8)

Последовательно получим значения отдельных интегралов:

(9)

(10)

Складывая (9) и (10) и проводя элементарные преобразования, значение (16.8) можно записать в виде:

(11)

(0<z<d)

Т.е. интегрирование восстанавливает с точностью до постоянного множителя внутреннее поле, E_i(z) и дает дополнительно две волны, распространяющиеся во внешней среде в положительном и отрицательном направлении оси z. Можно увидеть, что подстановка в (7) приводит к сокращению E_i(z) в уравнении. Оно превращается в функциональное уравнение:

(12)

В этом уравнение постоянные коэффициенты при двух линейно независимых функциях exp(-i_ez) и exp(i_ez) должны быть равны нулю. Отсюда следует следующая система двух линейных уравнений относительно неизвестных коэффициентов E_it и E_is:

( + _e)E_it - ( - _e)E_is= 2_eE_0t,

(13)

( - _e)e^-id E_{i t} – ( + _e)E_ise^id = 0,

решение которой дает следующие значения неизвестных коэффициентов E_it и E_is:

, (14)

. (15)

Интересно, что если бы решение данной задачи осуществлялось на основе обычного подхода с использованием граничных условий непрерывности касательных составляющих электрического и магнитного поля на границах раздела сред z = 0 и z = d, то пришлось бы решать систему четырех уравнений с четырьмя неизвестными. Т.е. использование интегрального уравнения приводит к сокращению размерности задачи, хотя за это приходится платить некоторой предварительной процедурой вычисления интегралов.

По вычисленному внутреннему полю, можно найти поле, рассеиваемое экраном как в области z < 0 (перед экраном). Так и z  d (за экраном). Поле за экраном складывается из поля Е₀ и поля E_es, рассеиваемого экраном:

. (16)

Поле E_es вычисляется по формуле:

(17)

Подставляя сюда выражения для коэффициентов (14) и (15) получим:

. (18)

Полное поле за экраном после подстановки (18) в (16) окончательно запишется таким образом:

. (19)

Можно показать, что с учетом магнитных свойств формула усложняется незначительно:

. (20