1.2 Set Operations
In this section we introduce operations that allow us to create new sets from old sets. We define the union A B and intersection A B of sets A and B as follows:
A B = {x :x A or x B or both};
A B = {x :x A and x B}.
We added “or both” to the definition of A u B for emphasis and clarity. In ordinary English, the word “or” has two interpretations. Sometimes it is the inclusive or and means one or the other or both. This is the interpretation when a college catalog asserts: A student's program must include 2 years of science or 2 years of mathematics. At other times, “or” is the exclusive or and means one or the other but not both. This is the interpretation when a menu offers soup or salad. In mathematics we always interpret or as the “inclusive or” unless explicitly specified to the contrary. Sets A and B are said to be disjoint if they have no elements in common, i.e., if A B = .
Given sets A and B, the relative complement A\B is the set of objects that are in A and not in B:
A\B = {x :x A and x B] = {x A :x B}.
It is the set obtained by removing from A all the elements of B that happen to be in A.
The symmetric difference A B of the sets A and B is the set
A B = {x : x A or x B but not both}.
Note the use of the “exclusive or” here. It follows from the definition that
A B = (A B)\(A B) = (A\B) (B\A).
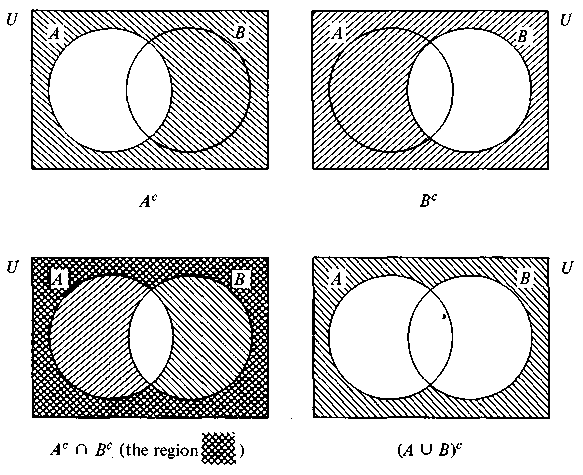
It is sometimes convenient to illustrate relations between sets with pictures called Venn diagrams, in which sets correspond to subsets of the plane. See Figure 1, where the indicated sets have been shaded in.
Figure 1
EXAMPLE 1 (a) Let A = {n N :n 11}, B = {n N :n is even and n 20}
and E = {n N: n is even}. Then we have
A B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 16, 18, 20},
A B = {0, 2, 4, 6, 8, 10},
A\B = {1, 3, 5, 7, 9, 11},
B\A = {12, 14, 16, 18, 20}.
A B = {1, 3, 5, 7, 9, 11, 12, 14, 16, 18, 20}.
We also have E B = B, B\E = { },
E\B = {n N :n is even and n 22} = {22, 24, 26, 28....},
N\E = {n N :n is odd}={l, 3, 5, 7, 9, 11,...},
A E={1, 3, 5, 7, 9, 11} {n N :n is even and n 12}
={1, 3, 5, 7, 9, 11, 12, 14, 16, 18, 20, 22,...}.
(b) Consider the intervals [0, 2] and (0,1]. Then (0,1] [0, 2] and
so
(0,1] [0,2] = [0,2] and (0,1] [0,2] = (0,1].
Moreover, we have
(0,1]\[0, 2] = { },
[0,2]\(0,1] = {0} (1,2] and [0,2]\(0,2) = {0,2}.
(c) Let = {a, b}, A = {, a, aa, aaa}, B = {, b, bb, bbb} and C = {w
*:length(w) 2}. Then we have
A B = {, a, b, aa, bb, aaa, bbb}, A B = {A},
A\B = {a, aa, aaa}, B\A = {b, bb, bbb},
A C = {, a, aa}, B\C = {bbb},
C\A = {b, ab, ba, bb}, A\I. = {, aa, aaa}. ■
It is often convenient to fix some set U, such as N, R or *, which we call the universe or universal set, and to consider only elements in U and only subsets of U. For A U the relative complement U\A is called in this setting the absolute complement or simply the complement of A and is denoted by Ac. Note that the relative complement A\B can be written in terms of the absolute complement: A\B = A B. In the Venn diagrams in Figure 2 we have drawn the universe U as a rectangle and shaded in the indicated sets.
