Лабораторная работа № 9. Метод математической индукции Вопросы к работе.
Для какого типа утверждений применяется метод математической индукции?
В выполнение каких шагов состоит метод математической индукции?
Образцы решения заданий.
1. Доказать, что
сумма первых
(
)
нечетных чисел равна квадрату их числа,
т. е.
.
Решение.
Т. к. утверждение зависит от натурального параметра , то воспользуемся для его доказательства методом математической индукции.
1) Проверим справедливость данного утверждения для .
Если
,
то
(и).
2)Предположим, что
сумма первых
(
)
нечетных чисел равна квадрату количества
этих чисел, т. е.
.
Другими словами, предположим, что наше
утверждение истинно для всех, значений
от 2 до
включительно.
3) Установим, исходя
из равенства (2), что сумма первых
нечетных чисел равна
,
т. е.1+3+5+…+(2(k+1)-1)=
.
Действительно,
1+3+5+…+(2(k+1)-1)=1+3+5+…+(2k+1)=1+3+5+…+(2k–
–1)+( 2k+1)=[1+3+5+…+(2k-1)]+
(2k+1)=
+2k+1=
;
=
(и).
На основании
принципа математической индукции делаем
вывод, что сумма первых n
нечетных чисел равна
для любого натурального
.
2. Доказать, что
для
-го
члена геометрической прогрессии
со знаменателем q
справедлива формула
(
).
Решение.
Доказательство проводим методом математической индукции по натуральному параметру n.
n=1
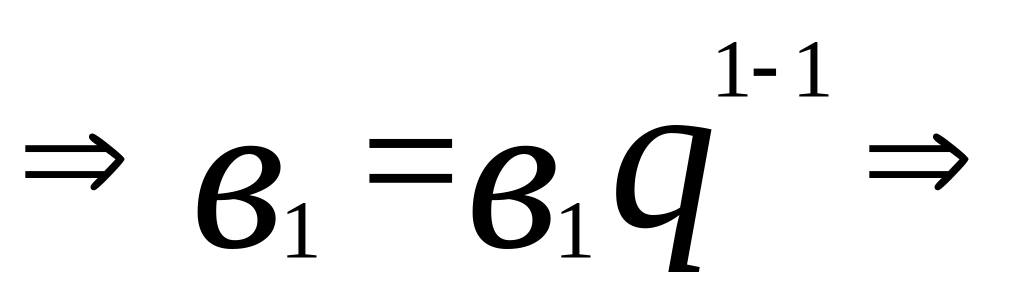
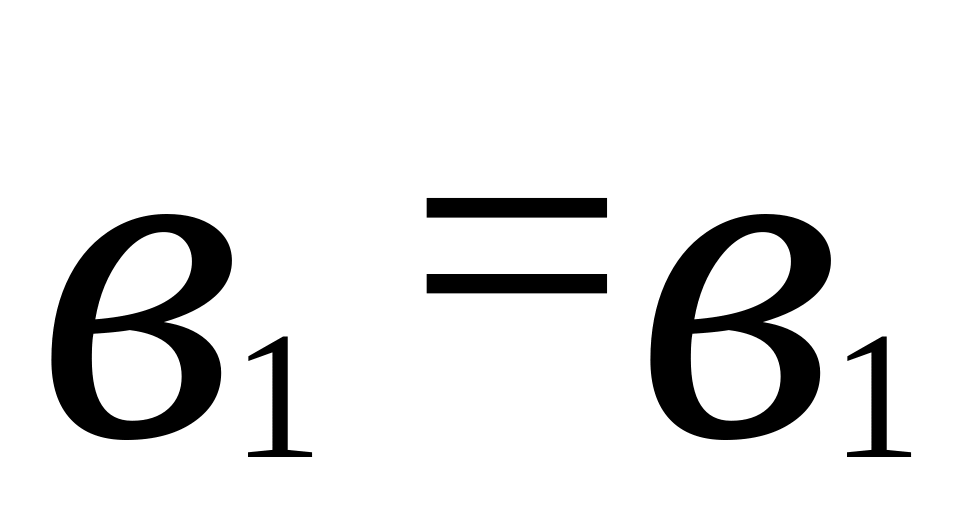(и).Предположим, что формула справедлива для всех натуральных значений n от 2 до k включительно, т. е.
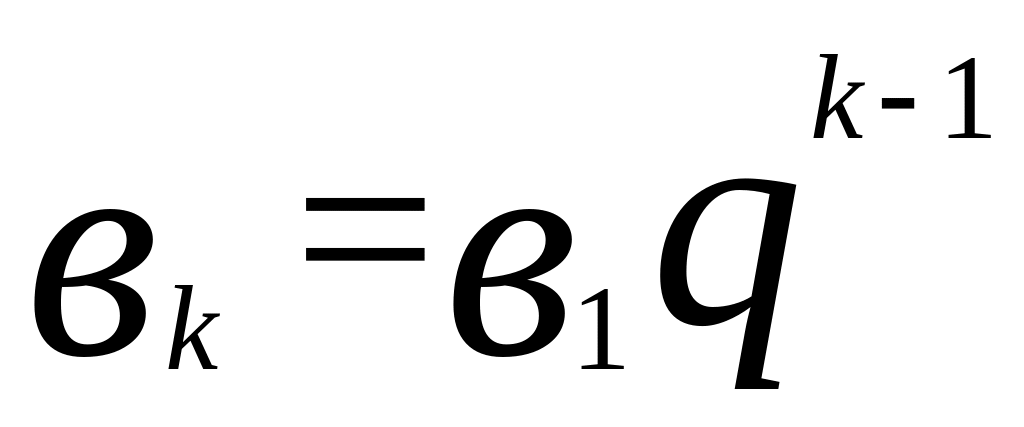
n=k+1
=
;
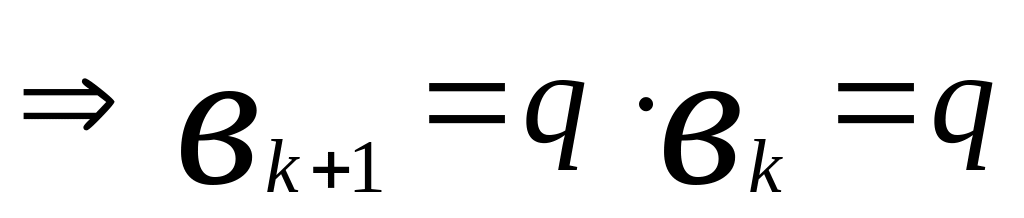
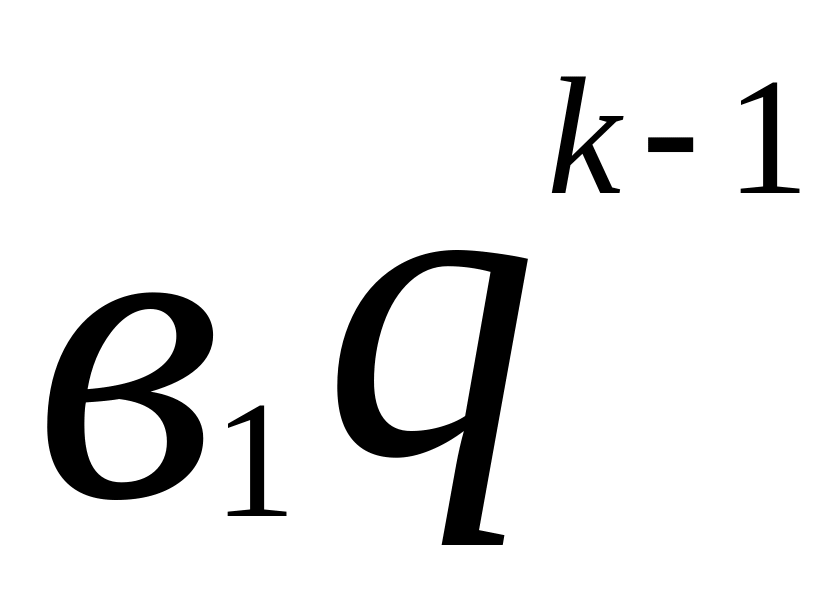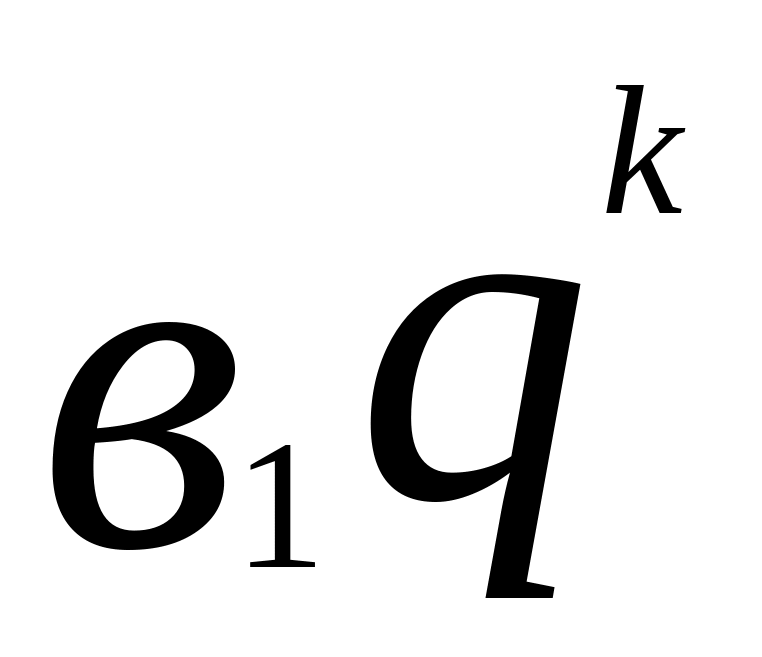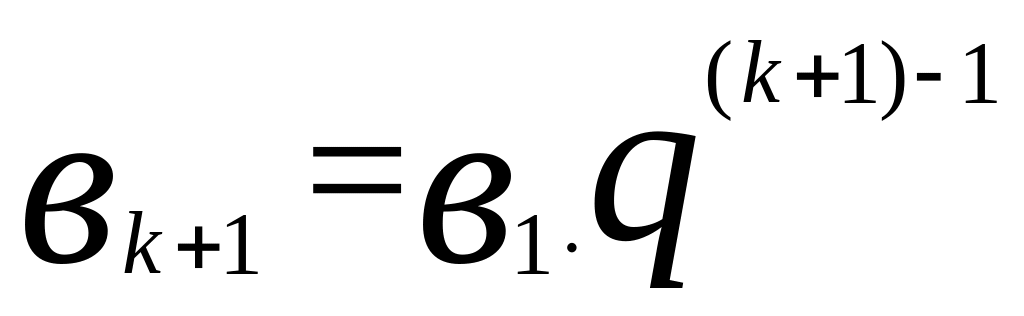(и).
Согласно принципа математической индукции можно сказать, что рассматриваемая формула верна для любого натурального n.
Доказать, что при каждом натуральном n число
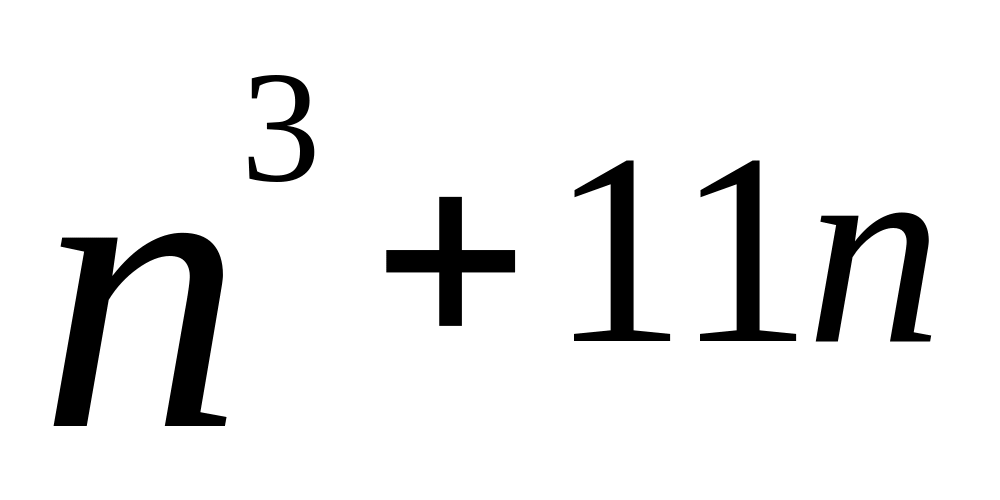делятся на 6.
Решение. Обозначим
число
=
.
Надо доказать, что
6
при любом натуральном n.
n=1
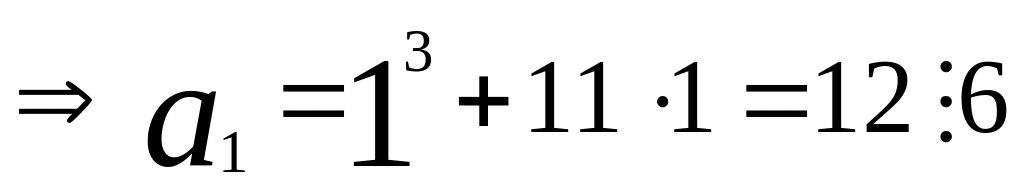(и).
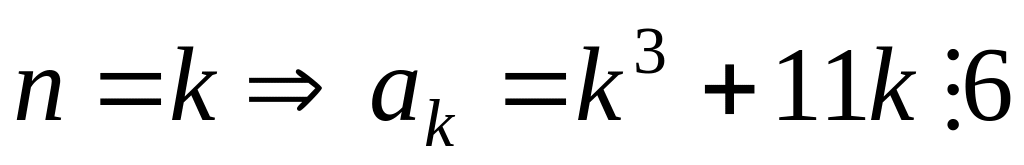(предположение)n=k+1
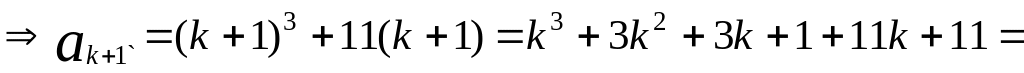
(по
предположению),
(по свойствам делимости).
Если мы сумеем доказать, что
,
то тогда можем утверждать, что
,
т. к. 3 и 2 взаимно-простые числа.
Это доказательство проведем тоже методом математической индукции:
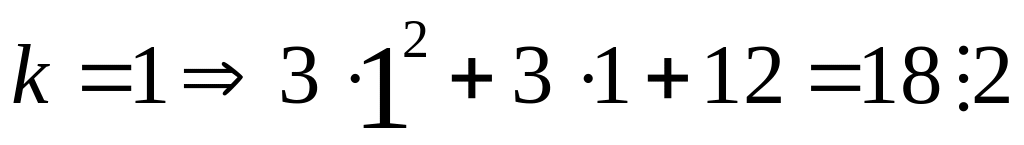
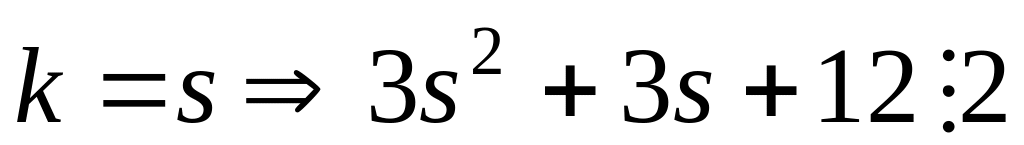(предположение)
3)
(по
предположению)
(6S+6)
(по
свойствам делимости).
Тогда
по свойству делимости.
Итак
и
2. Следовательно,
.
Согласно методу математической индукции мы можем сказать, что число делится на 6 для любого натурального значения n.
Доказать, что при каждом натуральном справедлива формула 1+2+3+….+(n-1)+n=
.
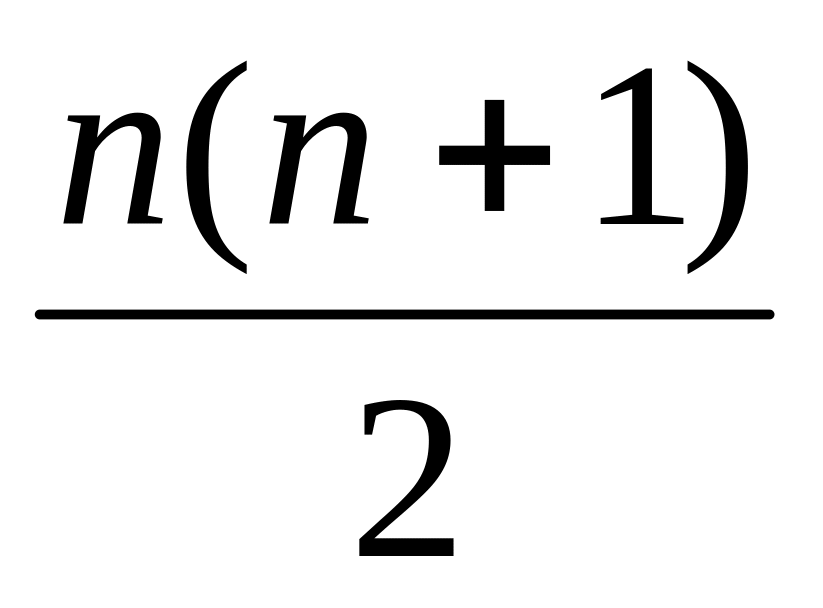Решение.
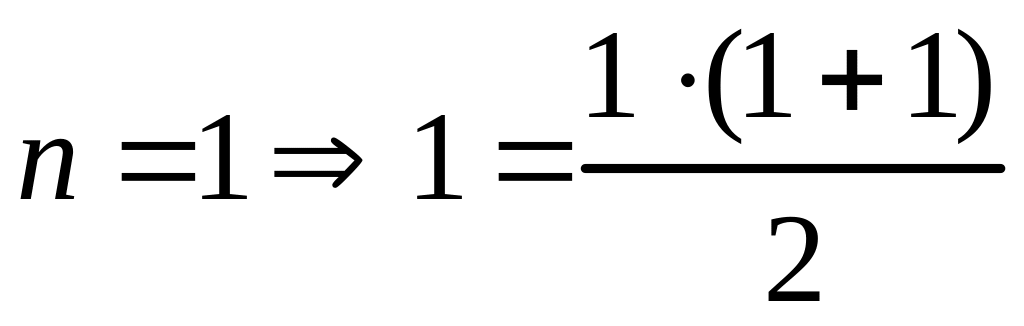; 1=1(и).
(предположение).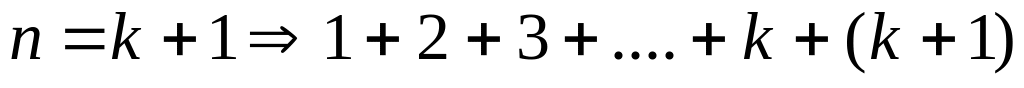
равно ли
?
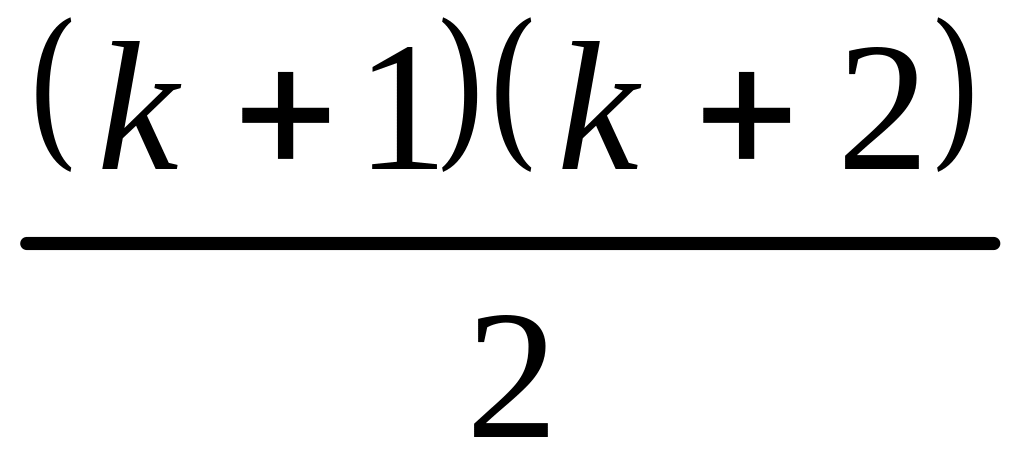Обозначим
,
Чтобы доказать,
что
,
мы можем
с помощью тождественных преобразований перевести в ;
с помощью тождественных преобразований перевести в ;
с помощью тождественных преобразований перевести в
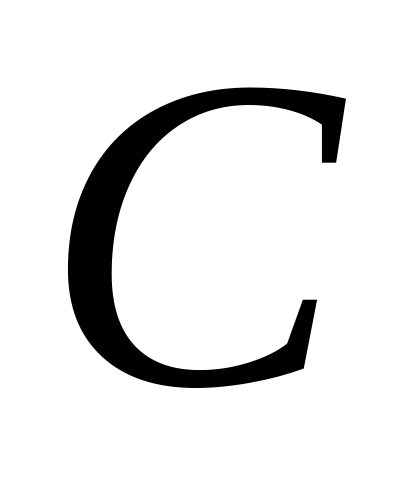;с помощью тождественных преобразований перевести в ;
Воспользуемся приемом (3)
1+2+3+…+k+(k+1)=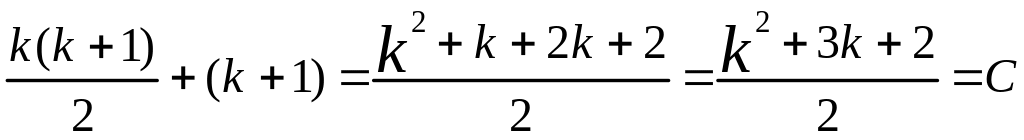
;
;
=
.
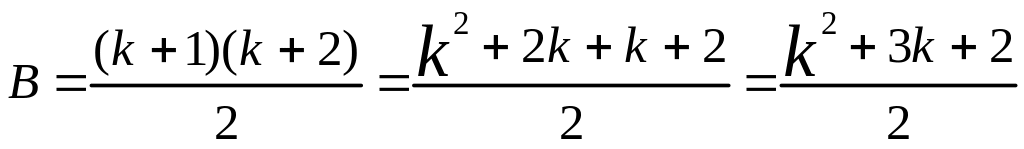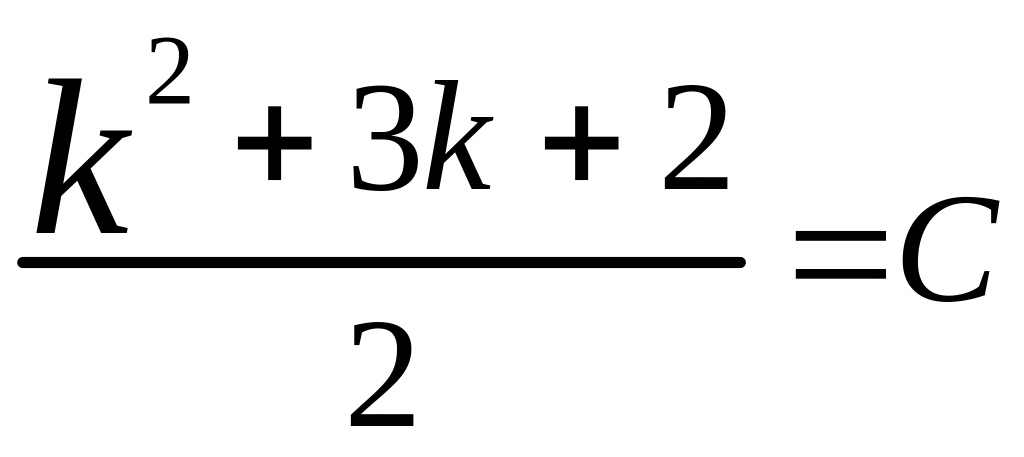Значит,
,
т. е. при
наше утверждение – истина.
Согласно принципа
математической индукции делаем вывод:
1+2+3+…+ n=
при
.
Последовательность
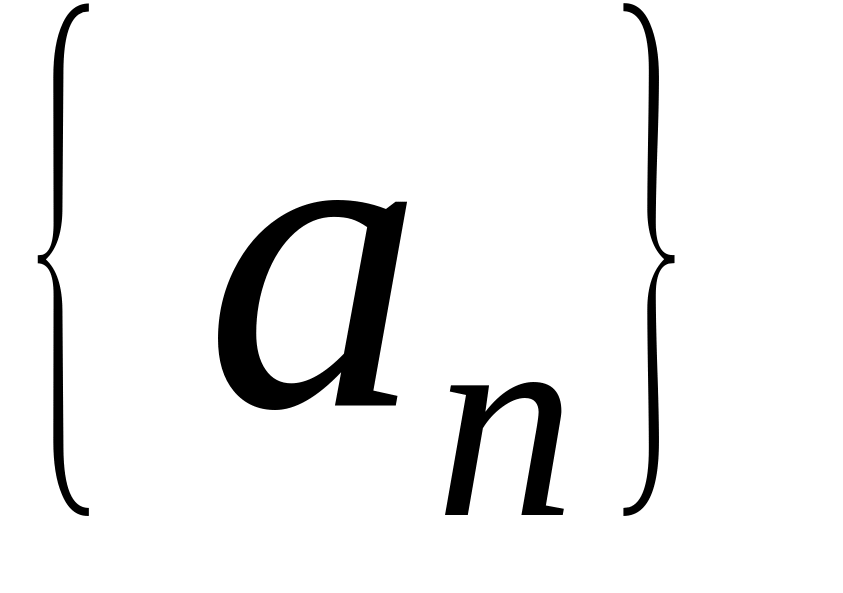задана рекуррентным соотношением:
,
,
,
.
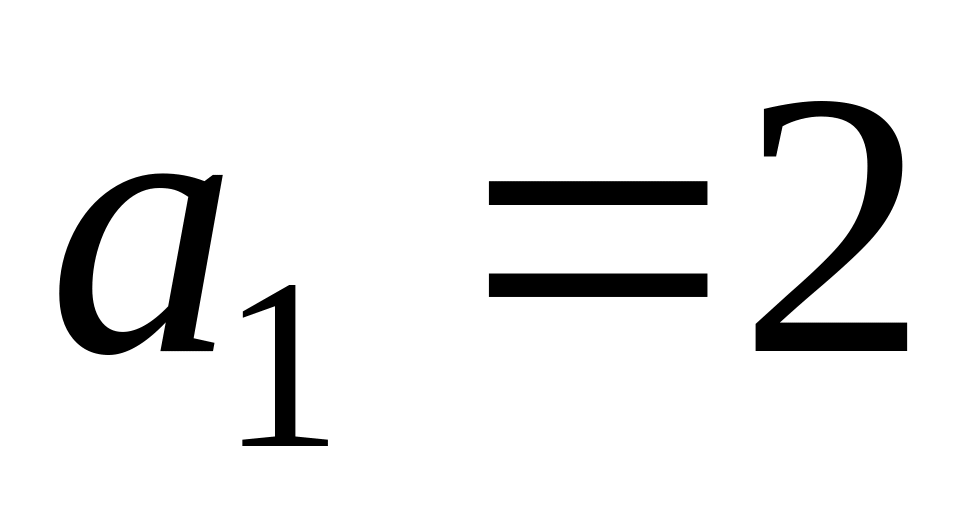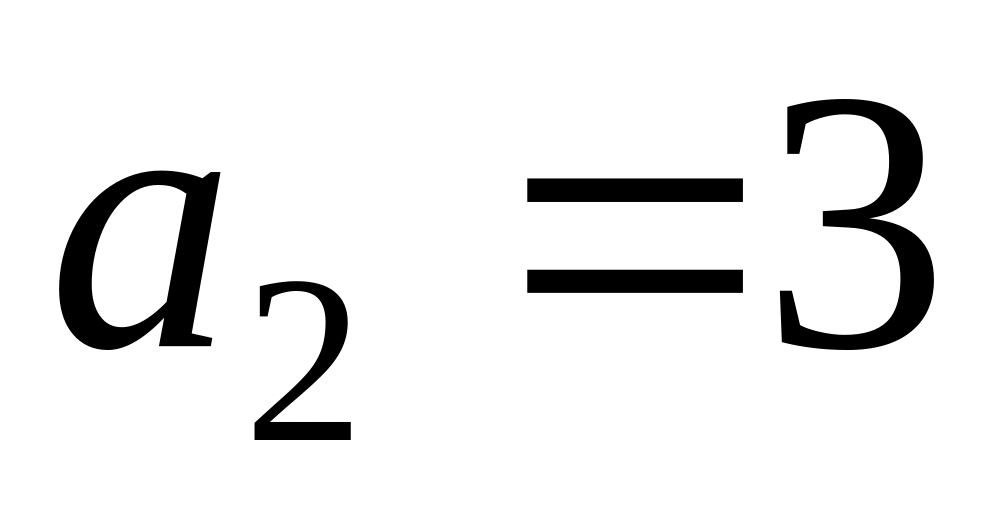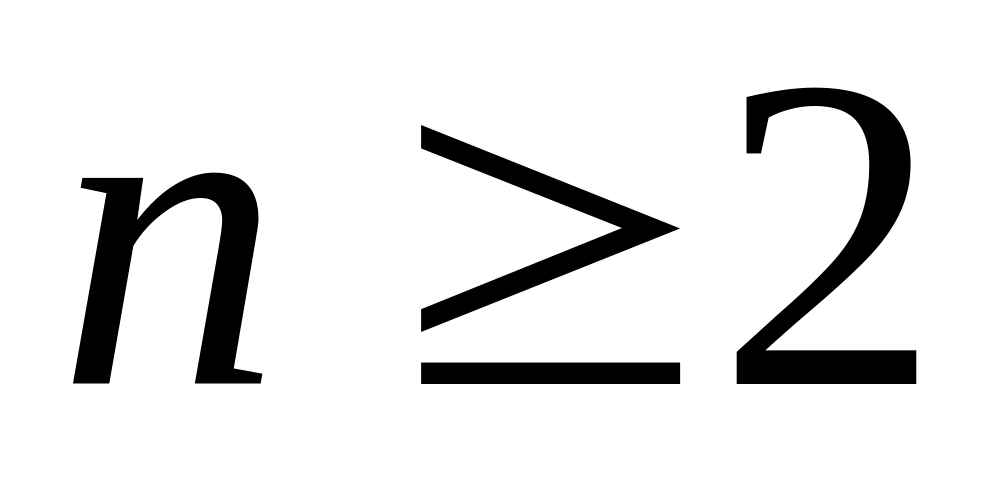Доказать, что
для
Решение. Обозначим
значения а, находимые по предполагаемой
формуле
через
при
.
n=1
(по условию)
(и).
Предположим, что
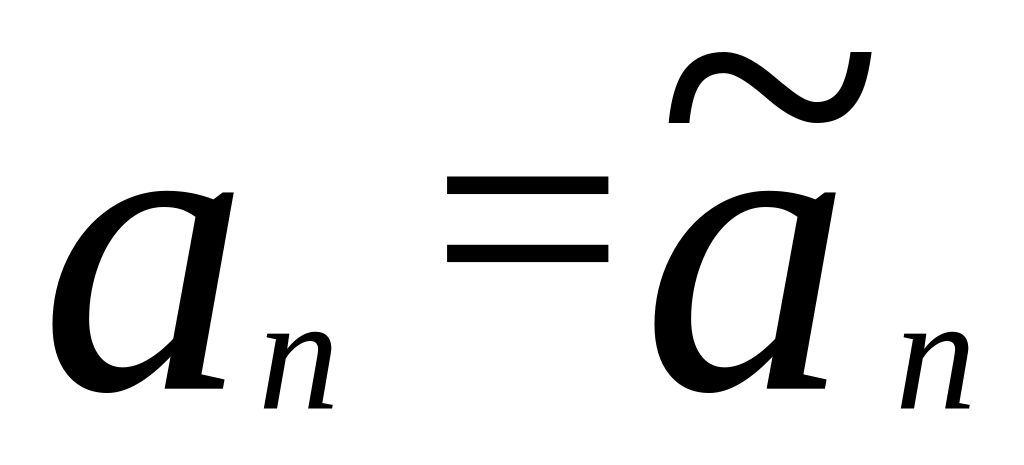для всех значений
от 2 до
включительно (k-произвольное
натуральное число). В частном.
,
,
т. е.
Найдем
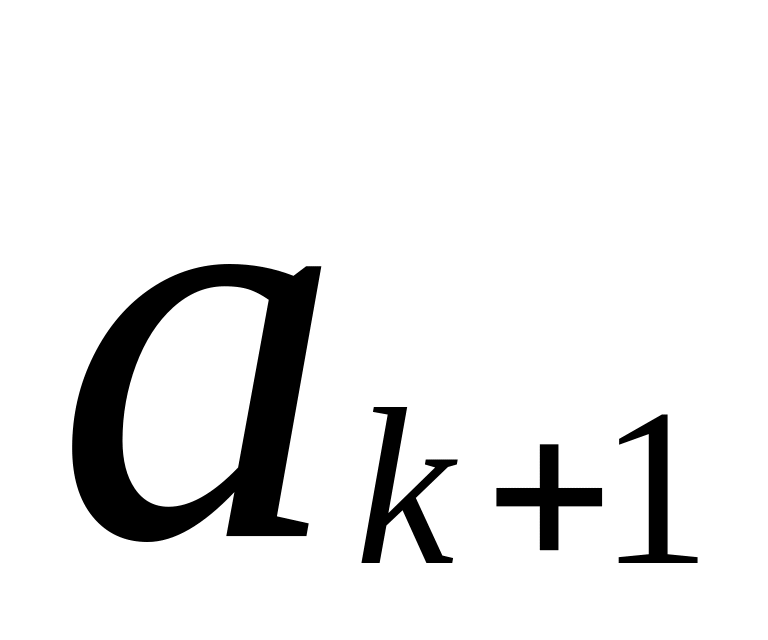и
=
Согласно методу
математической индукции делаем вывод:
предполагаемое утверждение истинно
для
.