Упражнения

1. Найдите область определения рr₁ р и область значений рr₂ р каждого из следующих отношений, заданных на множестве

А = { 1, 2, 3, ..., 10 } N, и укажите, какими свойствами оно обладает:

1) арв<=>а-в=8;

2) арв<»в=а²;

3) арв<=>ав=12;

4) арв<=>в > а².

2. На множестве А={3, 5, 7, 9, 11 } N задано отношение х > у. Выпишите все пары элементов, находящиеся в этом отношении.

3.Построить граф отношения р: хру <=> х = у + 2 на множестве

{-3,-1,1,2,3,4} Z.

4.На множестве У= { у | у Z , -13 ≤ у ≤ -2 } задано отношение R:

х R у <=> х=2у.

Какие из следующих записей верны:

а) (-6,-3) R, б)(-3,-6) R,

в) (-4,-2) R, г)(-8,-4) R.

5.На множестве М={ -8, -6, -4, -2, 0, 2, 4 } Z( задано значение р:хру<=> число х кратно числу у. Записать множество р, перечислив все его элементы. Принадлежит ли р пара (-4, -4)? Найти р(2), р(-8), р(0). Найдите р ^-1(4), р ^-1(-6), р ^-1(0). Что значит отношение х у? Найдите (-4), (-2).

6.Дано множество числовых выражений . Построить граф этого отношения « меньше, чем» на этом множестве.

7.Множество М членов семьи Смирновых состоит из отца Ивана Михайловича, матери Елены Андреевны и четырёх детей: Миши, Тани, Васи и Оли. Между членами семьи существуют отношения родства, которые можно выразить словами: “быть мужем”, “быть братом” и т.д.

а) Укажите всевозможные отношения на множестве М.

б) Записать отношения «быть дочерью» с указанием всех его элементов и построить граф этого отношения.

в) Построить графы отношений «быть братом», «быть матерью».

8. На рис. 3 изображен граф отношения «а брат в» на множестве детей нашего двора { А, Б, В, Г, Д, Е, Ж, 3, И }. Кто из них является мальчиком? Кто девочкой? О ком нельзя по этому графу ничего сказать?

Рис. 3

Индивидуальное задание.

На множестве N для каждого из следующих отношений найдите область определения рr ₁ р и область значений рr ₂ р и укажите какими свойствами оно обладает:

1) хру НОД(х,у)=1; 2) хру у<2х;

3) хру х=у²; 4) хру х≤у;

5) хру у-х=12; 6) хру |у-х|=12;

7) хру (х-у):3; 8) хру ху=30;

9) хру х<у+1; 10)хру у=2х+1.

Задания для самоконтроля.

1. Пусть р и σ отношение эквивалентности на множестве М. Докажите или опровергните , что р σ и р σ- есть отношение эквивалентности.

2. Известно, что отношение р – отношение эквивалентности. Дополните граф этого отношения.

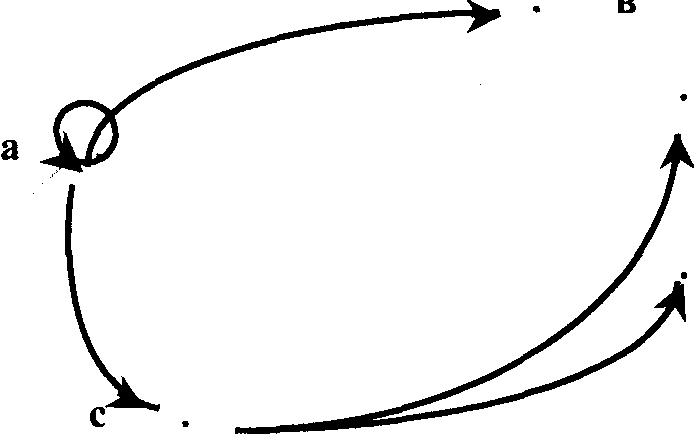
Лабораторная работа №7. Разбиения и их связь с бинарными отношениями

Вопросы к работе.

1. Что такое разбиение множества?

2. Как построить разбиение по данному отношению эквивалентности?

Образцы решения заданий.

1. Пусть . Показать, что подмножества , , образуют разбиение множества .

Решение.

1) Множества , , ;

2) Ø, Ø, Ø;

3) =Ø, =Ø, =Ø

4) = А;

По определению система множеств , , есть разбиение множества .

2. Дано множество . На нем задано отно­шение “иметь один и тот же остаток при делении на 3”. Будет ли это отношение эквивалентностью? Если “да”, то получить разбиение множества М по этому отношению эквивалентности.

Решение.

Из арифметики известно, что любое натуральное число при делении на 3 имеет и притом только один остаток, который может равняться 0,1,2.

По условию задачи хру<=>х и у имеют один и тот же остаток при делении на 3.

Это отношение рефлексивно, т. к. хрх ( х имеет один и то же остаток с х при делении на 3); симметрично, т. к. хру=>урх(если х и у имеют один и то же остаток при делении на 3, то у и х имеют тот же остаток при делении на 3); транзитивно, т. к. хру, урz (если х и у имеют один и тот же остаток при делении на 3 и у с z имеют один и тот же остаток при делении на 3. то х и z имеют одинаковый остаток при делении на 3). Значит, указанное отношение является эквивалентностью.

Найдем разбиение множества М по этому отношению эквивалентности.

Для этого из М возьмем любое число. Например, число 5. Найдем остаток 5 при делении на 3. Это 2. Соберем все числа из М, имеющие при делении на 3 остаток 2 в один класс. Обозначим его символом С1₂={ 5,8,2 }. Число 7 (например) в этот класс не входит. Найдем остаток при делении 7 на число 3. Это 1. Соберем в один класс С1₁ все числа из М, которые при делении на 3 имеют остаток 1: С1₁={ 1,4,7,10}.

Число 3 не входит ни в С1₂, ни в С1₁. Находим остаток при делении и З на З. Это число 0. Составляем класс С1о, куда войдут все числа из М, имеющие при делении на 3 остаток 0: С1о={ 3,6,9 }. Все числа из М распределились по классам С1о, С1₂, С1₁. Другими словами:

1) множества С1о, С1_1, С1₂ M

2) С1о , С1₂ , С1₁ .

3) С1о С1₁ =Ø, С1о С1₂ =Ø _, С1₁ С1₂=Ø

4) С1о С1₁ С1₂ =М.

Итак, искомое разбиение состоит из множеств С1о, С1_1, С1₂